Goldilocks and the Three Rectangles

Est. Class Sessions: 1–2

Developing the Lesson

Part 2: Twins

Wrap up the story and introduce the Twin problem.

The three rectangles thanked Goldilocks for her help. They were all very happy because each of them was the biggest in one way. Goldilocks said good-bye and continued her walk through the woods, keeping a careful eye out for bears, as always.

As the rectangles were returning to their picnic, they heard a crashing sound coming toward them through the forest. Suddenly, another rectangle, Rupert, appeared.

“At last!” Rupert said, “I’ve been searching everywhere. When I was just a small rectangle, I was separated from my twin and have been looking for it ever since.” Rupert exclaimed, “I know one of you is my twin!”

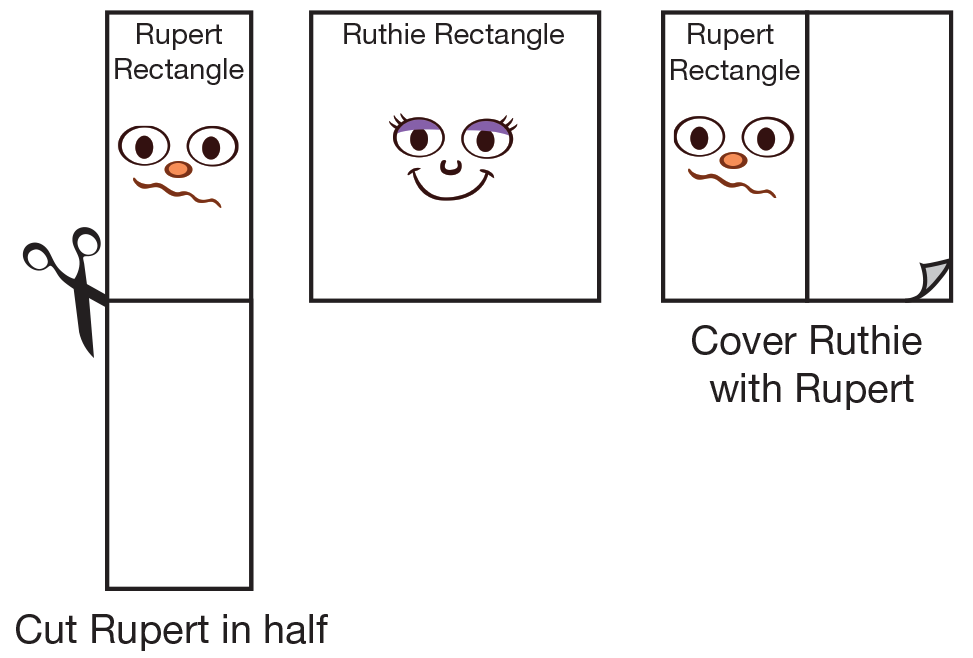
Explain to students that in Rectangle Land, twin rectangles always have the same area although their shapes may be different. Display the page depicting Rupert Rectangle. Have students work in pairs to find ways to identify which rectangle is Rupert’s twin (i.e., which rectangle has the same area as Rupert). Refer students to Math Practice 2, Find a strategy, and have them discuss with their partner good tools and an efficient strategy for solving the problem before they begin. Point out the last row of the Three Triangles Table and tell students to write Rupert’s name in the appropriate column and use this row to fill in Rupert Rectangle’s measurements.

There are a number of ways students can tackle this problem. Some may informally try to compare each shape. Some may cut out Rupert and try to fit him into the area of the others. Others may use the square-inch tiles to obtain an area measurement.

When students are finished, discuss:

What strategies did you use?
Are some strategies more accurate than others?
What is the area of Rupert Rectangle? (16 square inches)
Who has the exact same area? (Ruthie)
Who is Rupert’s twin? (Ruthie)
Look at Rupert and Ruthie together. Do they look alike? (No, Rupert is tall and thin; Ruthie is a square.)
Measure Rupert’s sides using your ruler and compare them to Ruthie’s. What do you notice? (Their side measurements are different.)
Silently decide what you think of this statement, do not answer aloud: Shapes that don’t look alike and don’t have the same measurements can still cover the same amount of space. Close your eyes and signal thumbs up if you agree and thumbs down if you disagree.

Observe students while they complete Check-In: Question 4 on the Goldilocks and the Three Rectangles pages in the Student Activity Book. As they complete the data table for Rupert and find his twin, assess their abilities to measure length in inches [E5]; measure the area of a shape by counting square units noting students’ strategies for counting (e. g., count by ones, skip count rows, etc.) [E6]; and find an efficient strategy to solve the problem [MPE2].

Use class discussion of the activity to assess students’ abilities to recognize that different shapes can have the same area [E4].

To illustrate that the two shapes have the same area, cut out a copy of Rupert and place it on top of a display of Ruthie as shown in Figure 3. Remind students that a square is a special kind of rectangle in which all four sides are equal.