Lesson 4

Unit Designs

Est. Class Sessions: 1–2

Developing the Lesson

Part 1: More Measuring for Goldilocks

Introduce the lesson by telling the following story:

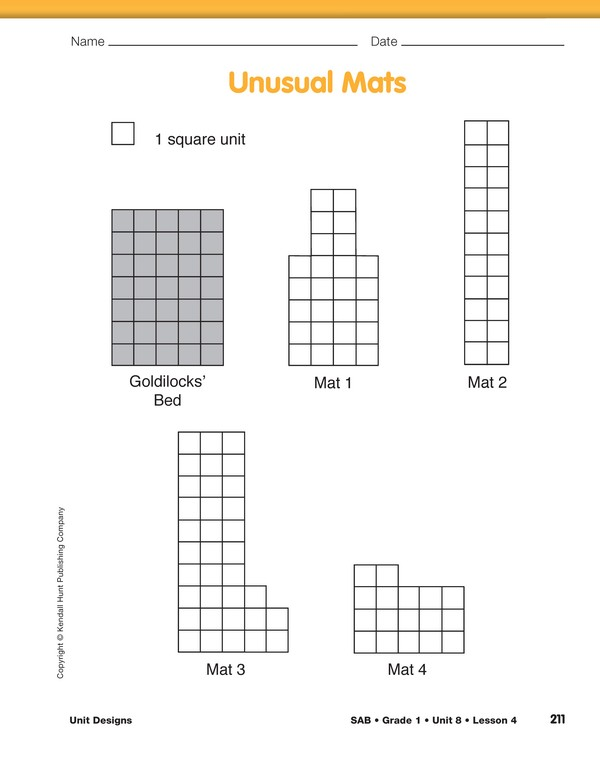
    Goldilocks was walking through the woods again, avoiding both bears and rectangles this time. However, she started to feel sleepy and began to think she needed to take a short nap. She tried to stay awake because she knew she had gotten into trouble when she took a nap at the house of the three bears. She saw a school that had a very unusual shape and decided that she would ask the Kindergarten teacher to let her take a nap on a mat. A very kind teacher answered the door and said, “Of course you may take a nap here. We were just getting ready for a nap ourselves.” She took Goldilocks to the classroom and told her she could pick from the mats of students who were absent. Goldilocks stopped and stared when she saw the four mats. They didn’t look like regular mats at all. They had very weird shapes. It looked like they were different sizes, but she couldn’t tell which was her size because of the strange shapes. Goldilocks knew that her bed at home has an area of 35 square units. She knew that she needed that much space to be comfortable. Help Goldilocks find a mat with the same area.

Introduce Goldilocks’s problem of finding a mat to sleep on by showing the class a display of the Unusual Mats page from the Student Activity Book. Direct students’ attention to Goldilocks’s bed. Encourage students to use skip counting skills and addition strategies to make the task of counting the square units simpler.

Ask:

X
  • How can we make sure that Goldilocks’s bed is 35 square units? (Possible response: We count the square units in each mat.)
  • Since Goldilocks is looking for a mat to use to take a nap, she has to have a mat that is 35 square units. 35 square units is a lot to count. Remember we sometimes get mixed up and lose our place when we have to count high numbers. How can we quickly find the area of each mat? (Possible response: Since her bed has five square units in each row, we can skip count by fives: 5, 10, 15, 20, 25, 30, 35. We can use skip counting for the other mats, too.)

Ask a student to demonstrate skip counting the rows of her bed by fives: 5, 10, 15, 20, 25, 30, 35 square units.

Before asking students to complete the
page, ask:

X
  • Goldilocks knows the three mats are not the same shape as her bed, but she needs to find one with the same area. How will you decide which mat will fit Goldilocks? (Possible response: Find a bed that has 35 square units in it.)

Have students complete the Unusual Mats page in the Student Activity Book independently. Elicit strategies for finding the area of each mat.

See Figure 1 and ask:

X
  • What strategies did you use to make your counting easier? (Possible responses: Use skip counting. Break the mat into parts and count the big part then count on for the rest of the squares.)
  • Why is it easier to count if you divide the shape into parts? (Possible response: You can use skip counting to make it easier and faster to find the total).
  • How can Mat 3 be divided into parts? Is there more than one way to divide it?
  • How can Mat 4 be divided?
  • Which mat is the perfect size for Goldilocks? (Mat 3) How do you know? (Both have the same area,
    35 square units.)
  • Does Mat 3 look like Goldilock’s bed? (no) So can we say that two shapes can have the same area but do not look the same? (yes)
  • What strategy did you use to find the area of Mat 3? (Possible response: I divided it into easy parts. The big rectangle has tens going up and down so I skip counted, 10, 20, 30. Then there was 3, then two, so I count on from 30: 31, 32, 33, then 34, 35.)
  • How could you make another shape that Goldilocks could sleep on?

Give each student pair 35 square-inch tiles and ask them to make a different shape mat for Goldilocks. Have several students share the mat design they created and ask students to show how they know there are 35 square units in their mat.

X

As they divide each shape for counting, students may find it easier to write the number of square units in each section. For example, for Mat 1, after skip counting 5, 10, 15, 20, they write the number “20” in that section of the mat. Then they can count on from that number: 20, 22, 24, 26 square units.

Student Guide:
Student Activity Book: 211
Answers
X
SG_Mini
+
Master:
Strategies for finding the area of the Unusual Mats
X
+