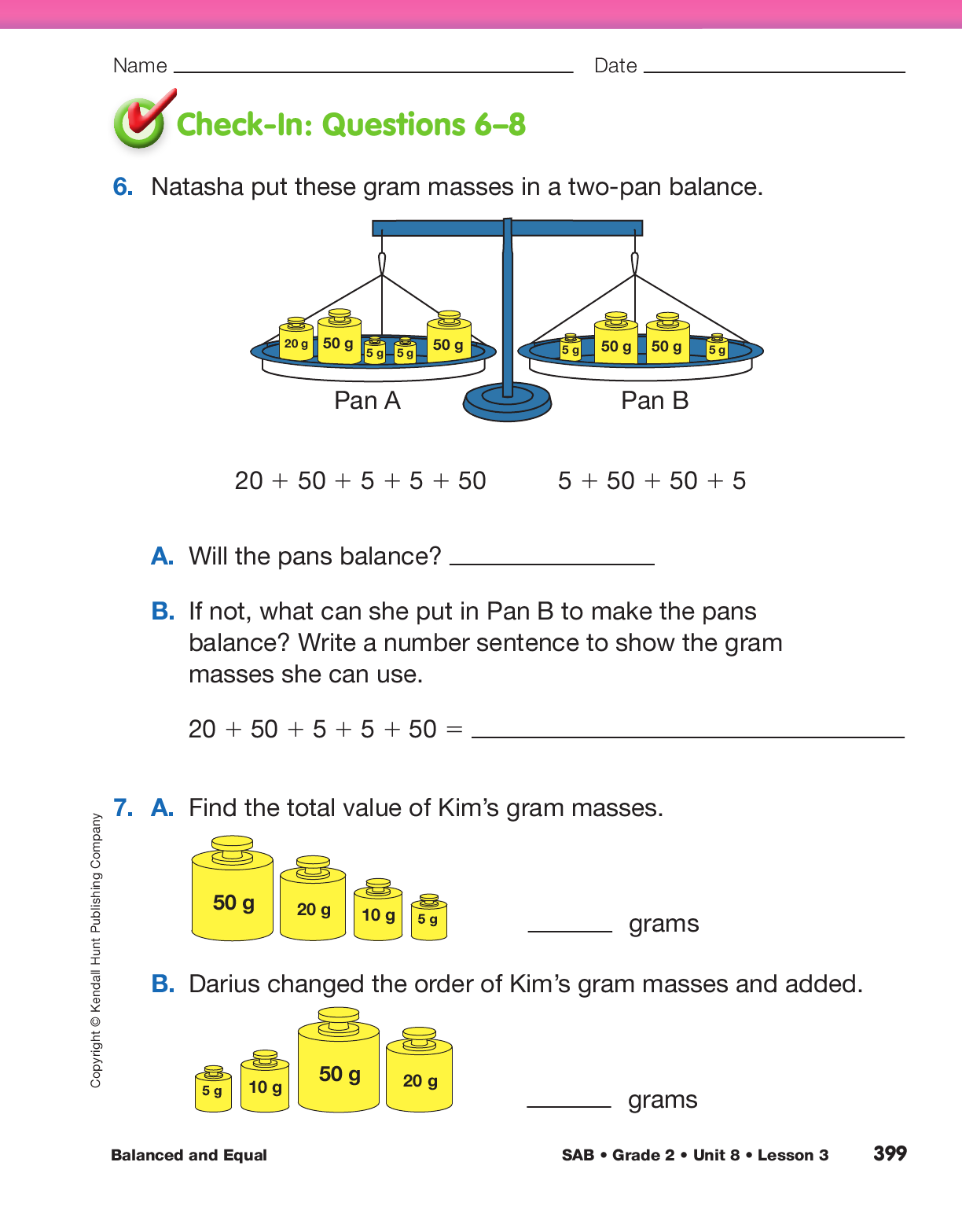
Balanced and Equal

Use Two-Pan Balances to Understand Equivalency. The two-pan balance is a tool that can help illustrate that different partitions of a number are equal. The equal sign in the expression is like a balance. Whatever is on one side of the equation “balances” or equals what is on the other side. To balance the scale, or the equation, something may need to be added or subtracted to one side of the balance, or to one side of the equation.

Display a two-pan balance. Explain that mass is the amount of matter of an object. We can get an idea about the mass of an object by lifting it up. We can use a two-pan balance to measure mass. Explain to students that two-pan balances are similar to seesaws.

If you have not done so already, show students how to zero the balance by making sure the empty pans are level. Explain that this is a balanced scale. Ask students to recall the mice in the Adventure Book story, “The Mouse-Proof Shelf.”

Show students the display set of standard gram masses. In order to measure mass we need a unit of measure. A common metric unit of mass is the gram. To help students understand the abstract idea of balancing expressions, tell them to stand with their arms stretched out to the side and pretend they are two-pan balances. Their hands will be the pans. See Figure 1.

Equations. Remind students that before you can use the balance, you need to make sure it is leveled or balanced. Neither pan can be higher than the other. Demonstrate how to wait until the pans are still. Show students that you are placing a 10-gram mass and one 5-gram mass in one of the pans on the two-pan balance.

Place masses in pan to demonstrate.

Display the number sentence.

Write this response as a number sentence, for example
10 + 5 = 10 + 1 + 1 + 1 + 1 + 1. Ask students to show or tell how they know if it is a true number sentence. Some students may show how the masses in both pans enable the scale to balance. Others may compute, adding the numbers on both sides of the equation to find that the sentence is true. Still others may use the relationship between the expressions on either side of the equal sign to determine whether the number sentence is true. Once students understand that the equal sign means that the quantities on both sides are the same, they can use relational thinking to solve problems. Relational thinking happens when a student uses numeric relationships between the two sides of the equal sign rather than actually computing the amounts. When numbers become larger, this thinking is very useful.

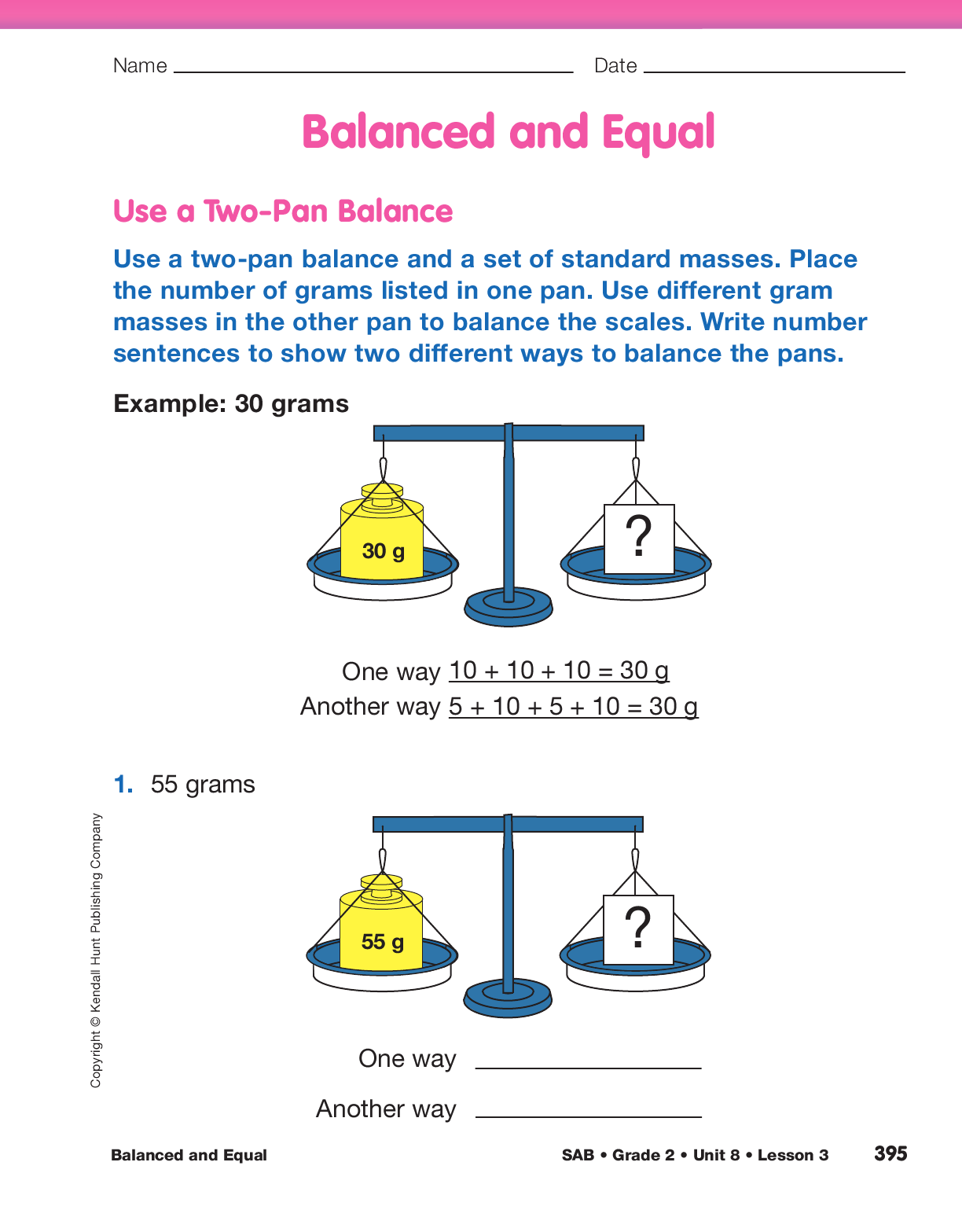
Find Different Ways to Balance a Quantity. Student pairs will use two-pan balances to find different equivalent mass combinations. Before they begin working, it is essential students understand that level pans indicate there are equivalent masses in the pans. Students will place a given amount of mass in one pan. They will add masses to the other pan until the pans balance. If one side is lower, more mass needs to be added to the other pan so that the pans can balance. When the pans are balanced, the masses in the pans are equal.

To clarify, explain to students that you will place a 20-gram and 10-gram mass in one pan. Explain that you will place two 10-gram masses in the other pan.

Explain to students that you are always going to leave the first amount (30 grams) in its pan, and only add or take away masses from the second pan until the scale is balanced. Add too much to the lower pan, for example, another 20-gram mass, to make 40 grams.

Place gram masses in the second pan until the pans are balanced. Display a number sentence that represents the suggested masses, for example, 10 + 10 + 10 = 30. Ask students to explain how they could add the masses.

Leaving 30 grams in the first pan, take all the gram masses out of the other pan.

Display a number sentence that represents the suggested masses, such as 5 + 5 + 10 + 10 = 30. If it has not been demonstrated, show students how to add the larger masses first; for example, 10 + 10 + 5 + 5 = 30.

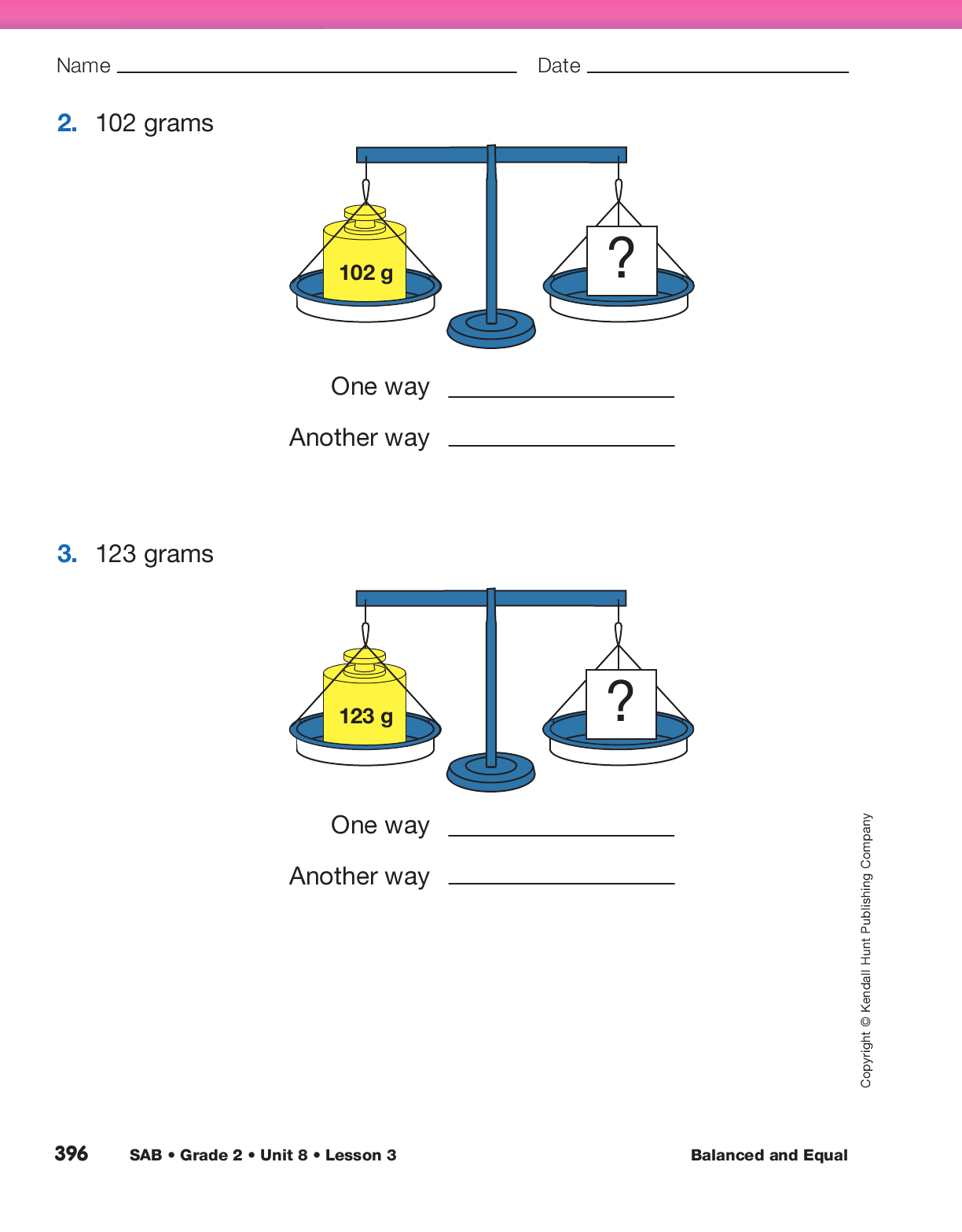
Distribute a two-pan balance and a set of standard masses to each student pair. Again, show students how to zero their balance by making sure the empty pans are level. Direct students’ attention to the Balanced and Equal pages in the Student Activity Book. The example question is similar to the activity you just completed. Use this question to introduce the page and then assign Questions 1–3 in the Use a Two-Pan Balance section. For each question, students should place the number of grams listed in one of the pans. They will then use the other masses to find two other ways to balance the pans. Students will write number sentences to represent the two different combinations of gram masses that they used. Remind them to place the listed number of grams in one pan and then add or take away gram masses from the other pan only until they are balanced.

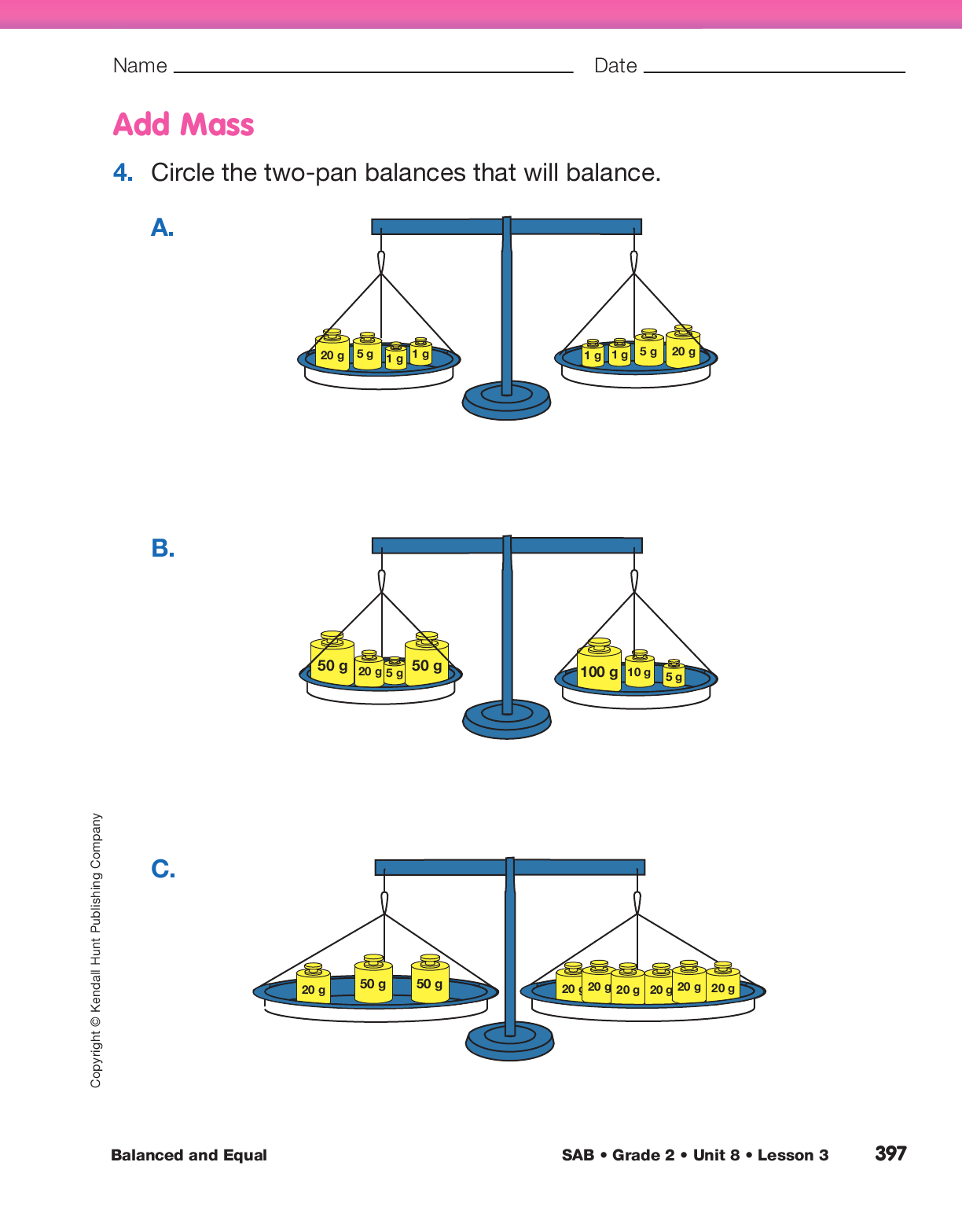
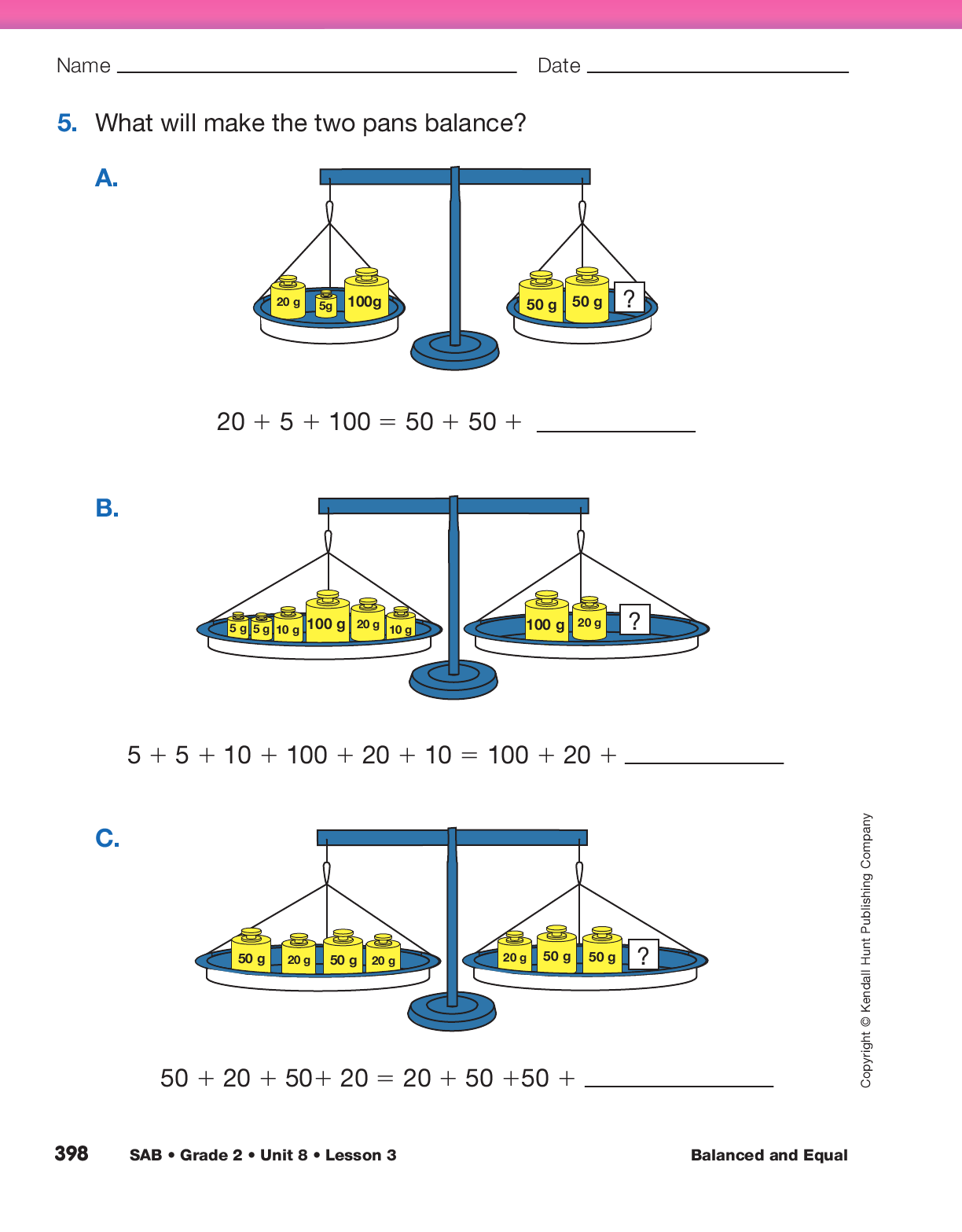
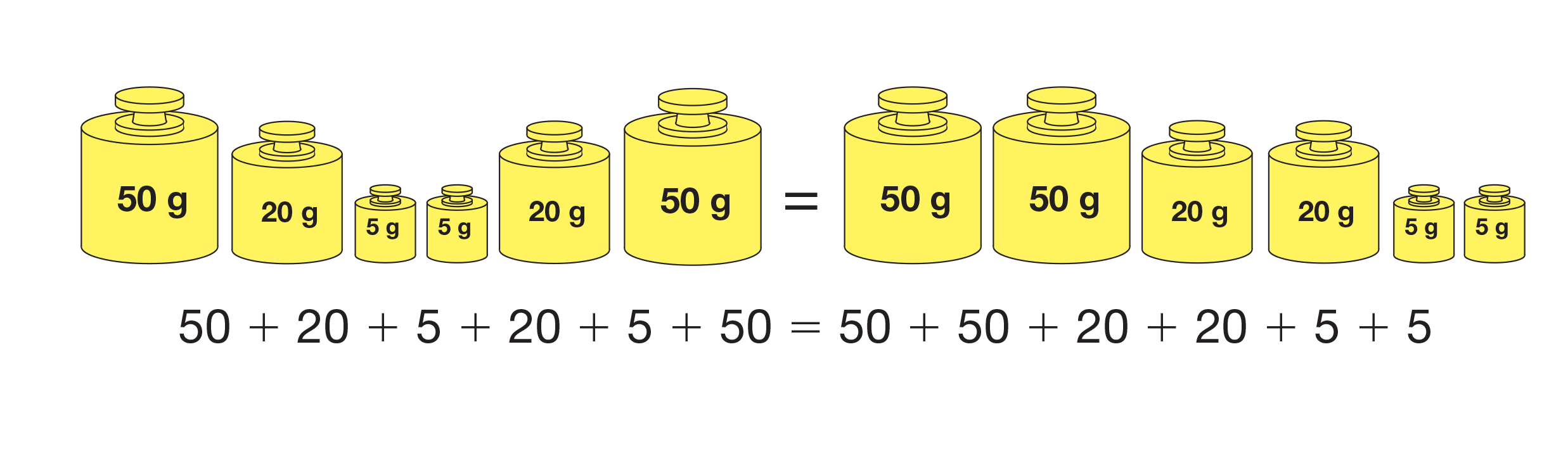
Apply Commutative and Associative Properties. Students do not need to know the terms “commutative property” or “associative property,” but they do need to understand how to apply these important addition properties. The commutative property of addition means that you can change the order of the addends and it does not change the answer. See Figure 2. Although this may seem obvious, it may not be to students.

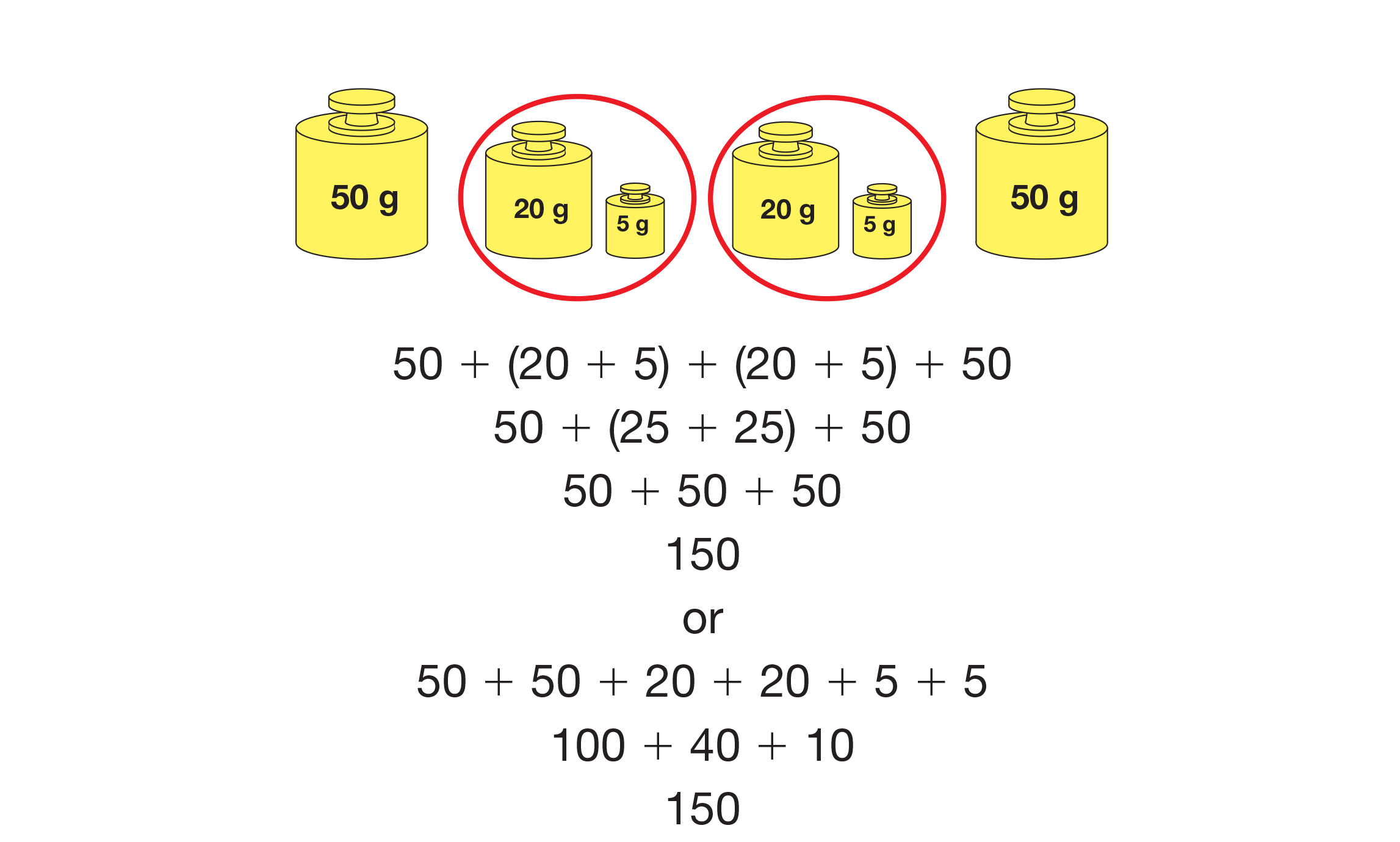
The associative property of addition says that when adding three or more numbers, it doesn’t matter whether the first pair of numbers is added first or if you start with any other pair of addends. Students can change the order in which the masses are grouped to work with combinations that are easier and that make sense instead of just reading and adding the equation from left to right. See Figure 3.

When students have completed Questions 1–3 on the Balanced and Equal pages, display the Natasha’s Gram Masses Master.

As students share the way in which they add the addends, list the number sentences on the Natasha’s Gram Masses Master. Then assign Questions 4–8 in the Add Mass section of the Balanced and Equal pages in the Student Activity Book to provide practice applying the commutative and associative properties of addition.