Geometric Investigations
Area and Perimeter
In this unit, students review basic geometric ideas and explore patterns through geometric investigations. They focus on both rectangular and irregular … read more
Area and Perimeter
In this unit, students review basic geometric ideas and explore patterns through geometric investigations. They focus on both rectangular and irregular polygons and explore three attributes: perimeter, area, and side length.
The word perimeter is Greek in origin, and comes from two Greek words: peri (meaning around) and metron (meaning measure). Perimeter is a measurement of length, so the units of inches or centimeters will be used for perimeter measurements in this unit. Area is a measure of the space within the boundaries of a shape and is measured in square units, e.g., square inches or square centimeters. Students often confuse the perimeter of a shape and the area of a shape. They especially confuse the units of measure. Investigative experiences with area and perimeter will help students differentiate between the two concepts.
The lessons in this unit focus on the meaning and measurement of perimeter and area and on the relationship between them. To find perimeters, students measure the distance around shapes, both by counting methods (using grid squares and tiles) and using rulers. Students using Math Trailblazers have had many experiences finding area. They began by counting square units in kindergarten and first grade. In grade 2, they counted 1/2-square units and 1/4-square units, as well. In grade 3, students estimated the areas of irregular shapes by combining fractional parts of square units.
Counting strategies emphasize the meaning of area and perimeter but are inefficient. In this unit, students will start to develop more efficient strategies for measuring area and perimeter of a shape. Students move from the less-efficient strategies by solving similar problems and looking for patterns in their repeated calculations.
Patterns and Relationships
In Lesson 2 Perimeter vs. Length Lab, students conduct a TIMS Laboratory Investigation of the relationship between the side length of a rectangular … read more
Patterns and Relationships
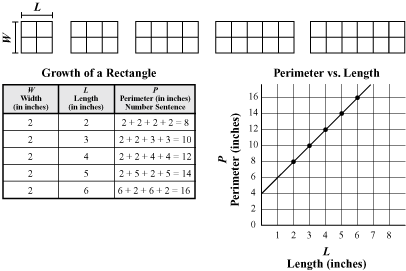
In Lesson 2 Perimeter vs. Length Lab, students conduct a TIMS Laboratory Investigation of the relationship between the side length of a rectangular shape of a given width and its perimeter. Students look for growth patterns as they collect and organize data. For example, Figure 1 shows how the perimeter of a rectangle of a fixed width of 2 inches grows as length is added to the rectangle. Students analyze this growth in the lab using similar tables and graphs.
In Lesson 4 Helipads for Antopolis, students analyze the relationship between area, perimeter, and side length more deeply, again using concrete models, data tables, and graphs. In this activity, students use square-inch tiles to investigate the different shapes and perimeters that are possible for a given area. By using trial-and-error methods and finding patterns in measured data, students find the maximum area for a shape enclosed by a given perimeter. Describing the relationships in these different representations develops a deeper understanding of the concepts and the relationships.
ALGEBRA in the EARLY GRADES

Algebra
Even though this unit is titled Geometric Investigations, it is as much about algebra… read more
Algebra
Even though this unit is titled Geometric Investigations, it is as much about algebra as it is about geometry. Students' investigation of length, perimeter, and area of polygons is not simply an exercise of counting and computing units and square units. Rather, the investigation is a study of change and how it occurs. Students analyze how changing one variable (length) causes a change in another variable (perimeter) while holding a third variable (width) constant. They collect and graph data and then compare their graphs. From their investigations, students develop generalizations that can be applied to similar problems involving perimeter and area. Studying change in related variables and making generalizations from patterns in data involve Algebraic reasoning. For more information on the Algebra Key Ideas in this unit, see the Key Mathematical Ideas and Expectations in the Assessment in this Unit section and the Key Assessment Opportunities Chart.
MATH FACTS and MENTAL MATH

Subtraction Facts
In this unit, students review and are assessed on their subtraction facts. Students… read more
Subtraction Facts
In this unit, students review and are assessed on their subtraction facts. Students have been developing strategies for solving the addition and subtraction facts since their early years and should have gained fluency. See the Letter Home for more about how the facts are grouped by strategy. Unit 3 begins a systematic review of the multiplication and division facts.
Resources
- Charles, Randall. “Big Ideas and Understandings as the Foundation for Elementary and Middle School Mathematics.” Journal of Mathematics Education Leadership, 7 (3), pp. 0–24, 2005.
- Dacey, L., and J.B. Lynch. Math for All: Differentiating Instruction Grades 3–5. California: Math Solutions Publications, 2007.
- Guskey, T.R., and J.M. Bailey. Developing Grading and Reporting Systems for Student Learning. California: Corwin Press, Inc., 2001.
- Jorgensen, M. “Assessing Habits of Mind: Performance-Based Assessment in Science and Mathematics.” Eric Clearinghouse for Science, Mathematics, and Environmental Education, 1994.
- Krulik, S., and J.A. Rudnick. Assessing Reasoning and Problem Solving: A Sourcebook for Elementary School Teachers. NJ: Allyn and Bacon, Pearson, 1998.
- Murray, M., with J. Jorgensen. The Differentiated Classroom: A Guide for Teachers, K–8. Portsmouth, NH: Heinemann, 2007.
- Mathematics Assessment: A Practical Handbook For Grades 3–5. J.K. Stenmark and W.S. Bush, Eds. National Council of Teachers of Mathematics, Reston, VA, 2001.
- Pellegrino, James W. and Susan R. Goldman. “Beyond Rhetoric: Realities and Complexities of Integrating Assessment into Classroom Teaching and Learning.” In C. Dwyer (Ed.) The Future of Assessment: Shaping Teaching and Learning. Mahwah, NJ: Erlbaum, 2007.
- Principles and Standards for School Mathematics. National Council of Teachers of Mathematics, Reston, VA, 2000.
- Tomlinson, C.A. How to Differentiate Instruction in Mixed-Ability Classrooms. 2nd Ed. Association for Supervision and Curriculum Development, 2001.
- Van de Walle, J.A. and L. Lovin. Teaching Student Centered Mathematics: Grades 3–5. Pearson Education, Boston, 2006.











