Helipads for Antopolis

Est. Class Sessions: 2

Developing the Lesson

Part 2: Designing Helipads

Investigating a Small Helipad. Turn to the Helipads for Antopolis pages in the Student Guide. Read and discuss Questions 1–3 together as a class. Explain that a helipad is a surface designed to safely land helicopters. Helipads are often outlined with lights so that pilots can see them when landing at night.

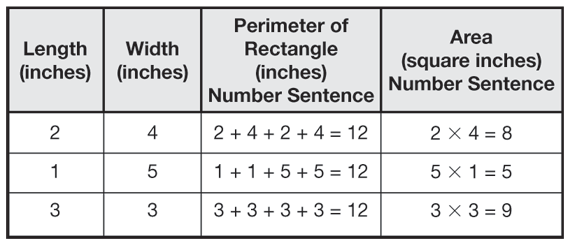
Questions 1 and 2 ask students to find the area and perimeter of the 4-inch by 2-inch helipad shown on the Student Guide page. The area is 8 square inches and the perimeter is 12 inches.

Challenge the students to use the square-inch tiles to find as many rectangles as possible with a perimeter of 12 inches (Question 3A). Have students display the rectangles for the class. Using the square-inch tiles, there are two more rectangles that can be constructed that have a perimeter of 12 inches: 1 inch by 5 inches and 3 inches by 3 inches.

Ask students to show how they found the area and perimeter of each helipad. Some students will count square inches to find area and count units (inches) around the rectangle to find perimeter. Point out to students that they are counting each line that is an inch long when they are finding perimeter. Other students will add the side lengths. Record each strategy as a number sentence. For example, 4 + 4 + 2 + 2 = 12 inches. Have a student use a ruler to measure the length of each side to verify the calculations.

Ask students for suggestions about how to organize the information. A student may suggest a table. Ask the student to make such a table on the board or other class display. See Figure 1.

Ask:

How do we know we have all the possible rectangles with a perimeter of 12 inches? (Possible response: Since we have 1, 2, and 3 inches in the length column, if we go to 4 inches, the width would have to be 2, and we already have that rectangle.)
Do you see any patterns in the table?
(Possible responses: As the length increases by 1, the width decreases by 1. The sum of the length and width is always 6 inches, which is half the perimeter.
Length × Width = Area.)

Discuss Question 3C and accept all answers. Question 3C encourages students to think about the reasonableness of their answers in the context of the specific needs of the initial problem. Here, there is more than one mathematically correct answer. Therefore, the students must think through why one helipad shape may work better than another and give reasons for their choices. This question will also prepare them for their explanations in Question 4E.

Encouraging students to write number sentences to find perimeter and area helps them generalize a formula.

Designing Larger Helipads. Students should now be ready to answer Question 4. Read the paragraph that precedes Question 4.

Ask:

What is Myrna trying to do in this problem? (Build a second helipad that is larger than the first one.)
What do you think is the important information in the paragraph? (The perimeter must be 24 inches, it must be a rectangle, and it needs to be made with square-inch tiles.)
Why do you think that information is important? (It tells how big it should be made and that it must fit in the airport.)

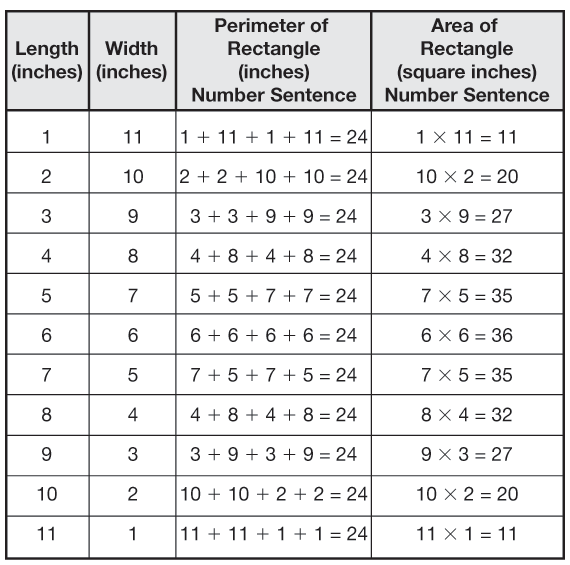
For Question 4, students again work in groups of 2–3 to look for rectangles that have a perimeter of 24 inches. Since we are restricted to square-inch tiles, all lengths and widths must be whole numbers. There are six possible distinct rectangles, displayed in Figure 2.

Question 4C reminds students to keep track of their data in a table as they investigate different rectangles. Allow them to develop their own organizational schemes without showing them the organization of Figure 2. Ask students to describe how they organized their data as they work.

Remind students to label their measurements with correct units—inches for width and length, square inches for area.

Encourage students to explore their data and look for patterns in order to be sure they found all the possible helipads. As students identify a pattern in their data, ask them to explain it to their group members. Some patterns that students may recognize in their data are described here:

Students may realize that the more compact the rectangle—that is, the more square-like the rectangle—the greater the area.
Students may notice that the sum of the length and width in each of their rectangles is 12 inches (one-half the perimeter). Knowing that this sum is 12 inches in every case may help them know when they have found all the rectangles.
If students list their rectangles as shown in Figure 2, they may notice that in each succeeding rectangle, the length decreases one inch as the width increases one inch.

Students may choose different methods for testing the perimeter of the shapes they create with the 1-inch tiles. Some may find the piece of wire that was distributed at the beginning of this lesson helpful. Other students may prefer counting out the perimeter of each rectangle, adding the lengths of the four sides, or using other strategies, e.g., finding the length and width and then doubling. It will be useful for students to hear each others' methods.

A closer look at the patterns in the data table created earlier for rectangles with a perimeter of 12 may help students find the largest area for Questions 4D and E. Some questions might be:

What is the perimeter of the rectangles?
Which rectangle has the smallest area?
Which rectangle has the next largest area?
Does the area keep getting larger?
Which rectangle has the largest perimeter?

Find Helipad with Largest Area. Question 4D asks students to compare the helipads they have drawn or constructed to find the rectangle with the largest possible area and a perimeter of 24 inches. The 6-inch by 6-inch rectangle has the greatest area—36 square inches.

Question 4E asks students to explain how they know that their helipad has the greatest possible area. This problem provides an opportunity to observe Math Practices Expectations 4, 5, and 6. Display the Math Practices page in the Student Guide Reference section.

Some questions that may support a useful discussion:

How do you know you found all of the possible rectangles with a perimeter of 24 inches? How can you be sure?
What lengths did you try? What widths?
How can you use pictures, a data table, or symbols to show you have found the largest rectangle?
How should you label each measurement? (inches for length, width, and perimeter; square inches for area)

Discuss Math Practice Expectations 4, 5, and 6 focusing on what students need to keep in mind as they explain their solutions. Record student ideas on a class display. See Figure 3 for a sample list. Students should use these ideas as guides while they write their own explanations individually for Question 4E.

Students should then share and discuss their explanations with a partner. Tell students to give comments to their partners about how well the partner's answers comply with Math Practices Expectations 4, 5, and 6. Ask students to identify at least one positive point about their partner's paper and at least one suggestion for improvement. This will help prepare students for writing their solutions for Questions 5A and B.

Discuss Questions 4F and G with the whole class. Ask students to describe and compare the helipads with the smallest and largest areas.

Ask:

How would you describe the shape of the rectangle with the largest area? (It is a square.)
What about the rectangle with the next largest area? Is that also a square? (No, it is not a square, it is a little flatter.)
How would you describe the rectangle with the smallest area? Is that a square? (No, it is long and skinny, just one inch wide.)
Do you see a pattern as you go from rectangles with a large area to rectangles with a small area? (Yes. As the area gets smaller, the rectangles get longer and flatter or skinnier.)