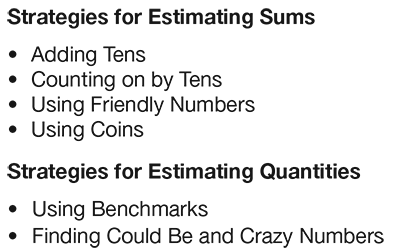Estimation Strategies

Introduce Friendly Numbers. Estimation is very helpful in determining if a solution to a problem is reasonable. Using estimation to find the results of an operation is called computational estimation. Computational estimation usually involves two steps: finding convenient or friendly numbers that make the problem easier and performing the operation on those friendly numbers to find an estimate of the answer.

To introduce the idea of a friendly number, suggest that students think of the number 32. Display and direct students to the 200 Chart in the Student Activity Book Reference section. Tell students that some mathematicians call some numbers “friendly” numbers because they are easier to work with.

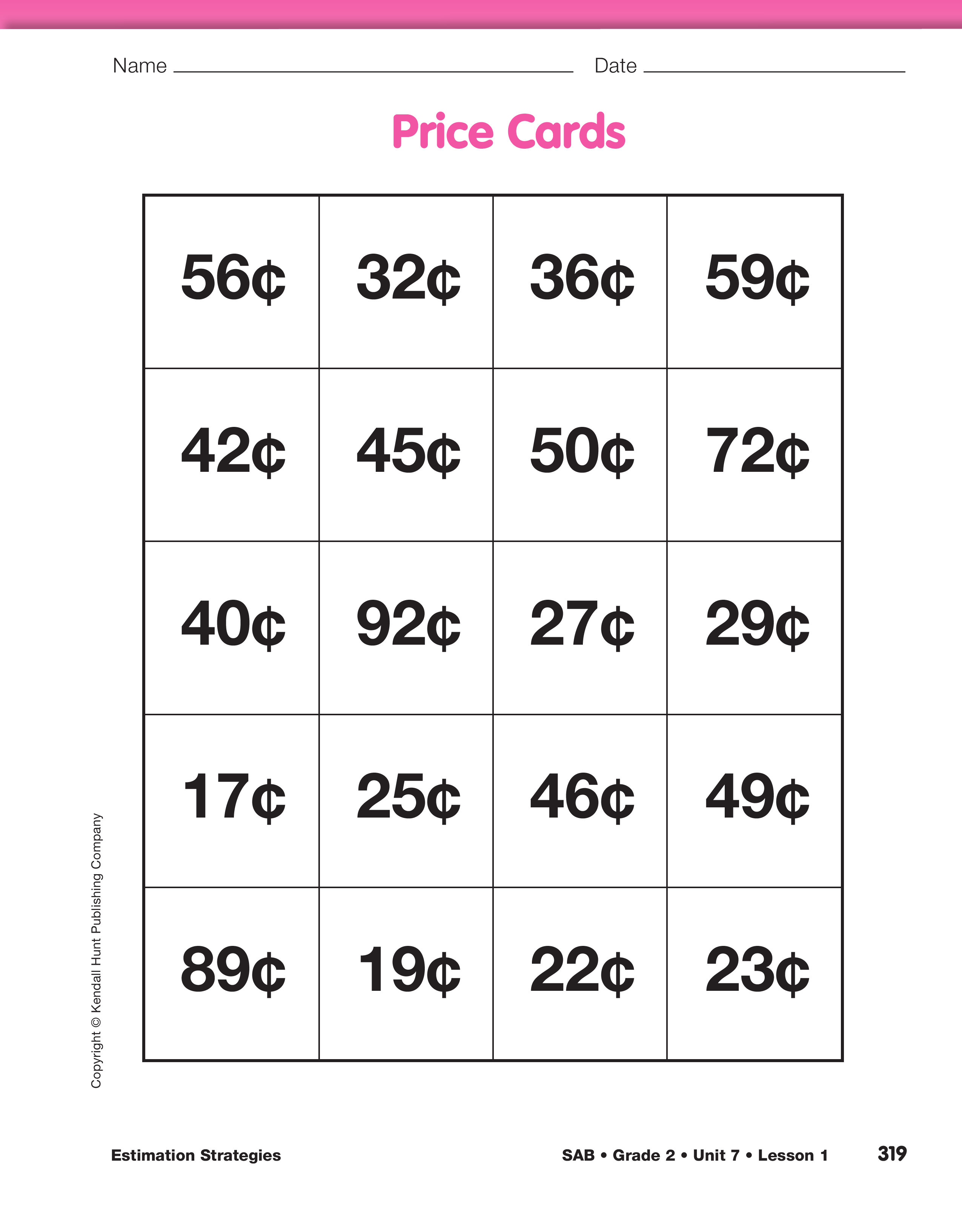
Use Friendly Numbers to Estimate Sums. Display the Price Cards page from the Student Activity Book. Use the price cards to introduce estimating sums. Have a student volunteer choose two price cards and cross them out on the display.

Work through an example by asking the following questions. The answers given are for a 56¢ and a 29¢ card.

Have another volunteer pick two more price cards and cross them out on the display. Ask students to work with a partner to estimate the sum of the two items and tell whether the sum is larger or smaller than one dollar. Tell students to use their 200 Chart to help them find friendly numbers. A similar process can take place on the desk number line, and some students may prefer to find the two closest tens on these rather than the 200 Chart. To discourage students from adding the cards to find the actual sum right away, tell them to be prepared to describe how they estimated. For example, if a 72¢ and a 49¢ card are picked, a student might:

• Look at the tens to see that the sum is more than one dollar: 70¢ plus 30¢ is $1.00, so 72¢ and 49¢ must be more than one dollar.
• Use multiples of ten to skip count for an estimated sum. On the 200 Chart, 72¢ is close to 70¢ and 49¢ is close to 50¢. So, 70, 80, 90, 100, 110, 120; 120¢ or $1.20 is an estimate.
• Use coins to find an estimate of the sum. Students might use quarters: 72¢ is close to 3 quarters (75¢) and 49¢ is close to 2 quarters (50¢); 3 quarters and 2 quarters is 5 quarters. Since 4 quarters is one dollar, 5 quarters would be $1.25.
• Think about tens: 72 has 7 tens and 49 has 4 tens. 11 tens is 110 and more than one dollar.

In all of the examples above, friendly numbers were used to help the estimation process. Friendly numbers tend to be multiples of ten, and, in the case of money, 25 and 75.

Give students some time to share how they estimated the sum. Repeat with another example, encouraging students to use friendly numbers to make estimates.

Direct students to turn to the Price Cards page in the Book. Distribute a calculator to each student pair. Students will take turns doing the following:

• Cross out two price cards on their page.
• Use the 200 Chart or number line to find friendly numbers with which to estimate their sum.
• Tell their partner if one dollar will cover the purchase of one or both items.

The other student will use a calculator to find the sum of the two prices and determine whether the first student is correct. Students switch roles for the next turn. Each student should mark his or her own Price Cards page. Once a card has been crossed out, it cannot be used again. See the Sample Dialog.

Estimate Sums and Quantities. Assign Questions 1–3 on the Estimation Strategies page in the Student Activity Book to partners. An example using friendly numbers is given, but students may use any strategy that makes sense to them. Remind students to explain their strategies for estimating the sum in each problem. As students work, circulate to observe the different strategies they use.

Upon completion, select students to share a variety of estimation strategies. Make a list of the strategies used on chart paper. Have students focus only on the strategies they used to find the sums in Questions 1–3. You will add strategies for estimating quantities next. Ask students to give names to the strategies they used. A student may even want to name his strategy “Mark’s Strategy” which is acceptable. Add strategies for estimating quantities to the class-generated list. Some other possible names of strategies are shown in Figure 2.