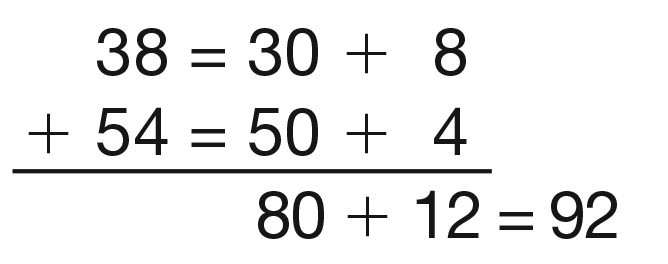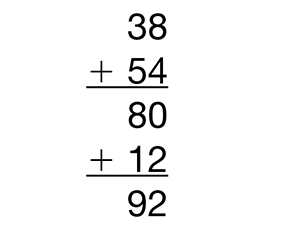Use Base-Ten Pieces. Distribute base-ten pieces to
students. Display the problem 38 + 54. Use a display
set of base-ten pieces to model the two numbers in
the addition problem using skinnies and bits as students
do the same.
Ask questions similar to the following
that make connections between the base-ten
pieces and the symbols in the numbers:
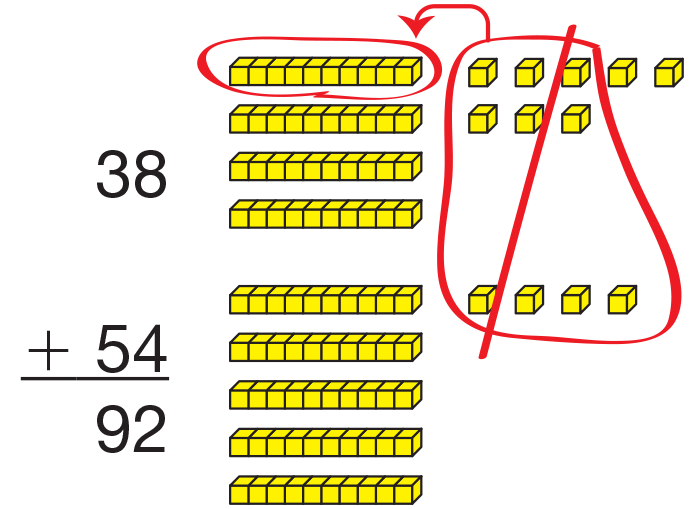
- How did you model 38? (3 skinnies and 8 bits)
- What is the value of the 3 in 38?(Possible responses: 30, 3 skinnies, 3 tens)
- What is the value of the 8 in 38? (Possible responses: 8, 8 bits, 8 ones)
- How did you model 54? (5 skinnies and 4 bits)
- Which of your pieces represents 50? How do you know? (the 5 skinnies; each skinny is a ten, so 10, 20, 30, 40, 50)
- Which of your pieces represents 4? (the 4 bits)
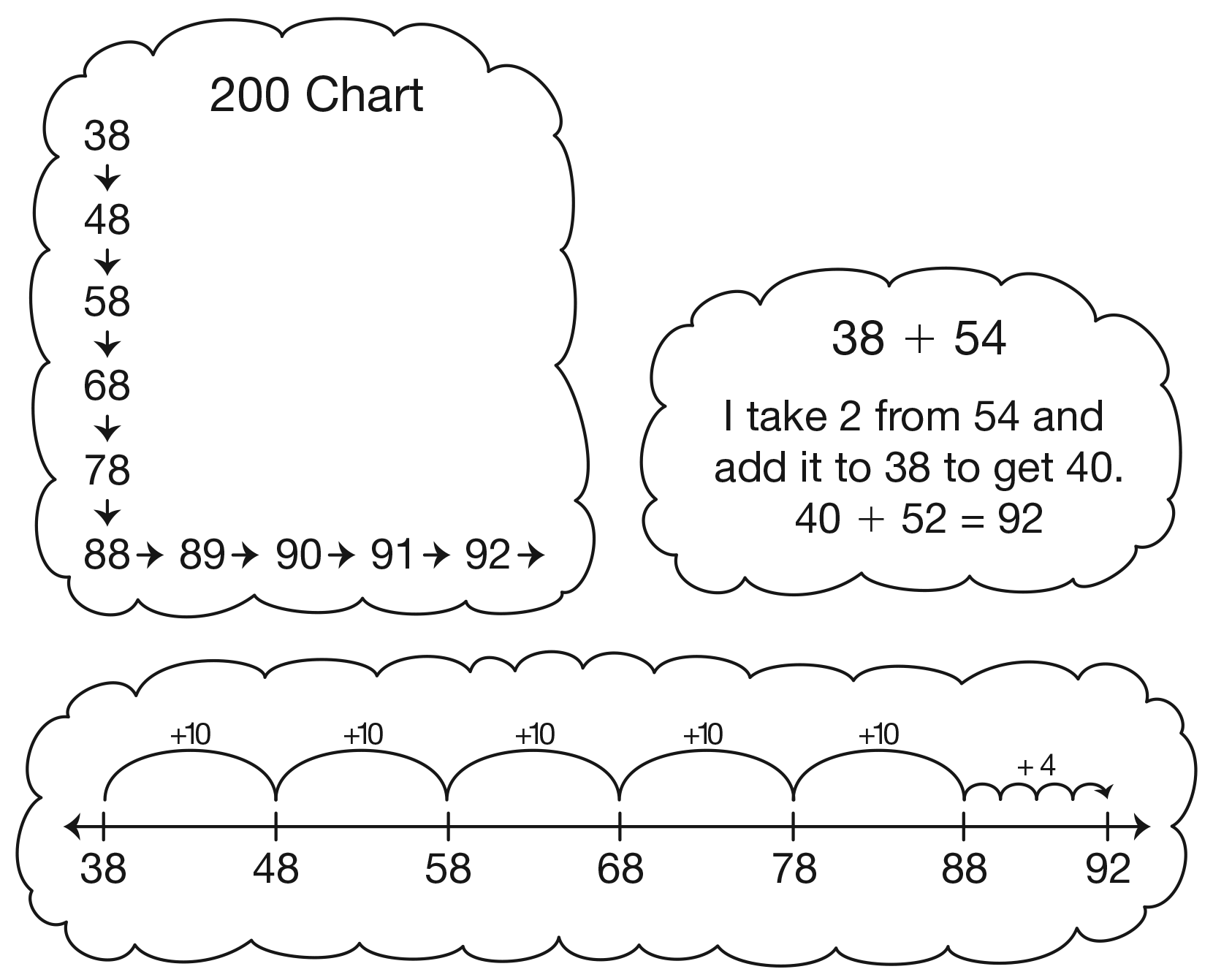
- How can you estimate this sum? (Possible response: I look at my 200 Chart. For 38, the closest ten is 40 and for 54 the closest ten is 50. I estimate a sum of 90.)
- Can anyone use a different strategy to estimate the sum? Explain. (Possible response: I look at the base-ten pieces. There would be 8 skinnies and that is 80. There are 12 more bits and that will make another skinny, so it would be in the 90–100 row of the
200 Chart.)
- Do you think you can make any trades? (Yes, I can trade 12 bits for 1 skinny and 2 bits.)
- Use your base-ten pieces to find the sum of 38 + 54. Remember the Fewest Pieces Rule.
(92; See Figure 1.)
Use Mental Math and Invented Strategies. Display
the Addition Strategies Chart from Lesson 2. Explain
that students are going to solve the same problem in
many different ways so that comparisons can be
made. Tell students to choose one of the strategies on
the chart to use to solve 38 + 54. For example, they
may count on using the 200 Chart or open number
lines. Students also might reason with base-ten
shorthand or money. See Figure 2. As students work,
circulate about the classroom looking for the use of a
variety of strategies. After they solve the problem,
ask several students to display their solution strategies.
Ask questions that make connections between
the strategies such as:
- Show or tell us how you solved this problem.
- Did anyone else use this strategy? Did you get the same answer?
- Did someone use a different strategy from the chart? Explain.
- How did [student name] show 3 tens and 8 ones?
- How did [student name] show 5 tens and 4 ones?
- Which strategy used mental math?
Use Expanded Form and All-Partials. Tell students they are
going to continue to solve the same problem, 38 + 54, but this time they
will use expanded form.
- How can you write 38 to show you have broken it into tens and ones? (30 + 8)
- And 54? (50 + 4)
Tell students to use the expanded-form method to solve the
problem. Have a volunteer display the solution to the class. See Figure
3.
Next, ask the class to use the all-partials method to solve 38 +
54 and have another volunteer display his or her solution. See Figure 4.
- When using the all-partials method, how do you know to add 30 + 50? (The 3 in the tens place means
3 tens or 30. The 5 in the tens place means 5 tens or 50.)
- How did you show that with base-ten pieces?
(3 skinnies plus 5 skinnies)
- How do you know to add 8 + 4? (The 8 in 38 means there are 8 ones and the 4 in 54 means there are
4 ones.)
- Did the order in which you added the base-ten pieces make a difference? Could you add the skinnies first and then the bits? (The order doesn´t make a difference.)
- When you used all-partials, how many of you added the ones first? The tens first?
- When you use all-partials, can you add from right to left or from left to right? (Yes, you can add the ones first or the tens first.)
- Does the order in which we write numbers make a difference? Is 38 the same as 83? How do you know? (Possible response: The order makes a difference. A number has place value. 38 is 3 tens and 8 ones. 83 has 8 tens and 3 ones.)
- What is difficult about expanded form? What is difficult about all-partials?
- Is one strategy quicker than another?
- Is one strategy easier to understand?
- Think about all the strategies we used to solve
38 + 54. Did they all help us find the correct sum of 92? Which one seems to be the most efficient? Why?
Assign Questions 1–4 in the Many Ways to Solve a Problem section
on the Help Them Finish pages in the Student Activity Book. Students
will practice using a variety of methods to solve 2-digit addition
problems.