Estimate Sums of Addition Problems with Trading. Display addition problems with trading,
such as the following, and ask students to estimate
the sum for each problem:
| 48 |
69 |
135 |
182 |
| + 27 |
+ 33 |
+ 127 |
+ 124 |
- What is your estimate for the problem [48 + 27]?
(Possible response: 80)
- What strategy did you use to find your estimate?
(Possible response: I used friendly numbers. 48 is
close to 50 and 27 is close to 30; 50 + 30 = 80.
My estimate is 80.)
- Did anyone use a different strategy? (Possible
response: I added tens. I added 40 + 20 and that
equals 60.)
- Do you think the actual sum is closer to [60] or
[80]? (Possible response: I think it’s closer to 80
because if you add the tens, you get 60, but you
have to add the ones, too. 8 + 7 is 15. If you add
that to 60, the answer is closer to 80.)
Include addition problems with sums to 500 that
involve trading base-ten pieces, such as 135 + 127.
Help students to understand how estimating
135 + 127 is similar to estimating
35 + 27. For
example, to use friendly numbers for 35 + 27, add
40 + 30 = 70. To use friendly numbers for
135 + 127, add
140 + 130 = 270.
Make Trades While Adding with Base-Ten Pieces.
Have students model the problem 48 + 27 using
base-ten pieces. Ask questions that make connections
between the base-ten pieces and the numbers in
the number sentences.
-
How can we use skinnies and bits to model the
number 48 using the Fewest Pieces Rule?
(4 skinnies and 8 bits)
-
How can we model that number using base-ten
shorthand? (4 lines and 8 dots) [Write the
base-ten shorthand next to the number.]
-
How can we use skinnies and bits to model the
number 27? (2 skinnies and 7 bits)
-
How can we model that number using base-ten
shorthand? (2 lines and 7 dots) [Write the
base-ten shorthand next to the number.]
-
How can we write 48 to show we have broken it
into 4 tens and 8 ones? (40 + 8)
-
How can we write 27 to show that we have broken
it into 2 tens and 7 ones? (20 + 7)
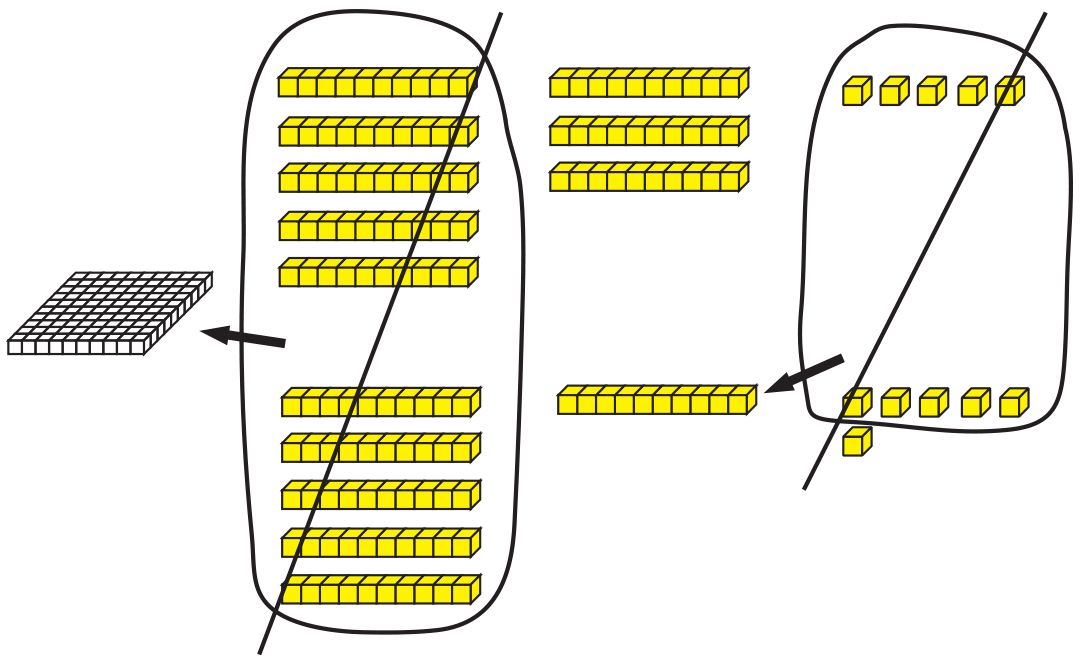
After students use base-ten pieces to model the numbers,
ask them to find the total number of skinnies
and bits. See Figure 2 for possible strategies for
solving 48 + 27.
- How many skinnies and bits do you have?
(Possible response: 6 skinnies and 15 bits)
- Does the answer use the Fewest Pieces Rule?
(Possible response: No, we can make trades.)
- What trades can we make to apply the Fewest
Pieces Rule? (Possible response: We can trade 10
bits for another skinny.)
Demonstrate how to trade 10 of the 15 bits for another skinny.
- How many skinnies and bits do we have now? (7
skinnies and 5 bits)
- Do 6 skinnies and 15 bits show the same number
as 7 skinnies and 5 bits? How do you know?
(Possible response: Yes, because 6 skinnies is 60
and 15 more makes 75.)
Write: 60 + 15 = 70 + 5
- Is this a true statement? Why? (Possible response:
Yes, because 60 + 15 = 75 and 70 + 5 = 75. We
just traded 10 of the 11 bits for another skinny.)
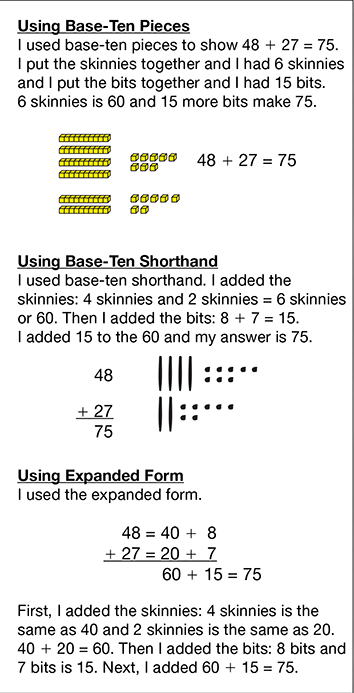
- How can we show trades when we use base-ten
shorthand? (Possible response: We can circle ten
bits and make another skinny.)
- How can we check our answers for reasonableness?
(Possible response: We can estimate by
using friendly numbers: 48 is close to 50 and 27
is close to 30. 50 + 30 = 80. The answer 75 is
close to 80.)
Encourage students to experiment with how to show
the trading step. One suggestion is to circle ten bits
and draw an additional skinny, and then connect
them with an arrow to show that the ten bits were
traded for the skinny. It also suggested that the ten
bits be crossed out so they are not counted again.
See Figure 3.
Ask students to solve additional problems that
involve trading 10 bits for one skinny such as:
67 + 25
37 + 37
49 + 22
Then, pose problems in which students will have to
trade ten skinnies for a flat or make two trades. See
Figures 4, 5, and 6. Figure 6 show how to show two
trades to find the fewest pieces. Give students problems
similar to the following problems:
Ask students to show the problem using their
base-ten pieces and then solve it.
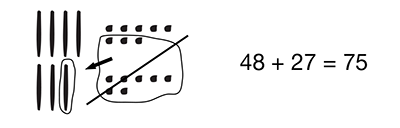
- What is your answer to 85 + 33? (Possible
response: 11 skinnies and 8 bits)
- Can we make any trades? (Possible response: Yes,
we can trade 10 skinnies for 1 flat.)
- How many flats, skinnies, and bits do we have
now? (1 flat, 1 skinny, and 8 bits)
- How is this problem different from the ones we’ve
done before? (Possible response: We don’t have
to trade any bits, but we have too many skinnies.
We have to trade 10 skinnies for a flat.)
- Do 11 skinnies and 8 bits show the same number
as 1 flat, 1 skinny, and 8 bits? How do you know?
(Possible response: Yes. One flat is 100; 1 skinny
is 10, and 8 bits is 8; 100 + 10 + 8 = 118.)
Use the display of the first Trade for Fewest Pieces
page in the Student Activity Book to introduce the
activity and demonstrate the example. Have students
work in pairs to complete the pages. Remind them to
check their answers for all possible trades and record
the trades with base-ten shorthand or a drawing. For
each problem, have students estimate the answers to
check for reasonableness.

For each problem, after students have modeled the numbers
with base-ten pieces and found the sum, ask them to
compare their answer with their estimate to determine
whether their answer is reasonable. Students should begin to
recognize that adding the tens digits works to identify the
precise interval only when no regrouping is required. If the
ones add up to more than ten, thereby necessitating
regrouping, the answer will be in the next higher interval.
This provides one more layer of understanding in upcoming
lessons about what actually happens when they use an
algorithm (paper-and-pencil method) to add.

Observe your students as they build models of the numbers
and write the base-ten shorthand. Some students may
quickly get to the point where they can forego handling the
base-ten pieces themselves and go straight to drawing the
numbers using the base-ten shorthand. Most, however, will
need repeated practice solving the addition problem using
the base-ten pieces first before drawing it with base-ten
shorthand. Make sure these students continue to have the
base-ten pieces readily available.