The Nameless Scribe

Est. Class Sessions: 1–2

Developing the Lesson

Introduce the Story. To begin the lesson, ask students to share their ideas about the symbol zero with the class.

Ask:

Have you ever wondered how or why zero was invented?

Tell students that you will read a story about how zero might have been invented. Note that the true story of the invention of zero is unknown. This story is historical fiction. Some of the elements are plausible (the north Indian setting, the role of scribes, the use of counting boards), but the details are pure fiction.

Choose one student to be a “scribe” as the story is read aloud. Explain to the class that a scribe is a writer. The class scribe will represent and display solutions to problems presented in the story for the class to see. The scribe will need a display set of base-ten pieces.

You can keep the same student as the scribe or assign a new scribe periodically.

When the scribe is ready, write “300208” on the board or display and ask:

The story begins with a little girl named Heather who writes three hundred twenty-eight like this. What’s wrong with writing 328 the way Heather does? (She has too many zeros. She wrote a number that is much larger than 328)
What is the correct way to write three hundred twenty-eight? (328)
Scribe, please use the fewest base-ten pieces to show 328. (3 flats, 2 skinnies, and 8 bits)
Who can tell the scribe a number sentence that matches the shorthand? (300 + 20 + 8 = 328)
How many hundreds do you have? (3) How many tens? (2) How many ones? (8)
How is the partition similar to the way Heather wrote her number? (Heather shows that there is 300 and 20 and 8, too. Both the partition and Heather’s number show all the zeros.)
How is the correct way to write three hundred twenty-eight different from the partition and Heather’s number? (The correct way doesn’t show all the zeros. We know how much the digit stands for because of where it is placed in the number.)

Begin reading “The Nameless Scribe” story aloud.

Page 5

The exact time and place of the invention of the symbol for zero is unknown. It probably took place in northern India about 600 ad. This is the setting for the story Heather’s mother tells.

Page 6

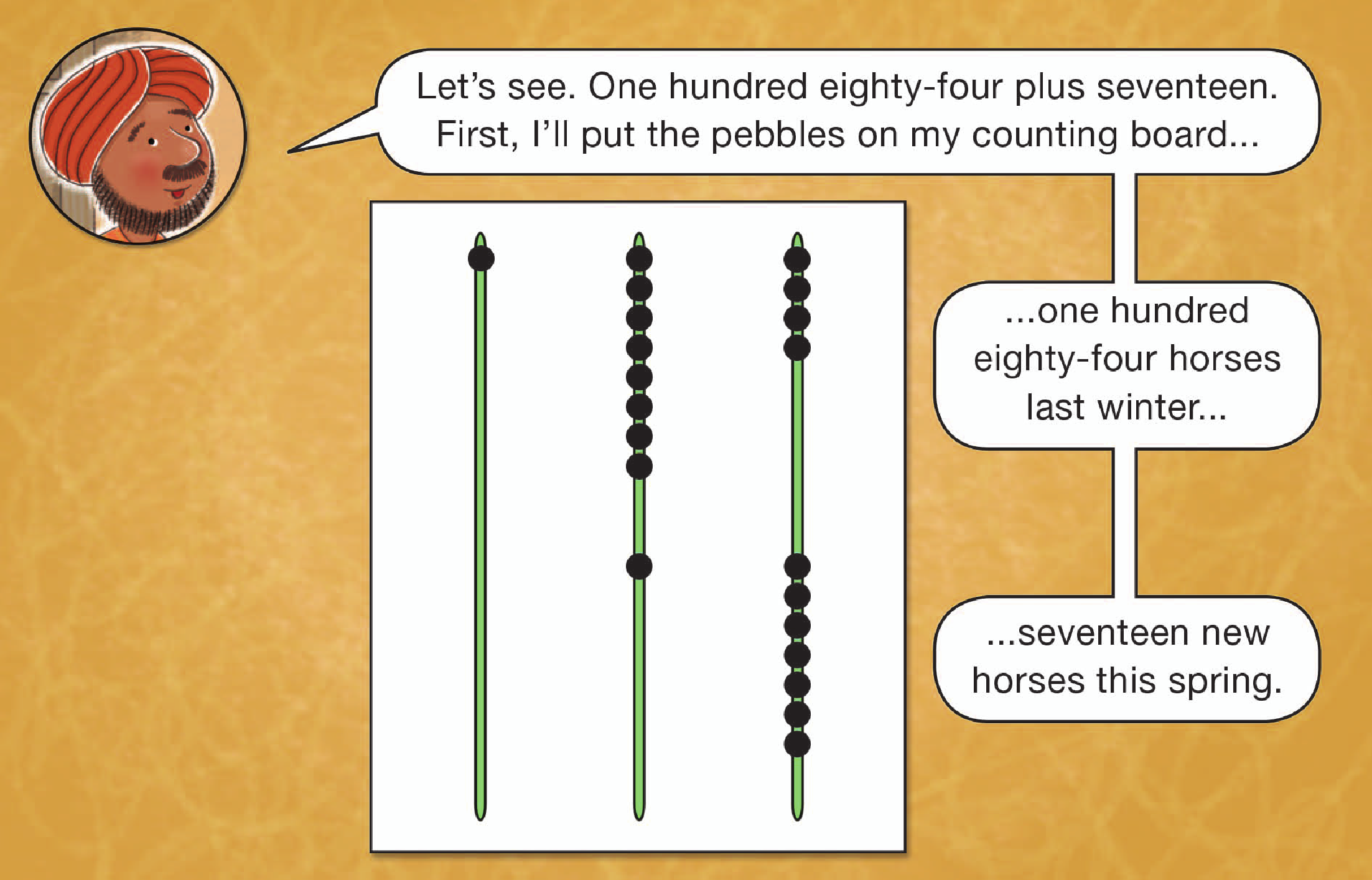
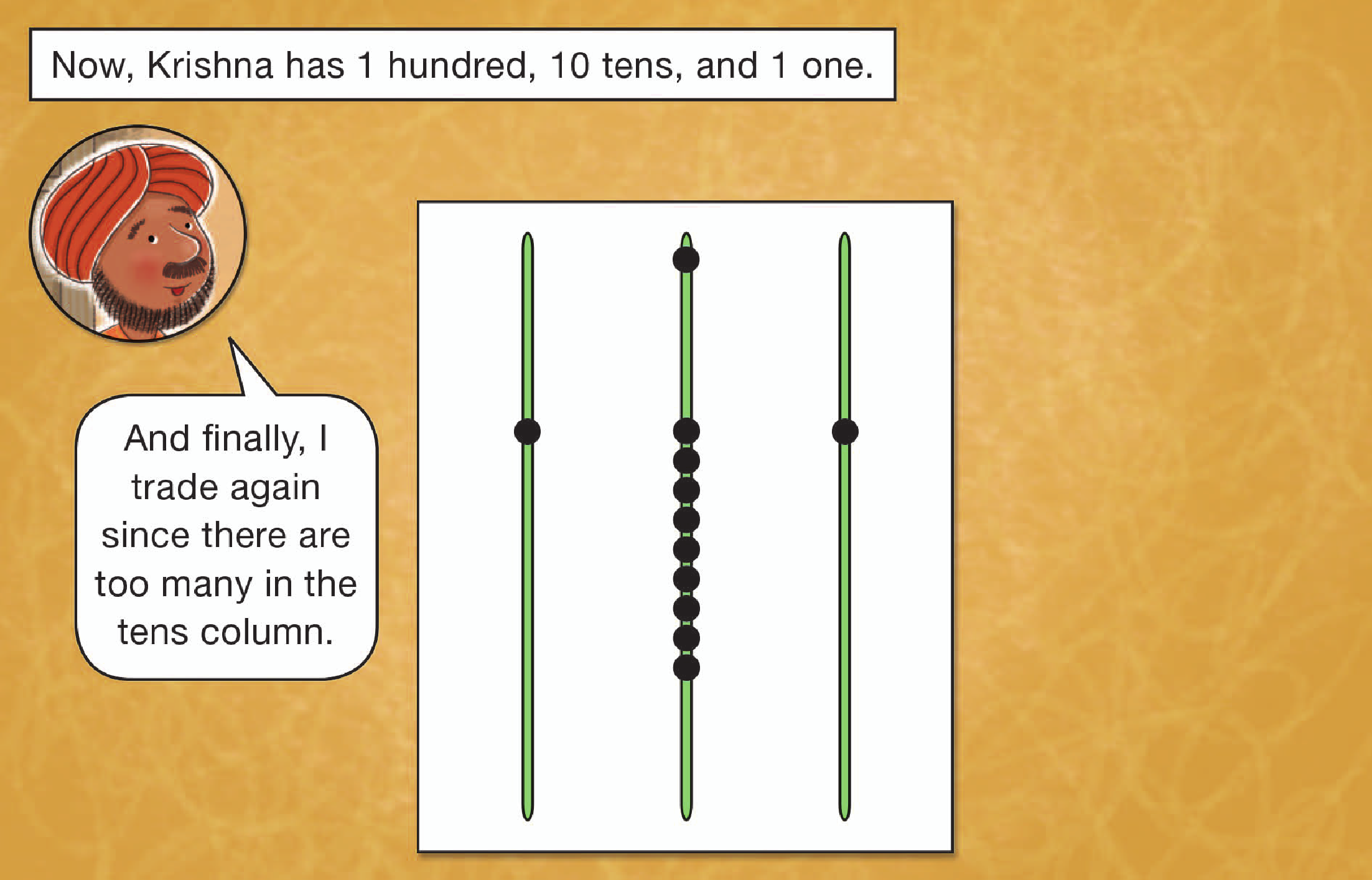
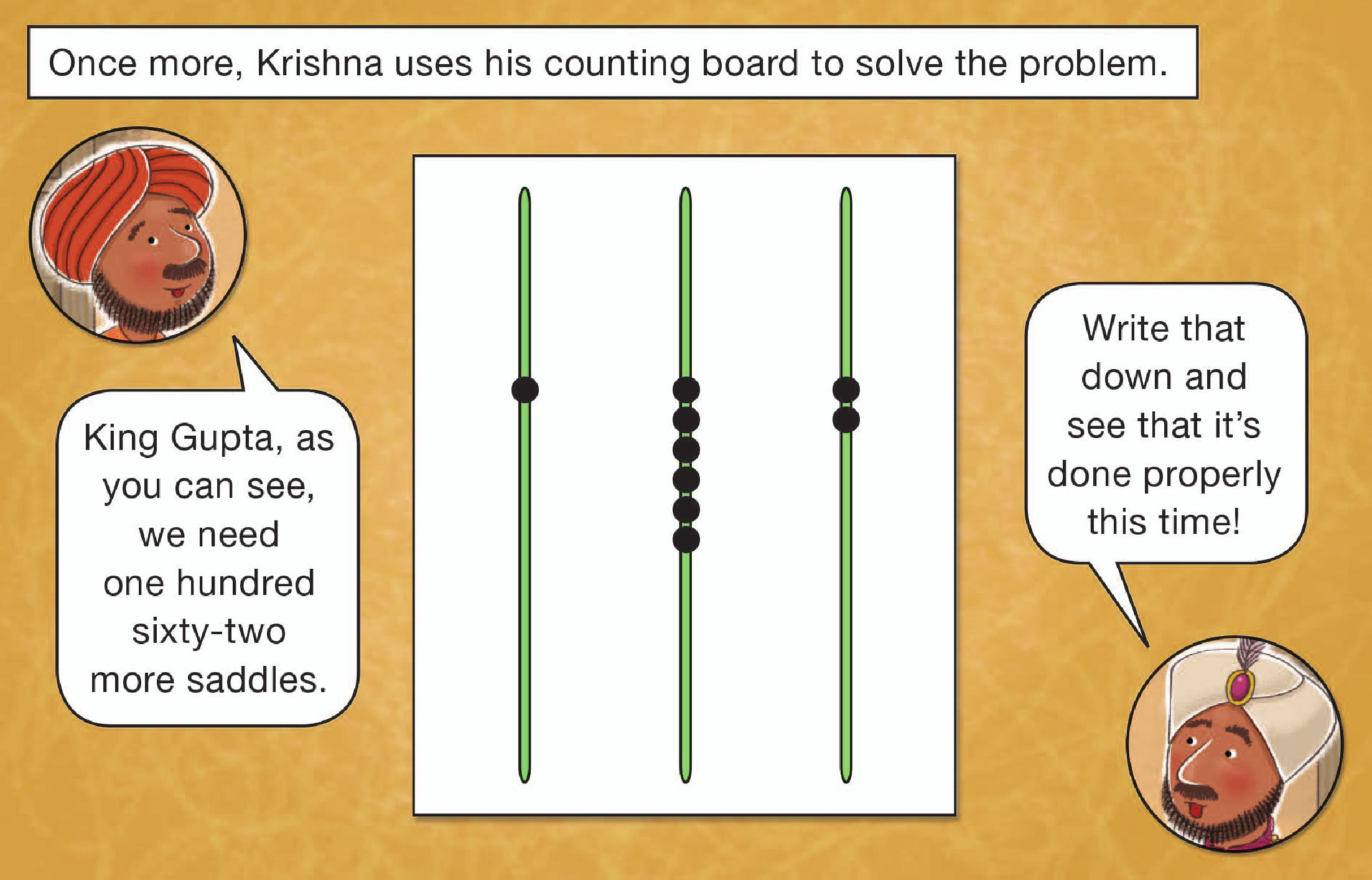
Counting boards like Krishna’s were widely used for computations for hundreds of year. Written symbols were used to record results of work carried out on counting boards.

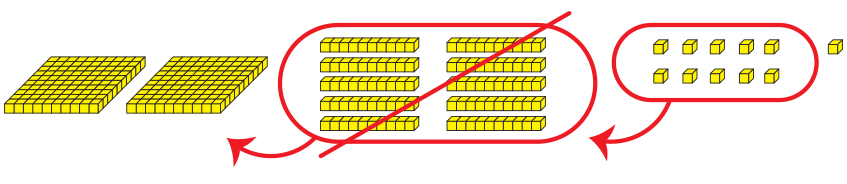
The pebbles on a counting board are not fixed on wires as on a modern abacus, but are removable and fit in grooves incised on the surface of the board. The word counter comes from the custom of building such counting boards into tabletops in stores. Our words calculate and calculus come from the Latin calculi, pebbles, from the use of pebbles on such counting boards. The pebbles on the counting board are all the same size. The same pebble can stand for 1, 10, or 100 depending on which column it is in. The value of a pebble depends on its position, not its size.

Page 9

Ask:

King Gupta had 184 horses. Then 17 more horses were born. How many horses does the king have now? Scribe, can you show and tell us how to solve this using base-ten pieces? (See Figure 1.)
How many flats, skinnies, and bits is that? (2 flats, 0 skinnies, and 1 bit)
Write a number sentence to match. Include a label in your answer so we know what the numbers mean. (184 + 17 = 201 horses)
Krishna made some trades. Did our scribe make any trades? (Yes, the scribe traded bits for skinnies and skinnies for flats like Krishna did with his pebbles.)

Page 10

Ask:

Look how Krishna showed two hundred one. Why did he write it that way? (He wrote “2” for the two pebbles on the hundreds line and “1” for the single pebble on the ones line.)
When we solved the problem using base-ten pieces, we didn’t have any skinnies. How did Krishna show that he didn’t have any pebbles on the tens line? (He left a little space between the 2 and the 1.)
Do you think he will get the right number of saddles? Why or why not? (No, because he only wrote 21.)

Page 13

Ask:

Krishna and the king needed 201 saddles, but only got 21. Scribe, use base-ten pieces to solve
201 – 21 and show how many more saddles they need. Include a number sentence and a label.
(201 – 21 = 180 saddles; See Figure 2.)

Page 14

Ask:

How did Krishna write one hundred-eighty? (18)
180 has how many hundreds? (1) Tens? (8) Ones? (0)
18 has how many hundreds? (0) Tens? (1) Ones? (8)
Do you think the number of saddles will be close to the amount Krishna ordered or not very close? (Possible response: not very close because he forgot one whole hundred)

Page 17

Ask:

They needed 180 more saddles but only got 18. Scribe, use base-ten pieces to solve 180 – 18 and show how many more saddles they need. Include a number sentence. (180 – 18 = 162 saddles; See Figure 3.)
How many flats, skinnies, and bits does the scribe show? (1 flat, 6 skinnies, and 2 bits)
What number sentence describes this partition? (100 + 60 + 2)

Page 18

Ask:

How does Krishna show this number? (162)
Do you think he will have any trouble with this order? Why or why not? (No, I don’t think he will have any trouble because there are no zeros in the number.)

Page 19

Ask:

What do you think will happen when Krishna tries to write the orders for the king’s feast? (Possible response: I don’t think Krishna will order the right amount of items.)
Let’s try placing the orders for the king’s feast ourselves.

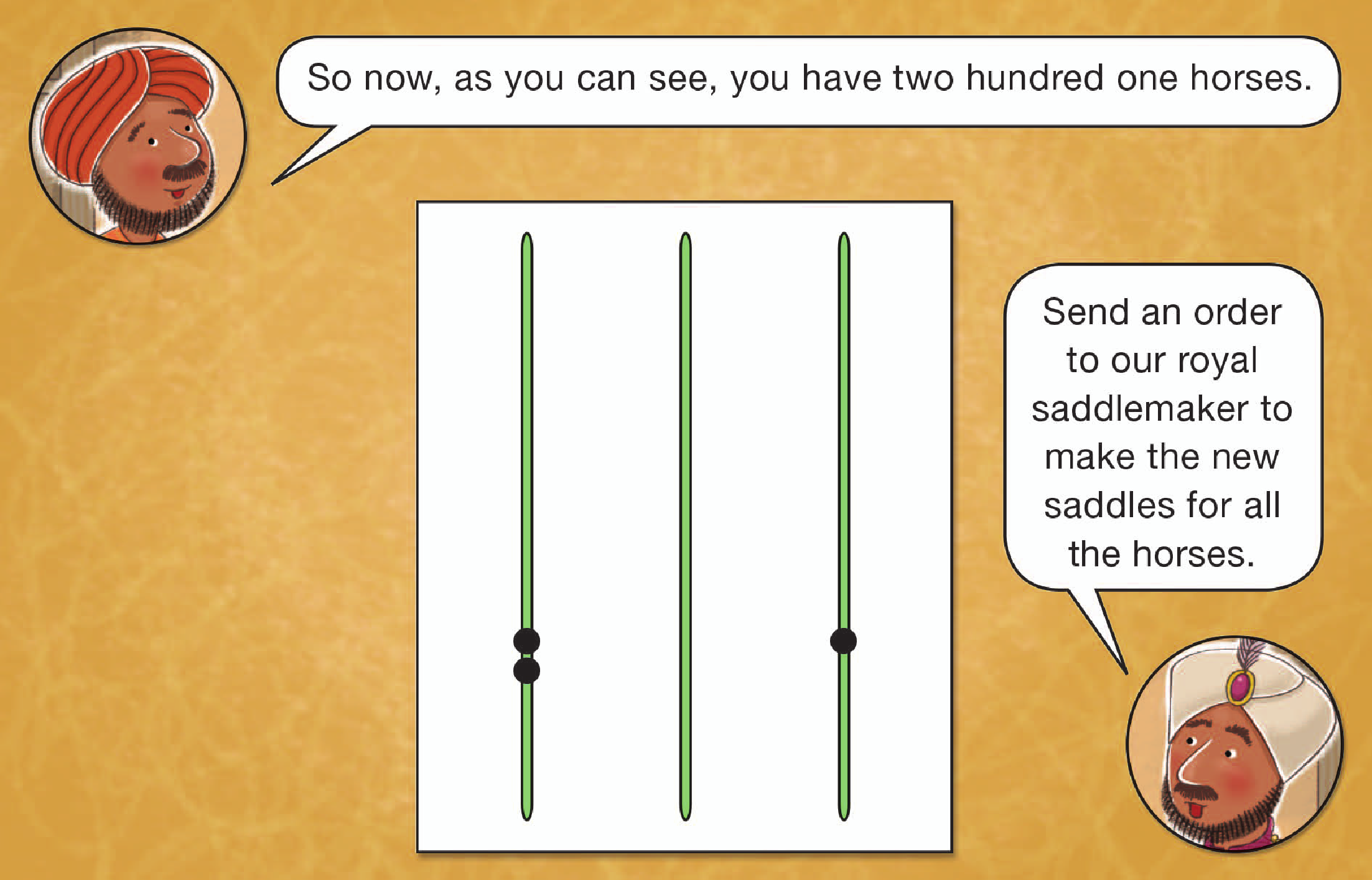
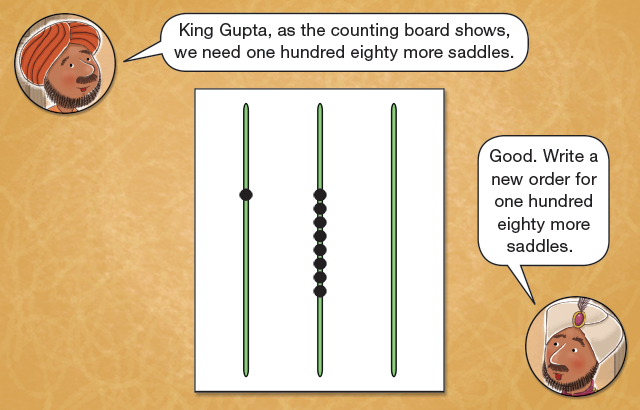
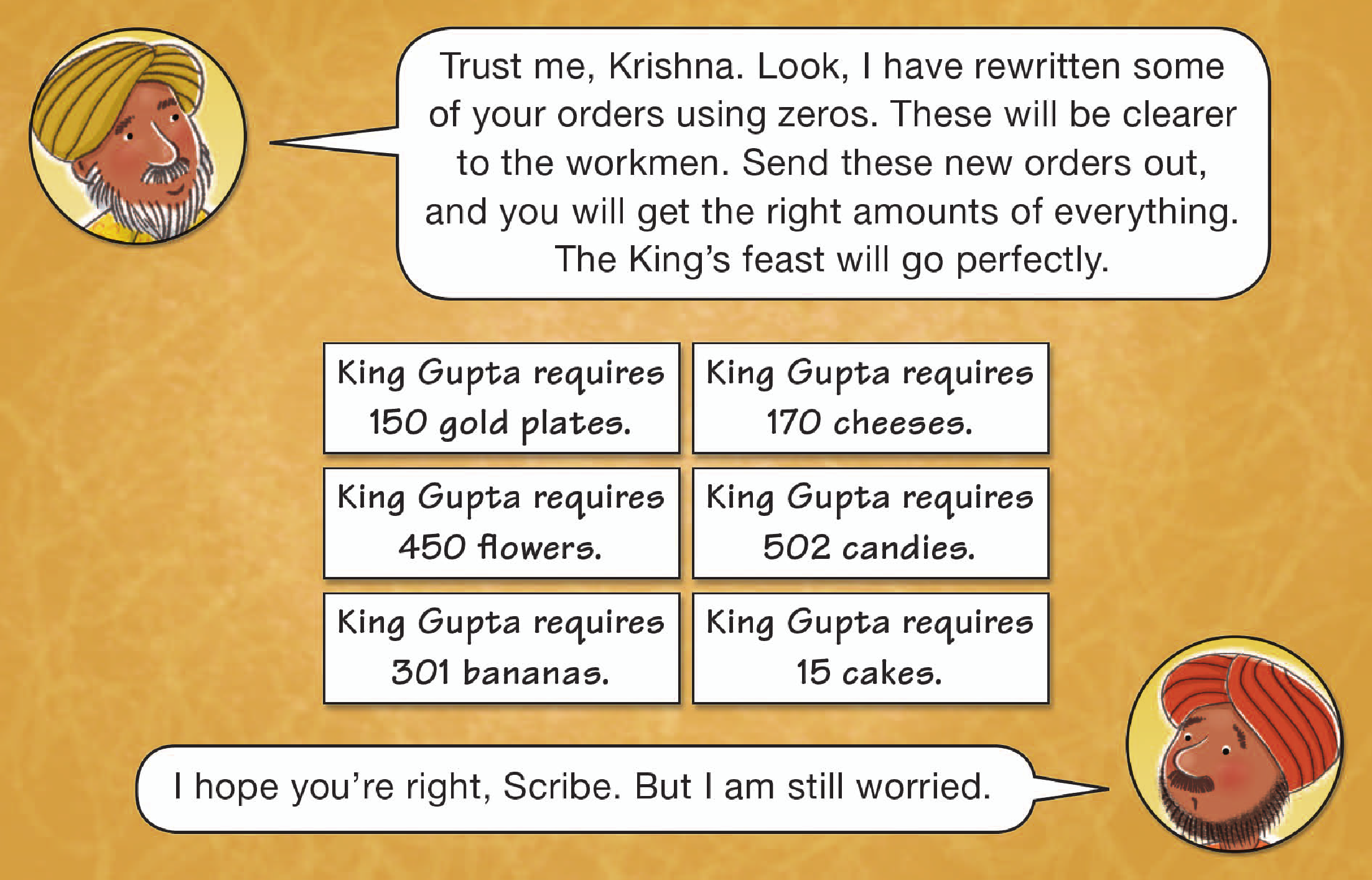
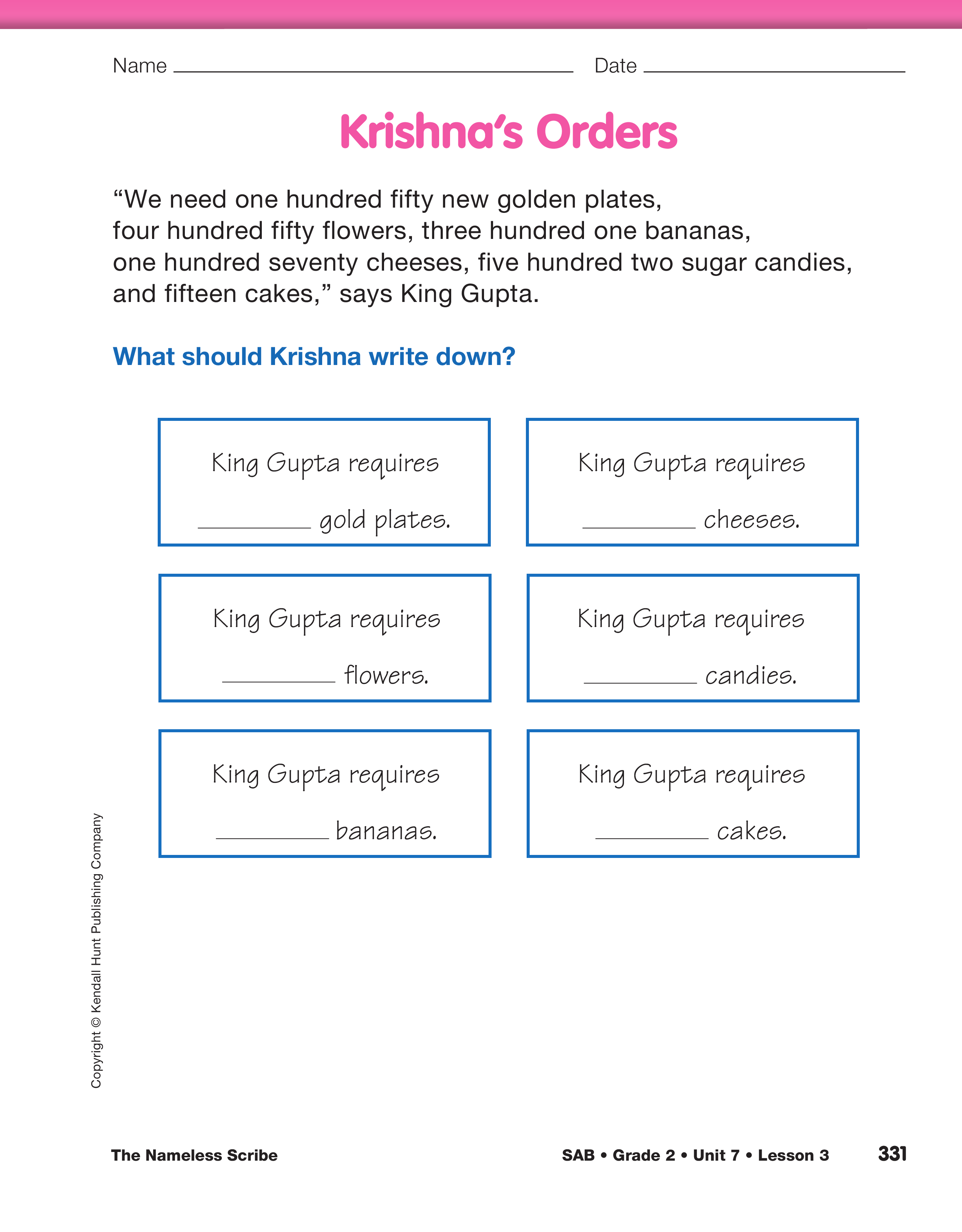
Direct students to the Krishna’s Orders page in the Student Activity Book. Read the number of different items that the king tells Krishna to order for the feast aloud as students read along. Students will write the numbers on the order sheets.

After students have completed the page, return to the story. The scribe’s work is done at this point in the lesson.

Page 20

Ask:

Compare your work to Krishna’s. Did Krishna write the numbers the same way you did? What’s different? What is the same? (Possible response: Krishna did not use zeros, he just left a space where a zero should be. I used zeros and have a digit in each place. We both wrote 15 for the cakes.)

Page 22

Ask:

If you could give Krishna one piece of wise advice, what would it be? (Possible response: Each place in a number needs a digit. You need zeros to hold the place in a number when there are no pebbles in a column on your counting board.)

Page 23–24

Ask:

How could Krishna make his orders for gold plates and bananas clearer? (He could write 150 gold plates and 301 bananas.)

Page 27–28

Words for Zero. Our word cipher comes from the Arabic word sifr, meaning empty (as in an empty column on a counting board or abacus). Zero comes from the same root. These and other mathematical terms deriving from the Arabic (e.g., algebra, algorithm) reflect the debt modern mathematics owes to medieval Islamic mathematicians.

Page 29

Ask:

What do you predict will happen when the workmen see the orders the scribe has written? (Possible response: They may still be confused because they don’t know what a zero is.)

The True Story of Zero. Several thousand years ago, the ancient Mesopotamians had a zero in their base-sixty place value number system. This number system was forgotten, however, when cuneiform writing fell into disuse about 200 bce, although remnants are preserved to this day in our measurement of time and angles. Some centuries later, about 600 ad, zero reappeared in northern India, either as a new invention or having been transmitted from the Mesopotamians. The details of this reemergence are sketchy, but it probably resulted from difficulties in recording numbers using only nine digits, as in the story of Krishna and Gupta. Over the succeeding centuries, the Indian method of writing numbers was transmitted to the Arabs in the Middle East and North Africa. During this period, the Arabs had the most advanced mathematics in the world. Beginning in the twelfth century, the so-called Hindu-Arabic system of numeration spread into Europe and eventually across the world.

Other cultures, notably the Maya in Central America, had number systems with symbols for zero. The zero that is used worldwide today descends from obscure origins in northern India more than 1000 years ago.

Page 35

Ask:

How do you think Heather’s mother feels about the question about silent e? (Possible response: She may have to make up another story about its invention.)
Why is the story called “The Nameless Scribe”?
(We never find out the scribe’s name.)

In this case, nameless does not mean that the scribe had no name, but that we do not know his name.