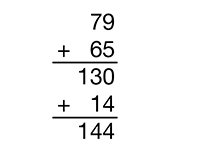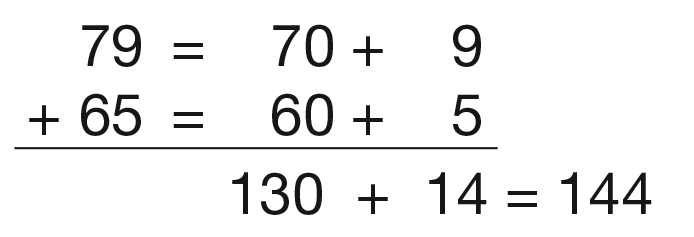Snack Shop Addition

Est. Class Sessions: 2

Developing the Lesson

Review Addition Strategies. Display the Addition Strategies Menu from the Student Activity Book Reference section. Write the following three problems on the board:

25¢	29¢	85¢
+ 25¢	+ 56¢	+ 30¢

Ask:

Which of the problems might you do in your head? with base-ten pieces? using the 200 Chart? using a number line? with paper and pencil?

Have students explain their thinking and demonstrate how they would solve one of the problems a particular way. Students may respond that they can solve 25¢ + 25¢ in their heads because they think about quarters. Some may prefer to use base-ten pieces or paper-and-pencil strategies to solve 29¢ + 56¢.
For 85¢ + 30¢, a student could start at 85 on the 200 Chart, and count three rows to add 30. Or start at 85 and take three hops of ten on the number line.

Estimate and Solve Addition Problems. Display the Shooting Star Snack Shop Children’s Menu page from the Student Activity Book.

Ask:

Look at the prices on the menu. If you had $2.00, would you be able to buy a pizza slice and a fruit salad cup? Explain how you know. (Possible response: I use friendly numbers. 79¢ is nearly 80¢ and 65¢ is in between two tens, 60 and 70. I would choose 70 so I made sure I had enough money. 80¢ + 70¢ is 150¢ so $2.00 is enough.)
Did anyone use a different estimation strategy or tool? Show us. (Possible response: I just looked at the tens. 7 tens plus 6 tens is 13 tens and that is 130. 130¢ is much less than $2.00 so the $2.00 would cover the items.)

Tell students to estimate, rather than find the exact sum. Students can use many techniques to estimate that they have enough money to buy the two items. Encourage students to share their estimation strategies. Try to select a variety of estimation strategies.

Next, ask students to find the total cost of 79¢ + 65¢ using any strategy. As they work, circulate and look at students’ solution strategies so you can select a variety to share.

Ask:

How did you find the sum of 79¢ + 65¢? (Possible response: I used all-partials. See Figure 1.)
Think about the estimates. Is your sum reasonable? How do you know? (Yes, the sum is reasonable because it is close to the estimate.)
Did anyone find the sum a different way? Explain. (Possible response: I used expanded form.
See Figure 2. )

Direct students to the Snack Shop Bills pages in the Student Activity Book. In Questions 1–3, students will look at the orders on the bills. They will first estimate the total cost and then find exact sums using both mental math and paper-and-pencil methods. Encourage them to refer to the Addition Strategies Menu in the Student Activity Book Reference section or to use their version from Lesson 6. Remind students to deter- mine if each answer is reasonable before going to the next bill. The prompt, “Is your total reasonable?” appears on each bill.

Use the Shooting Star Snack Shop Children’s Menu. Assign Questions 4–6. Students will fill in the remaining bills. These bills provide a limit as to how much money to spend. Students will choose 2–3 items from the menu and fill in the items on the bill along with the price. Before calculating, students should give an estimate that will help them determine if they have enough money. Finally, students will find the total cost and then determine if it is reasonable.

Students may work in pairs. One student may choose what he or she would like to order and estimate the cost. The other student can record the lunch order and then figure out the total cost. They can discuss the reasonableness of the total together.

Discuss Tools and Solution Strategies. Upon completion, provide an opportunity for students to share their solution methods. Talk about both estimation and addition strategies. Try to choose volunteers who can share a variety of strategies including all-partials, expanded form, and some mental math strategies.

Questions to ask include:

How did your estimate help you know if you had enough money to buy the items you listed? (Possible response: I estimated the cost of my items by adding the tens. I realized I had spent too much money so I chose a less expensive item.)
Show how you estimated the total cost.
How did you find the sum?
Is there another tool that could help you check the answer? (calculator)

Distribute the calculators and review the keystrokes for addition if necessary. Have students use their calculators to check their classmates’ answers. See Content Note.

Dollars and Cents. The concept of place value explains why 150 is greater than 105. There are five tens in 150 whereas 105 has zero tens. When writing 150 cents with a dollar sign and a decimal point, we write $1.50—the 0 here, as in 150 cents, is a place holder showing that there are no ones. In $1.50, the zero indicates there are no pennies. Notice what happens after you press the addition sign on your calculators in the following problem: 1.50 + 1.78. The zero in $1.50 is often deleted. The same problem in cents, 150 + 178, always looks the way you would expect on the calculator. The calculator cannot delete the zero in 150 because the value of the number would change to 15. The problem 60¢ + 84¢, in dollars and cents, is $0.60 + $0.84, Here the zero before the decimal point indicates that there are zero dollars. If you do not enter the first zero in $0.60 and $0.84 many calculators will do so for you. Thus if you enter .60 or if the answer is .60, it will appear as 0.6 on a calculator. This is likely to confuse students. You may prefer to have students enter the problem in cents, 60 + 84, and later convert the answer of 144¢ to $1.44.

ADVENTURE BOOK: