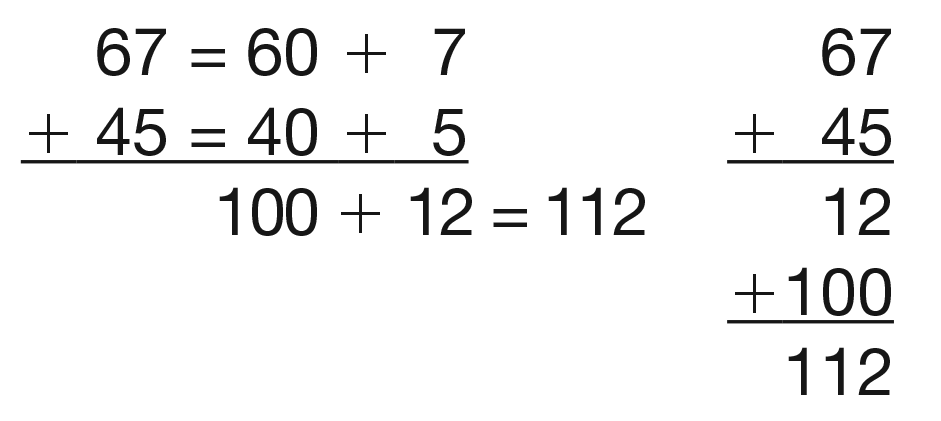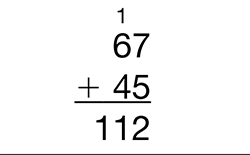Introduce the Compact Method. When students have finished
Questions 1–4, direct their attention to the
Compact Method section on the second page of the Help Them
Finish pages. See Content Note. Tell them that Julia solved 89 + 38 this
way. Give them some time to study her work with a partner, using
base-ten pieces to model and solve the problem. See Figure 5.

Challenges of Compact Method. The compact method is seen
as an efficient method, but it also comes with certain challenges. It
requires students to make trades in the middle of the process as opposed
to waiting until the end. The notation is not clear which makes it
difficult to look back and see what a student is thinking. The compact
method does not mimic how students use quantitative representations such
as connecting cubes or base-ten pieces. Other strategies are more
conceptual and more transparent. They make it easier to see a
student´s thought process and where they are making mistakes. That
said, many students already bring knowledge of the compact method to
school, so it is introduced in this lesson as yet another addition
strategy rather than the most effecient and best strategy.
Then have student pairs complete Questions
5–6. Encourage them to estimate the sums in the problems first and
to use base-ten pieces to model the problems.
Upon completion, discuss the problem in Question
5.
- When you solved 89 + 38 with base-ten pieces, did you make any trades? (Yes, I had 17 bits so I traded 10 of them for 1 skinny and I had 7 bits left over. I also traded 10 of my skinnies for 1 flat, and then I just had 2 skinnies left over. )
- If you leave it at 17 bits, does that follow the Fewest Pieces Rule? (No. You have to make it 10 + 7 and then trade the ten bits for one skinny.)
- If you trade the ten bits for 1 skinny in your head, how many bits will you have left? (7 bits)
- How did Julia show that she could make a ten with 9 and 8? (She put a little 1 above the tens column.)
- Why do you think she did this? (The little 1 helps her remember that the 9 and 8 make another ten.)
- What do you think the 7 in the answer stands for? (the 7 leftover bits or the 7 ones)
- When Julia added the skinnies, the tens, how many did she have? (Julia added 8 tens plus 3 tens plus 1 ten. 12 tens)
- How does she show that in her answer? (She wrote a 12 before the 7 ones.)
- Is there another name for 12 tens? (120)
- Putting that together with the bits or the ones, what is the sum? (127)
- Read the sum aloud. How many hundreds are in the sum? (1) Tens? (2) Ones? (7)
- How do you write that as a number sentence?
(100 + 20 + 7 = 127)
- What does that look like with base-ten pieces?
(1 flat, 2 skinnies, and 7 bits)
- Have all the trades been made so that there are the fewest pieces? (yes)
Tell students that Julia used a paper-and-pencil method to
add that helped her make trades in her head called the compact
method. She used the Fewest Pieces Rule. The little 1 in the tens
column reminded her that she needed to add another skinny, a ten,
to the tens that she already had. The little 1 always means you
are adding one ten to the tens column. This method takes less
writing than the other two paper-and-pencil methods, expanded
form and all-partials, because some of the trading steps are kept
"in your head" and not written down.
Ask student volunteers to model the problems in Question 6
with base-ten pieces and then others to demonstrate how they
solved the problems using Julia´s compact method. As you discuss
the method, ask students to connect the numbers in the ones place
to the bits and the numbers in the tens place to the skinnies.
When students explain how they traded bits (ones) for a skinny
(ten), then added it to the number of skinnies in the tens place,
question them to be sure that they know they are adding tens.
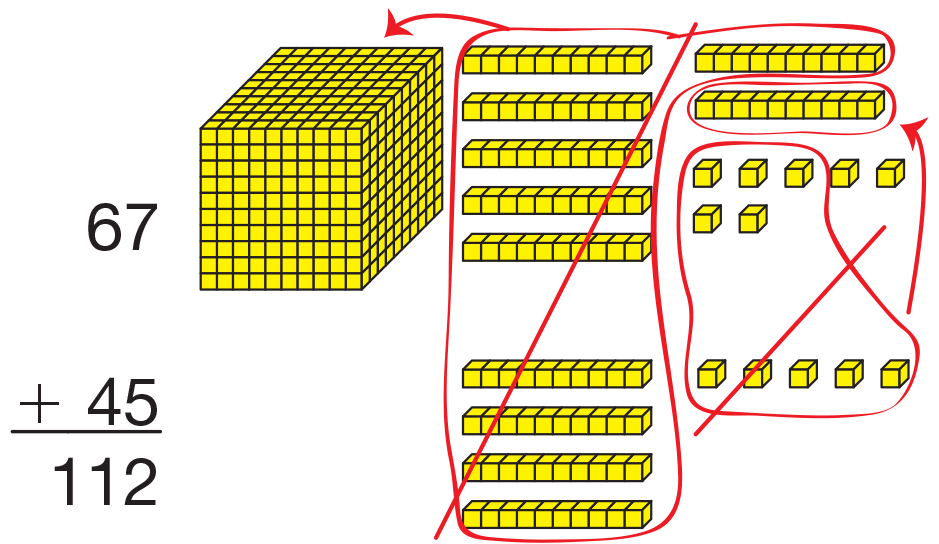
Trade Skinnies for Flats. Display 67 + 45. Display the
base-ten pieces for the problem and ask students to estimate the
sum. Then ask them to use their pieces to total the number of
skinnies and bits. Ask students to make all trades as necessary
for the Fewest Pieces Rule. See Figure 6.
As a student uses display pieces to demonstrate the trades, ask:
- What trades did you make? (I traded 10 bits for a skinny and 10 skinnies for a flat.)
Tell students to solve the problem using both the expanded
form method and the all-partials method. Make connections between
the steps of each method and the base-ten pieces. Ask questions
about what happens when the tens are added in this problem using
either of these two methods. See Figure 7.
- What do you get when you add 6 skinnies and 4 skinnies? (10 skinnies)
- Can you say that using tens? (6 tens plus 4 tens is 10 tens.)
- Is there another way to say and write 10 tens? (100)
- When you added the ones, did you have enough to make another ten? (Yes, 7 plus 5 will make another ten with 2 left over.)
- How much is 10 tens plus 1 ten plus 2 ones? (Possible responses: 11 tens plus 2; 110 + 2; 112)
Now ask students to solve the same problem using the
compact method as in Figure 8. Have a student volunteer
demonstrate the method.
Ask questions about all the steps taken:
- Why did you just write a 2 under the line in the first column? (I added the 7 and 5 and got 12. I can´t put 12 in the ones column. It´s really ten ones and 2 ones. I just wrote the 2 ones down.)
- What will you do with the ten ones? (I have to trade the ten ones for a ten so I put this little "1" in the tens column.)
- Why did you do that? (I have to remind myself to add another ten.)
- How many tens do you have now? (I had 6 tens and 4 tens. That´s 10 tens. Then another ten that I got when I traded. That makes 11 tens.)
- How much is 11 tens? (110)
- How do you know? (Possible response: I know 10 tens is 100 so 11 tens is 100 + 10, 110.)
- What is that with base-ten pieces? (11 skinnies.)
- So, how many hundreds, tens, and ones do you have? (1 hundred, 1 ten, and 2 ones)
- What number is that? (112)
- What does the 1 in hundreds column stand for? (100)
- What does the 1 in the tens column stand for? (1)
- Why is the value of the 1 different? (Its value depends on where it´s placed within the number, the hundreds place or the tens place.)
Discuss with students the question of whether they start a
problem by adding the ones or the tens. Ask the class to solve 58
+ 67. Ask half of the class to solve it using all-partials
and half using the compact method. See Sample Dialog and
Content Note.
Starting on the Right or the Left. For both the expanded
form and the all-partials methods of addition, it doesn´t matter
whether a student starts on the left or the right. In either
method, a student may choose to add the tens before the ones or
vice versa with no loss of efficiency or accuracy. When using
the compact method, however, it will be helpful if students are
guided to start on the right; that is, to add the ones before
adding the tens. Students may be inclined to start on the left,
since they are learning to read from left to right. Starting on
the left when using the compact addition method is possible, but
it usually entails additional steps and can be confusing and
lead to mistakes.

Teacher: Luis, show us how you used all-partials. When you were solving this problem, which did you add first: your ones or your tens?
Luis: I started with my tens.
Teacher: How did that work?
Luis: Well, it was okay. I got 125.
Teacher: Did anyone start with the tens using the compact method? John, you did? What happened when you added the tens first when you did it this way? Show us.
John: I added 5 + 6 and I got 11 tens. 11 tens is 110. That is 1 hundred and 1 ten. So I wrote a 1 in the hundreds column and another 1 in the tens column.
Teacher: Okay. Now what about adding your numbers in the ones column? What did you get?
John: I got 15.
Teacher: What does that 15 mean?
John: It means 15 bits, which is 10 and 5 bits. I wrote the 5 in the ones column.
Teacher: What did you do with the ten?
John: I put it in the tens column, but I had already added that column. So I had to go back to the tens column again and change it. I got 125 too, but I had to cross out.
Teacher: What did you decide about starting on the left?
John: I got the same answer as the other way but I had to cross out. I decided it´s more efficient to start on the right and add the ones first when I do the compact method.
Practice Paper-and-Pencil Methods. Assign the Use
Paper and Pencil pages in the Student Activity Book to
provide practice with three paper-and-pencil methods of addition;
expanded form, all-partials, and the compact method. The
assignment includes problems in which two trades have to be made.
Remind students to estimate the sums first to determine whether
their answers are reasonable.
Upon completion, choose one problem to solve using all
three paper-and-pencil methods. Have a student model the problem
with base-ten pieces and others display the steps they took with
expanded form, all partials, and the compact method.
- Did all the methods help you find the same sum?
- Did one use less writing than another?
- Which method do you find easiest to understand?
- Which way or ways help you avoid making mistakes?
- Which method do you like best?