Development of Addition Methods

In this unit, students develop meaningful, accurate, and efficient methods for two-digit and three-digit addition. The development of computation methods in Math Trailblazers is based on research that corroborates the relationship between conceptual understanding and procedural fluency (Fuson & Burghardt, 2003; Fuson, 2003; Verschaffel, et. al, 2007; National Research Council, 2001; NCTM, 2000; Hiebert & Wearne, 1996).

Throughout the curriculum, students are encouraged to create their own ways to add. This approach is based on research that shows that understanding number and operation concepts greatly increases students' success with algorithms (Coburn, 1989; Hiebert, 1999; NRC, 2001). Several approaches to teaching paper-and-pencil addition can be identified that include letting students devise their own procedures. Madell (1985), Swart (1985), and Kamii (Kamii, et al., 1993) all endorse this approach, especially for initial instruction.

There are, however, good reasons for teaching algorithms that Fuson (1987), Schoenfeld (1994), Usiskin (1993), Carpenter, et al. (1992), and Bass (2003) endorse. First, teaching algorithms reinforces place value concepts and provides increased understanding of numeration. Second, there are times when it is just as easy to use paper and pencil as it is a calculator. Third, you may need to check a restaurant bill or other calculation when a calculator is not available. And last, but not least, the idea of an algorithm is an important one. The power of mathematics comes in part from algorithms. Algorithms, because of their repetitive nature, allow us to complete routine problems with ease.

Using the research cited above, students first invent strategies to solve problems in an Addition Seminar and then develop their own methods to solve addition problems using base-ten pieces. Base-ten pieces are effective if students are given enough time to think for themselves how to compose and decompose numbers in order to combine quantities. Then, students need to connect their experience with the base-ten pieces to written symbols (NRC, 2001, p. 198; Fuson and Burghardt, 2003, 289–290).

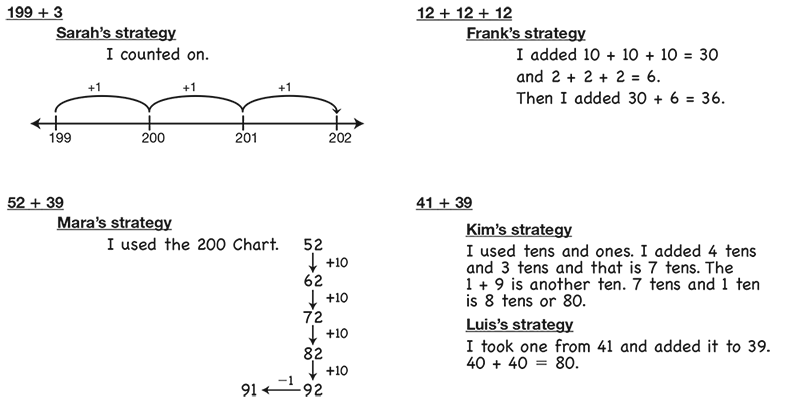
Figure 1: A chart of Invented Strategies from Lesson 2

Throughout the unit, students share their own strategies with their classmates and read about possible strategies in the Student Activity Book. See Figure 1. Comparing the various strategies and trying them out allows students to analyze the efficiency and usefulness of the methods in different situations and improves students' understanding of place value representations (NCTM, 2000, p. 153; NRC, 2001, p. 196).

Two of the methods illustrated in Figure 1 are mental strategies. Each is useful in different situations:

• Finding Friendly Numbers. Students learn to use friendly numbers to mentally estimate to see if their answers are reasonable.
• Counting On. Students can often add two-digit numbers mentally using counting strategies, especially when the numbers are close to multiples of ten. The 200 Chart and number line can help support these counting strategies. Encourage students to use these tools to support and describe their thinking. With time, these tools will become mental images that support student thinking.

Three of the methods are paper-and-pencil methods. Each has advantages and disadvantages for students:

• Using Expanded Form. We introduce this method to reinforce the place value concepts that underlie addition. Since students must write a number sentence to show the tens and ones, they are reminded that when they add 64 and 28 they must add 6 tens and 2 tens or 60 and 20, not 6 and 2. This helps combat misconceptions that numbers in an addition problem are just single digits lined up in columns.
• All-Partials Method. This method is called the all-partials method because the partial sums are recorded. It is transparent in that it is very easily understood and explained by students. Like using expanded form, it helps students understand what they are actually adding—tens and ones as opposed to single digits. All trades are made in the final steps of the process. This can improve accuracy for students who have trouble keeping track of their trades.
• Compact Method. This method is the algorithm that is traditionally taught in the United States. Trades are made mentally and tracked in the middle of the process. Using both the methods described above can help students better understand this algorithm. Students will understand the regrouping process better if they understand the place value concepts underlying the procedure. Otherwise, they are more likely to make systematic errors based on their misunderstandings and notation errors (NRC, 2001, p. 196). We found from our research that students sometimes make the errors shown in Figure 2.

Figure 2: Possible addition errors

In A, students added the individual digits of the two addends, instead of considering the value of each place. In B, students did not make any trades and just wrote down the sum of each column. In each case, asking students to first consider whether the answers are reasonable will often alert them to the fact that they have made an error. Then, asking them to think about the value of the digits and to link their written method with baseten pieces will often help students correct their own errors (Fuson and Burghardt, 2003, p. 289).

Choosing Appropriate Strategies

Students who are proficient with addition are able to choose strategies that are appropriate to the situation and efficient. For a strategy to be efficient, it is not only characterized by the fewest and quickest steps. To be efficient, a strategy must also consistently yield an accurate response, be easy to understand, and fit the problem. For example, to solve 699 + 789 a student could choose the compact method because there appear to be fewer steps, when in fact, a mental math strategy is probably more efficient.

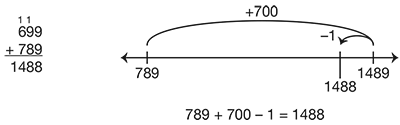
To help students develop this flexibility and to give them experience with making critical choices, many of the addition strategies and methods are organized into a menu. This menu summarizes the strategies and methods introduced in the unit as well as those students invent. In Lesson 6, students are given the opportunity to add their own invented strategies and methods to the menu.

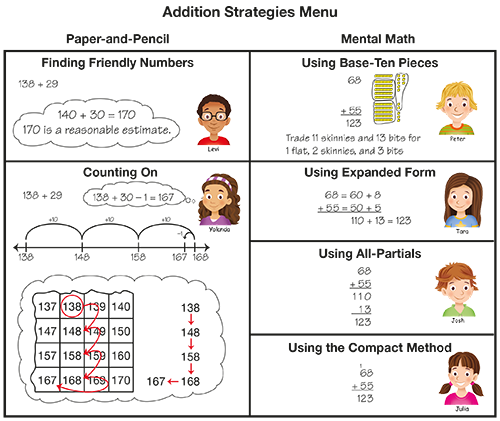
Figure 3: Addition Strategies Menu

Students will gravitate to strategies and methods that make sense to them. Students do not need to be experts at all the strategies and methods, but rather should find a few strategies that work for them. In time, they will expand their cadre of strategies.

Estimation

Estimation is found throughout the Math Trailblazers™ curriculum. In this unit, we discuss one tool that is frequently used when estimating the result of a computation—finding a "friendly" number that is close to a given number. For example, find the sum of 57 and 74 by thinking that 57 is close to 60 and 74 is close to 75, so the sum is close to 60 + 75. Students first work with base-ten pieces to develop their sense of numbers in relation to "friendly" numbers like multiples of 10 or 100. Another tool for estimating sums is the use of an interval or range in which the result can be found. Using the previous example, students would note the intervals in which 57 and 74 could be found (either on their 200 Charts or number lines). The sum of 57 and 74 lies between 120 (50 + 70) and 140 (60 + 80). Estimation is discussed as a way of finding reasonable, close answers and a way of predicting or checking answers. We introduce these ideas before students work on paper-and-pencil methods for exact answers, so that they are encouraged to use mental strategies for estimates.

Practice

Practice is an essential part of mathematics. Fluency with basic procedures enhances conceptual understanding of new material. It is achieved gradually over time and is maintained with regular and consistent practice. In Math Trailblazers ® the practice of addition and subtraction is implemented according to the following three considerations:

1. Practice is distributed over the curriculum. Students do short sets of problems frequently, rather than many problems all at one time, especially in the Daily Practice and Problems and Home Practice.
2. Practice is embedded in problem solving in the lessons, activities, laboratory investigations, and games.
3. Students practice material already mastered while learning new content.

This program of practice allows teachers to monitor students' addition strategies as they develop. Teachers can quickly identify incorrect procedures and help students correct them before they become ingrained.