Workshop: Addition Strategies

Est. Class Sessions: 2–3

Developing the Lesson

Part 1: Addition Strategies Practice

Explore a Variety of Strategies. Display the problem 39 + 11 and ask students to first estimate the sum. Review that estimation is a way of finding reasonable, close answers and a way of predicting or checking answers to computation problems. Students may round using benchmarks, use friendly numbers, compose and decompose numbers, or count on.

Then ask students to solve the problem. Encourage them to use number lines, base-ten pieces, or the 200 Chart.

Ask:

Compare your estimate to your answer. Does your answer seem reasonable?
Did anyone use paper and pencil to solve this problem?
Did anyone use mental math?

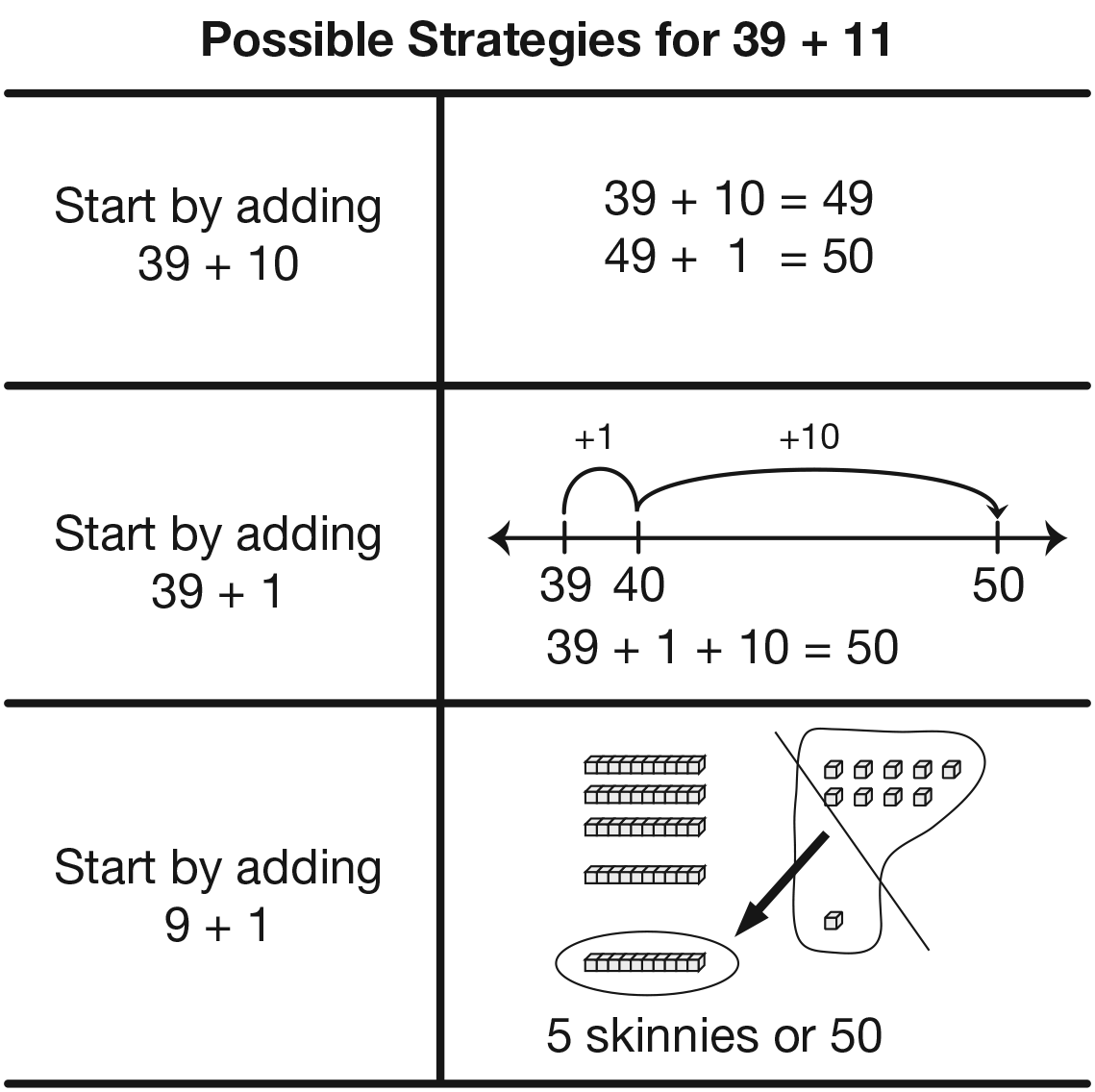
Remind students that there are ways other than using paper and pencil to add. The compact method is not the end point for all problems. While it is certainly a useful and important strategy, it is not the only way to solve a problem. Sometimes a paper-and-pencil method is not the quickest or most efficient way to solve a problem. To emphasize this point, ask the students to solve this same problem by starting several different ways:

Start by adding 39 + 10.
Start by adding 39 + 1.
Start by adding 9 + 1.

Have students share how they finished each of these strategies. See Figure 1 for possible solutions. Even after students have developed proficiency with paper-and-pencil algorithms, these other methods are helpful for mental arithmetic and estimation.

Discuss Efficiency of Strategies. At this point, students do not have enough experience to choose the most efficient strategy for a given problem. However, it is important for them to begin comparing strategies. See Content Note and Sample Dialog.

Ask:

Did each way help us reach the correct answer?
Which way did you like best? Why?
Was there a way that was more difficult or confusing?
Is one way done with a lot of steps?
Can one of the ways be done in fewer steps?
Does one way help you solve the problem more quickly?
Which way is the most efficient or easiest to think about in your head? Why?

Students may not be motivated to seek a more efficient strategy at first because they are confident with a less efficient strategy. This exercise will start students thinking that some strategies are better than others for some problems. Remind students that an efficient strategy:

reaches the correct answer
fits the problem
can be done in fewer steps
can be done quickly
is easy to understand

Building Capacity to Choose. As they build experience and confidence with the strategies, students will be better able to select more appropriate and efficient strategies. For now, getting students to explore the question of which strategy makes the most sense for a given problem is appropriate. They may not always agree on what is the most appropriate or efficient strategy. For example, for some students the compact method may be one where error is common. Therefore, the strategy is not efficient because students do not consistently get an accurate answer.

In this discussion, students compare strategies for solving 21 + 22 and then 38 + 13.

Teacher: Can someone show us how they solved 21 + 22?

Nila: Yes. I did 20 + 20 which is 40 and 1 + 2 which is 3. So the answer is 43.

Teacher: Can someone tell me what Nila did first?

Roberto: Nila added the skinnies first and then the bits.

Teacher: Can someone show us another way to solve this problem?

John: Yes. [John goes to the board and writes a solution to this problem using the compact method.] 21 + 22 = 43.

Teacher: What did John do first?

Linda: John could have added the skinnies or the bits first. He didn´t trade anything and it does not matter.

Teacher: Which strategy do you like best?

John: I like the compact method that I used because it is easy.

Nila: I liked adding the skinnies first because I could do the whole problem in my head.

Teacher: Can someone show us how they solved
38 + 13?

Jerome: Yes. I split 13 into 2 + 10 + 1 to add the 2 to 38. 38 + 2 = 40. 40 + 10 = 50 and 50 + 1 = 51.

Teacher: I think some of us had trouble following what you were doing. Can you show us what you did on the number line or some other way?

Jerome: [Jerome writes 38 + 13]. Now I am going to rewrite the problem to show how I split 13. [Jerome writes 38 + 2 + 10 + 1. Jerome then moves to the number line to show the moves on the number line.] 38 + 2 is 40 and then a hop of ten takes us to 50. 50 + 1 = 51.

Teacher: Is this answer reasonable and how do you know?

Ming: Yes. 38 is about 40 and 13 is about 10. So 40 + 10 is 50 which is close to Jerome´s answer.

Grace: I solved this problem using expanded form. 38 + 13 = 40 + 11, which equals 51.

Teacher: Which strategy do you like best for this problem?

Jerome: I like counting on. I can see it on the number line.

Grace: I like the expanded form because it is like the base-ten pieces without having to do all the trades.

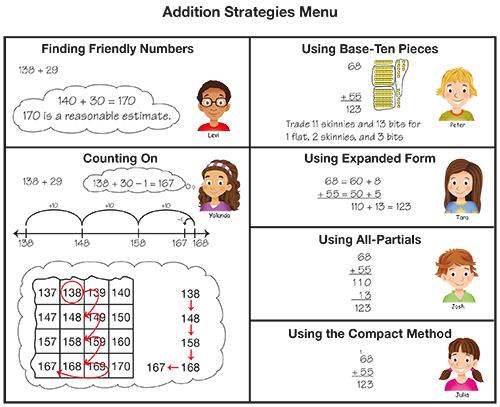
Review Addition Strategies Menu. Explain that this Workshop gives students the opportunity to practice many different addition strategies. Display Addition Strategies Menu from the Student Activity Book Reference section and ask students to look at their version from Lesson 6.

Ask:

Do you recognize all the strategies given?
Which is your favorite strategy to use? Why?
Do you know how to use all the strategies?
Could you use one strategy to solve every problem? (probably)
Do some strategies work better for some kinds of problems? (yes)
Would you choose a mental math strategy or a paper-and-pencil strategy to add 20 + 29? Which do you think would be most efficient? (Possible response: Mental math is an efficient way to add numbers that have ending zeroes like 20 or numbers that are close to numbers with ending zeros, like 29. I think 20 + 30 − 1 = 49.)
How about 34 + 78? Would you choose mental math or paper and pencil? Why? (Possible response: paper and pencil because there are no zeros and two trades; mental math because I know 70 + 30 is 100 and 8 + 4 is 12, so 34 + 78 = 112)

The Addition Strategies Menu is designed to help students choose different, appropriate, and efficient strategies. It also allows you to help students focus on certain strategies and not others, if you choose. For students struggling with addition, have them focus on the all-partials method or using expanded form. For students who are confident with addition, ask them to use a mental math strategy and focus on finding efficient strategies for each problem.

Tell students that as they become proficient with more strategies, they will have a greater collection with which to solve a variety of problems.

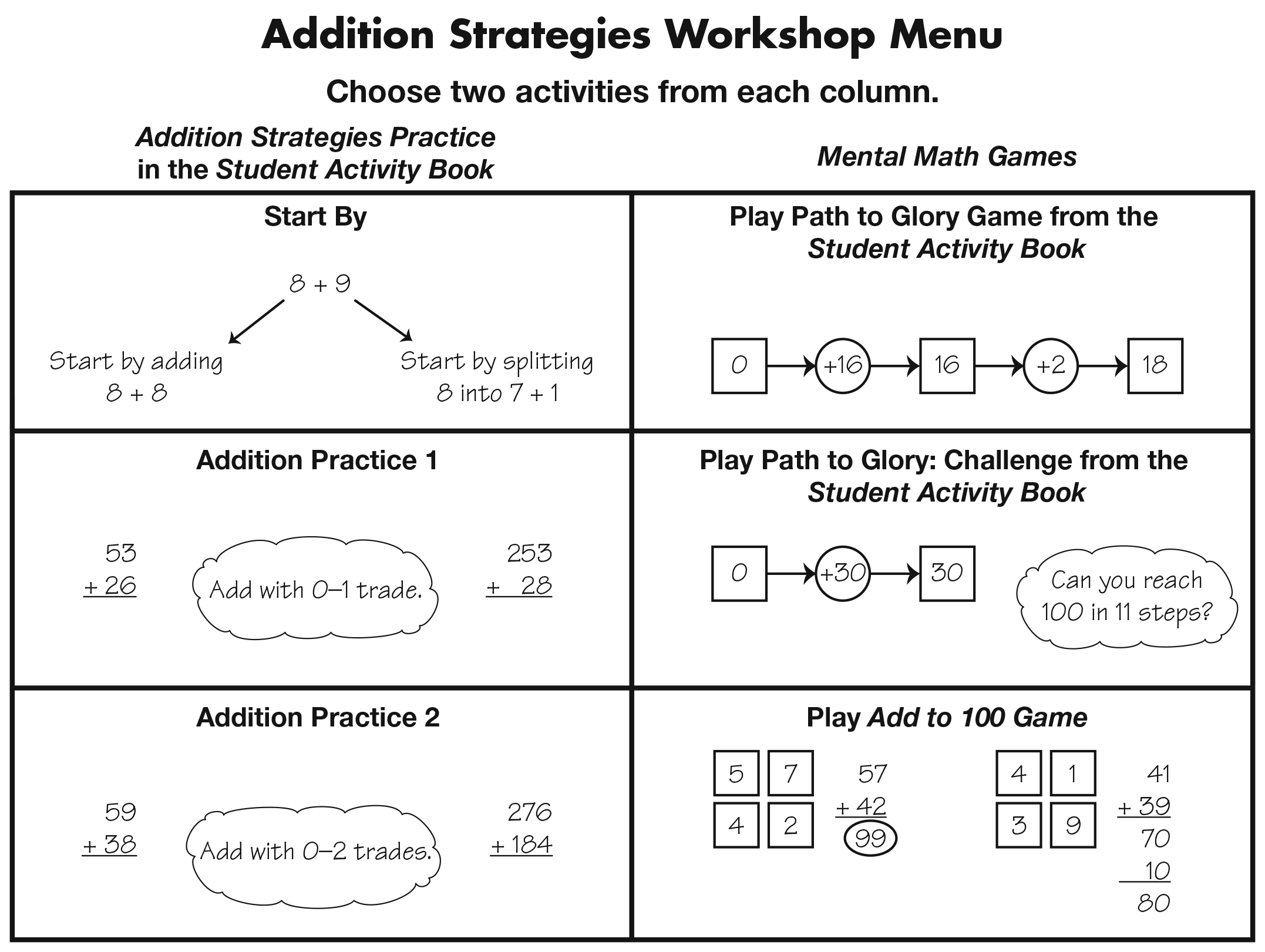
Introduce Addition Strategies Workshop Menu and Choices. Display the Addition Strategies Workshop Menu from the Student Activity Book. See Figure 3. Explain to students that they will use this menu to help them choose addition practice. The practice listed in the first column focuses on using addition strategies. The second column focuses on using mental math strategies. In the first part of the Workshop, students will consider the activities from the first column.

Provide an overview of students´ practice choices. All of the activities require students to solve the same problem two ways. This expands students´ proficiency with a variety of strategies and encourages them to consider the efficiency of strategies. It also encourages students to compare strategies, check for reasonableness, and check for and correct mistakes.

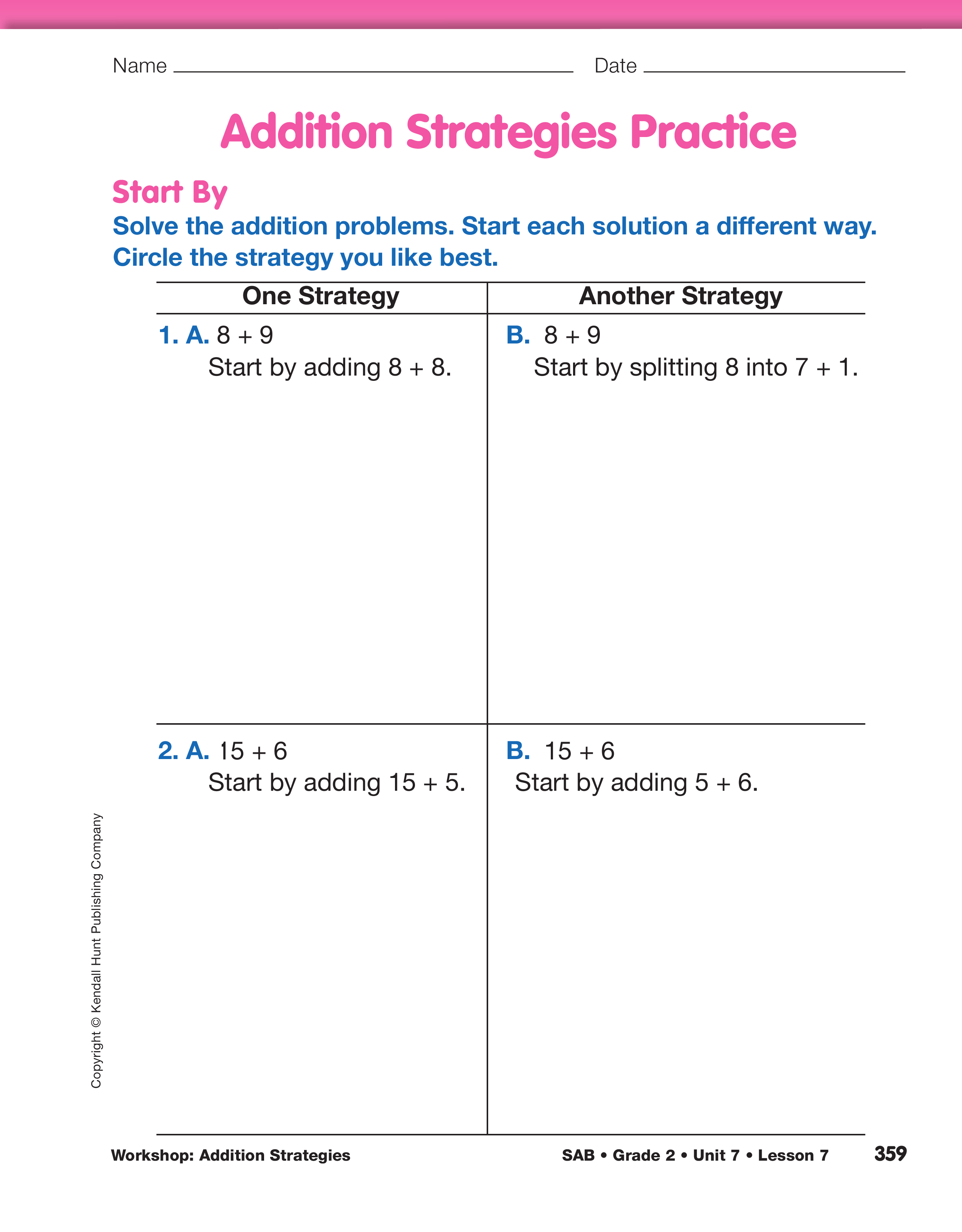
Direct students´ attention to the Start By section of the Addition Strategies Practice pages in the Student Activity Book. The problems on these pages are similar to the opening activity. If students choose this practice, they will solve each problem two ways. They will need to show how they finish each problem and circle the strategy they like better.

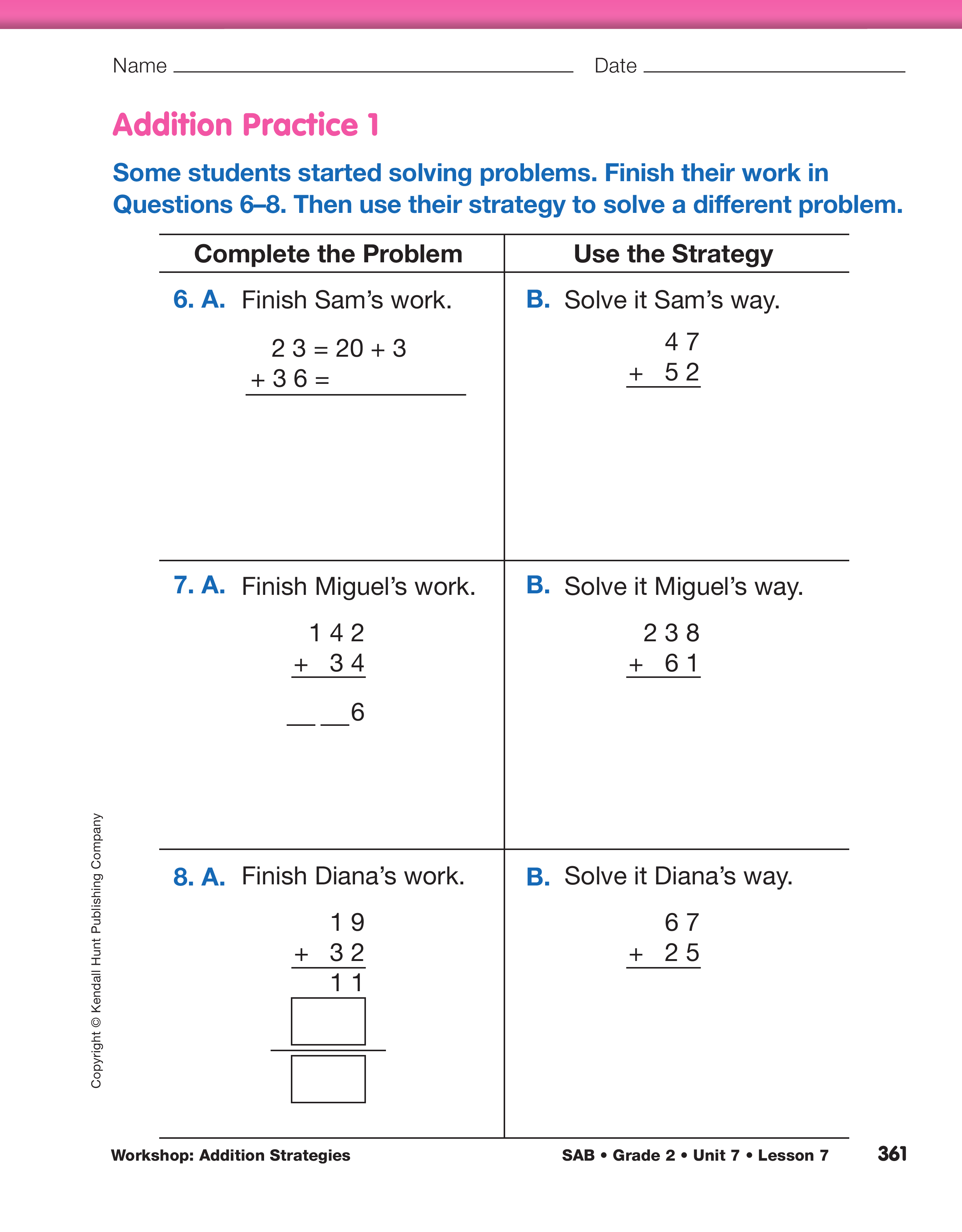
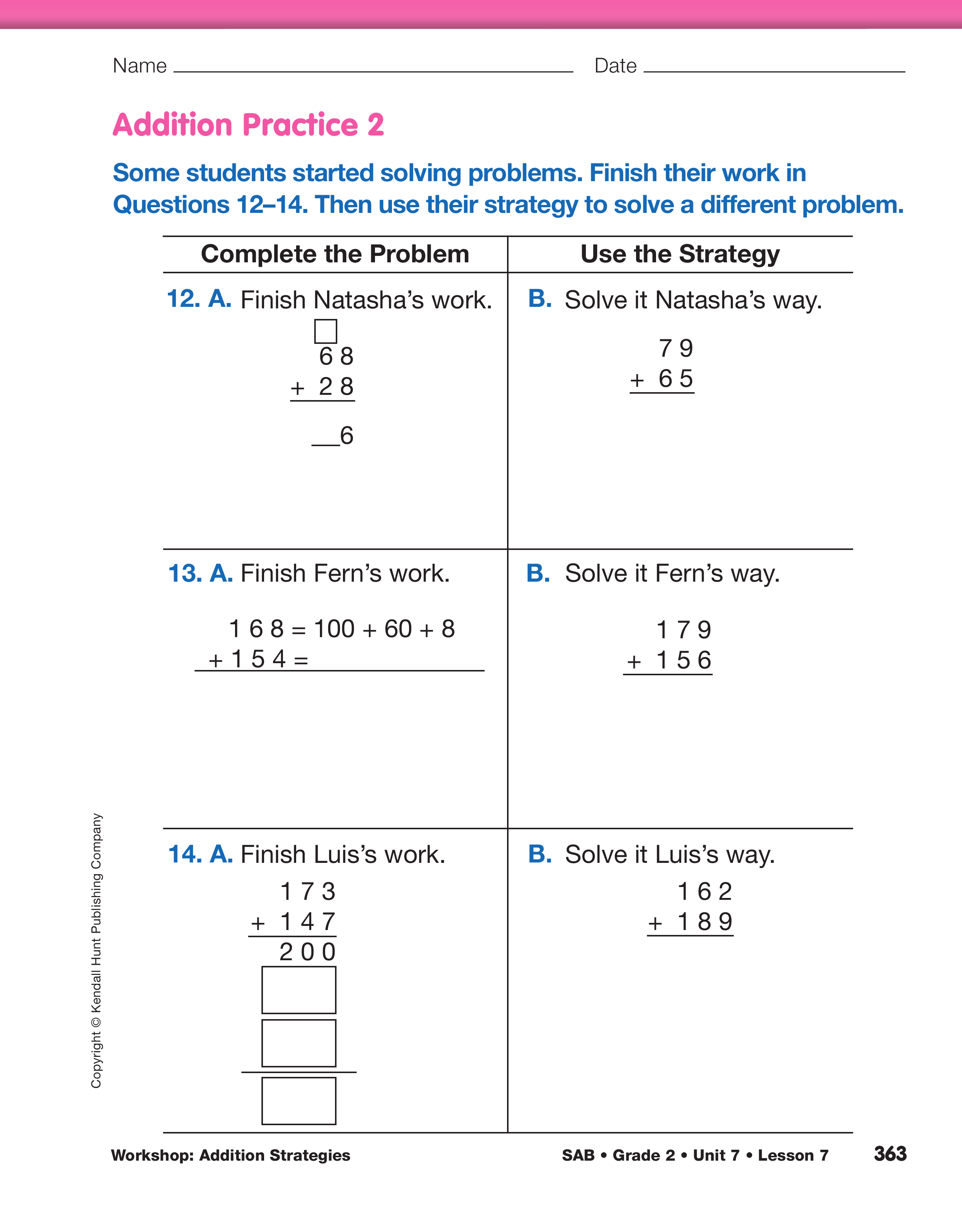
Students may choose to solve problems from the Addition Practice 1 or Addition Practice 2 sections of the Addition Strategies Practice pages. The problems in the Addition Practice 1 section provide practice with adding 2- and 3-digit numbers and making one or two trades. The Addition Practice 2 section involves adding 2- and 3-digit numbers with multiple trades and is more challenging. Suggest that students try to solve the sample problems given on the menu to help them determine their confidence levels with these skills when choosing between the two. Some students may choose to do both sections. (Minis not shown here are in the Answer Key.)