An Addition Seminar

Est. Class Sessions: 2–3

Developing the Lesson

Develop Invented Strategies for Addition. Begin the lesson by telling students that they are going to have a “strategy session” similar to the strategy session they had for addition facts with sums to 20 earlier in the school year. In this strategy session, they will solve addition problems with larger numbers and pay special attention to the strategies they use.

Introduce the problems on the Addition Strategy Session page in the Student Activity Book.

Say:

There are six problems at the top of the page. Look at each problem with your partner and discuss different ways to solve each problem.
Now that we are adding larger numbers, I want you to think of strategies that are more efficient than using counting on or counting all.
If you would like to use tools such as the number line, 200 Chart, base-ten pieces, or connecting cubes, explain how you would use those tools to solve the problem.

Have student pairs discuss strategies for solving each problem. Then have students select two of the problems and write their strategies for solving them. Explain to students that for each problem, they should show or explain how they solved the problem and not just name the tool they used. If students finish early, encourage them to think of more than one way to solve each problem.

After providing adequate time for students to work, select one problem at a time and ask student volunteers to demonstrate how they solved the problem. Have the prepared Number Line Display, a 200 Chart, base-ten pieces, and connecting cubes available for students to use as they describe their strategies.

Ask:

Who can explain your strategy for solving the problem 199 + 3? (Possible response: I counted on. I started at 199 and counted three more. The answer is 202.)
Did someone solve it another way?

After a student has explained a strategy, identify it by that student’s name and record the strategy on a piece of chart paper labeled, “Addition Strategies Chart.” See The Naming Stategies Content Note. As you continue discussing strategies for other problems, ask students to solve the problem using one of the named strategies on the chart. See Figure 1 for a sample chart of invented strategies.

Naming Strategies. There are many different ways to name a strategy. Encourage students to use names that are meaningful and will help them remember the strategy. Names can be related to the steps in the strategy, such as counting back or counting up. Names can also be selected because students associate the strategy with a particular student in the class who regularly uses it. It is not important that students be able to name the strategy, though it does help them discuss and distinguish between them.

Students may use the same basic strategies but call them by different names. For example, from a teacher's perspective, when a student uses a number line or a 200 Chart, he or she uses the counting-on strategy. Even though it is the same strategy, it is acceptable for students to name it separately.

Computation is an important topic in mathematics. Studying computation serves as a rich vehicle for building mathematical understandings (Hiebert, et al. 1997). Children can and do devise or invent algorithms for carrying out multidigit computations. "Opportunities to construct their own procedures provide students with opportunities to make connections. . . . The invention itself is a kind of problem solving, and they must use reasoning to justify their invented procedure. Students who have invented their own correct procedures also approach mathematics with confidence. . ." (National Research Council, 2001. See also Kamii and Dominick, 1998).

In this unit we are laying the groundwork for helping students grapple with why the addition algorithm works. We do so by asking students to invent their own strategies, estimate sums, determine if estimates are reasonable, and use base-ten pieces to concretely represent the need for trading (or regrouping). Research confirms that this is a valuable approach.

Hiebert, James, et al. Making Sense: Teaching and Learning Mathematics with Understanding. Heinemann Publishers, New Hampshire, 1977.

Kamii and Dominick. “The Harmful Effects of Algorithms in Grades 1–4.” In The Teaching and Learning of Algorithms in School Mathematics. Morrow and Kenney, eds. National Council of Teachers of Mathematics, Reston, VA, 1998.

National Research Council. “Developing Proficiency with Whole Numbers.” In Adding it Up: Helping Children Learn Mathematics. Kilpatrick, Swafford, and Findell, eds. p. 197. National Academy Press, Washington, DC, 2001.

After students demonstrate their strategies and record them on the chart, ask questions similar to the following:

Which strategies do you think are the easiest to use? Why?
Which strategies are the hardest to use? Why?
Could you use different strategies for different problems?
Is there a strategy you do not understand?
Which strategies are the most efficient?

Help students to understand that a strategy that is efficient for one problem can be inefficient for another. For example, using counting on by ones is an efficient strategy for 199 + 3, but it is not an efficient strategy for 51 + 24.

Leave the Addition Strategies Chart on display throughout the rest of the unit.

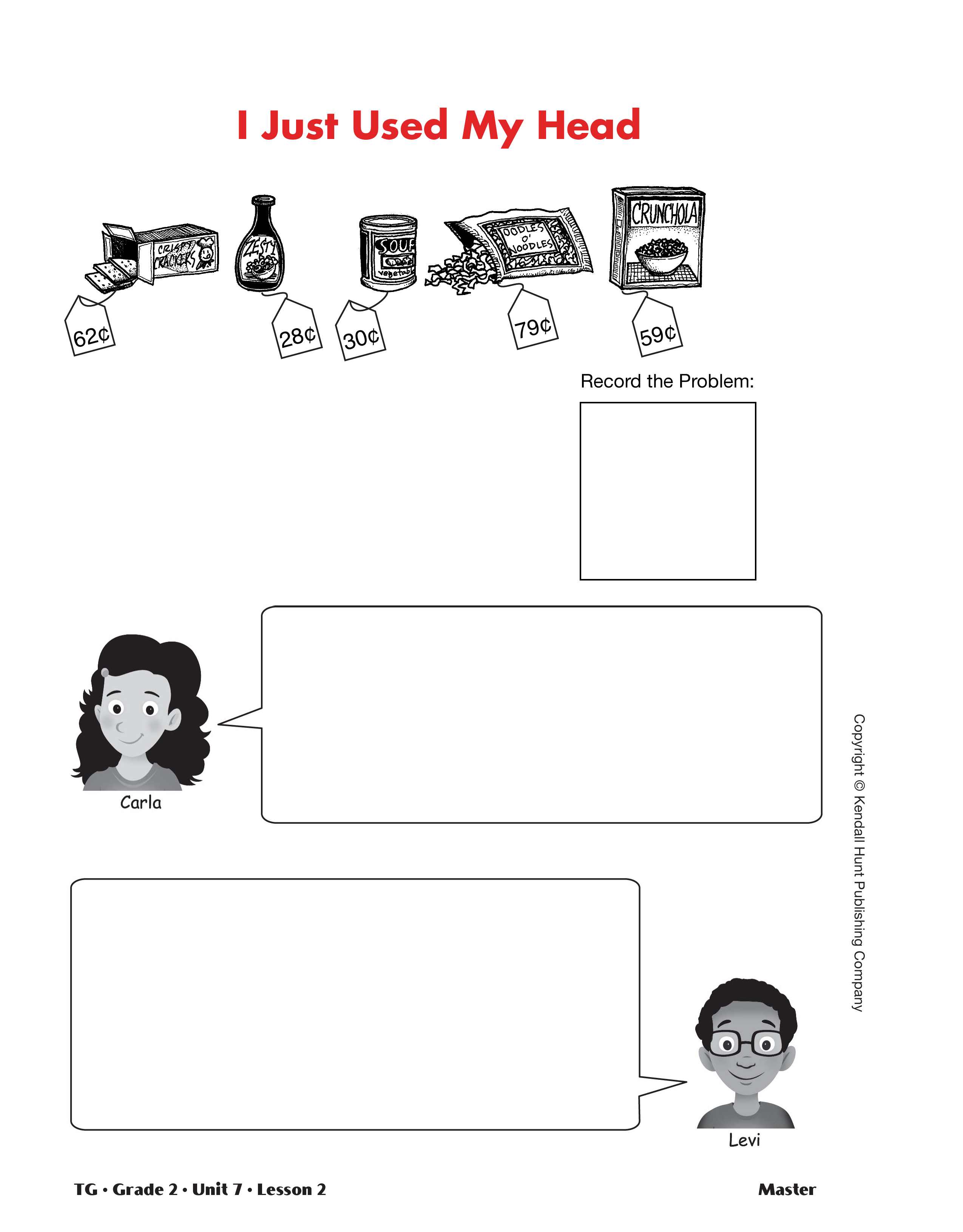
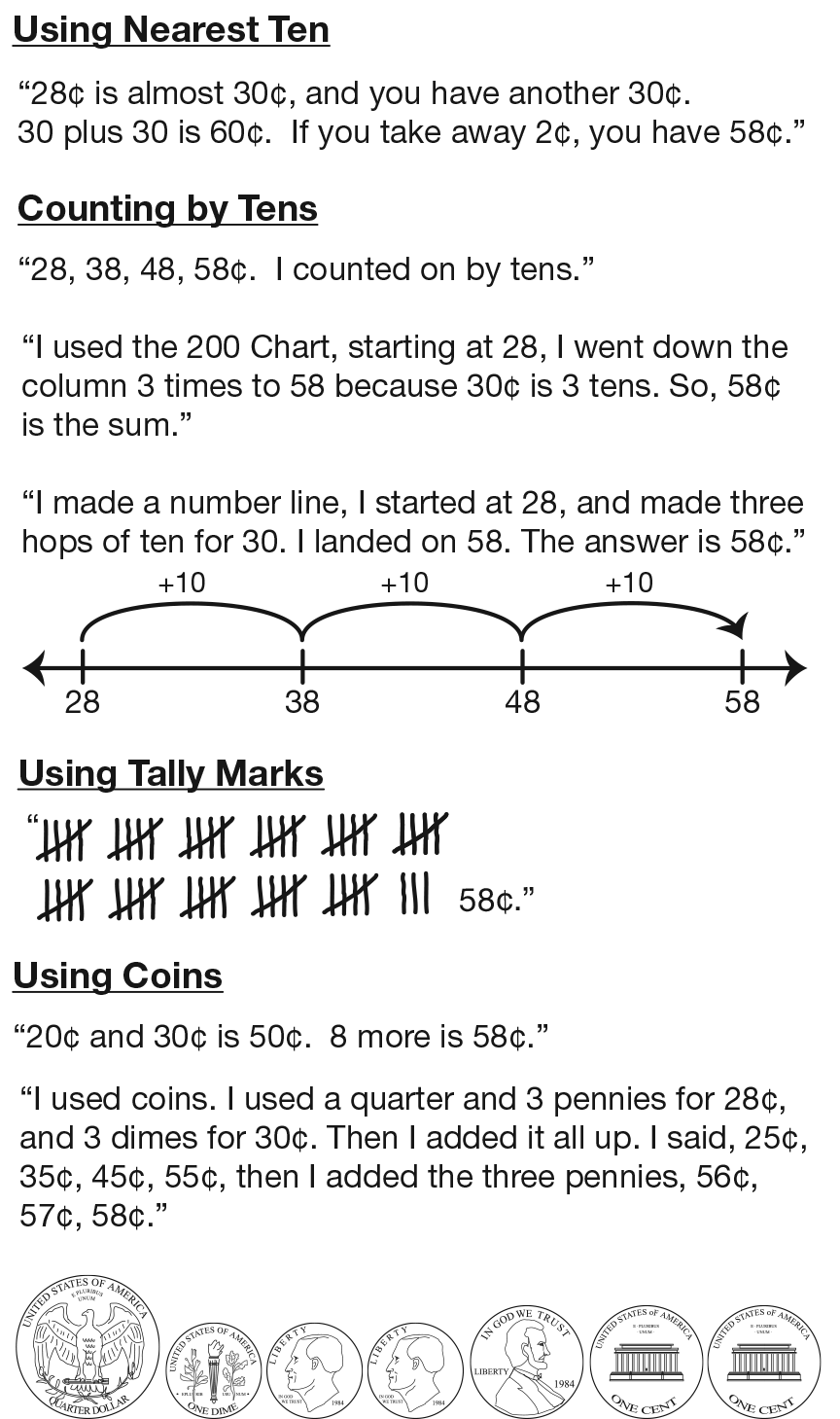
Use Different Addition Strategies. Display the I Just Used My Head Master and the Addition Strategies Chart made earlier in the lesson. Ask students to choose two items to buy and use one of the strategies on the chart to solve the problem. Use the speech balloons to record the thinking of individual students and to list the strategies students use to solve the problems. Encourage students to develop other strategies as they work and add them to the new chart. Discuss whether each student’s answer is reasonable using estimation strategies from Lesson 1. For example, to estimate the sum of 28¢ + 30¢, students might use the friendly numbers 30 + 30 to estimate a sum of 60. See Figure 2 for some solution strategies that might be suggested for adding 28¢ and 30¢.

Choose two new items on the I Just Used My Head Master and repeat the process. Encourage students to try a strategy from the chart that they have not used before. Add any new strategies to the chart.

Compare the strategies by asking questions similar to the following:

How is counting by tens like using the number line? (Possible response: We go up by tens in both strategies.)
How are they different? (Possible response: I do one in my head and the other I do on the number line.)
[Student name] used coins to solve his problem. Find 26¢ + 45¢ the way [Student name] did it.
Try solving the problem using the number line.

Use Invented Strategies to Solve Word Problems. Have students complete the Olympic Field Day Problems in the Student Activity Book to provide further practice using strategies to solve addition problems. Tell students that a school had an Olympic Field Day and students competed in different activities on the school playground. Encourage students to use strategies on the Addition Strategies Chart or other reasonable strategies. Tools such as the number line, 200 Chart, connecting cubes, and base-ten pieces should be readily available.

Upon completion, have students share their solutions for each problem and add strategies that are not listed on the chart.

ADVENTURE BOOK:

Student Activity Book: 325 327 328

Answers