Look around You and Count

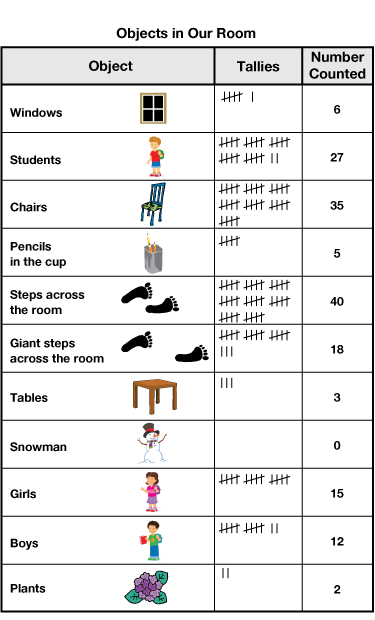
Introduce the Data Table. Tell students you are going to share a counting poem with them called "Look around You." They will be counting items in the poem and in the classroom. Display the Objects in Our Room data table you prepared. See Materials Preparation and Figure 1. Introduce the data table as a helpful tool on which the data you collect can be recorded and organized. Point out the title of the data table, Objects in Our Room. Point out the headings for each column: Object, Tallies, and Number Counted. Explain that tally marks are a quick way of keeping track of numbers. One mark stands for one object. When there are four marks, the fifth number is shown by drawing a diagonal line across the first four marks.

Read and Discuss the Poem. Look around You is a poem in the Adventure Book. Present it in the same way you would any rhyming book. Each verse poses a counting question that should be answered when it is asked. Give students time to count, discuss, and agree on their answers. One possibility is to point to the objects on the page while the class counts aloud. Another is to have one or two students do the activity the poem describes as the rest of the class counts. Or, to better assess individual students, ask volunteers to demonstrate how they count. Read each page aloud and use the corresponding discussion prompts to guide the lesson:

Page 3

Point to each window with a pointer or a meterstick as the class counts aloud. If your classroom door has a window, count it as well.

Collect and Record Counting Data. Record the number of windows counted with tallies and ask a student to write the number on the data table. A completed sample table is shown in Figure 2.

Page 4

Listen to all proposed methods and decide through discussion which ones to attempt. One way is to have a student point to each chair while the class counts aloud. Give students time to count and agree on their answers. This will likely involve numbers beyond ten and is a good opportunity to discover how high some individuals can count.

Have students count the number of chairs in the picture. Some students may count by ones and some may count by twos. Display this number so that they will remember it. This will not be recorded on the data table because it does not pertain to your classroom. Have students count the number of students in the classroom and record it on the data table and also near the displayed number of chairs as shown in Figure 3. Compare the two numbers, making sure students make the connection between the symbols representing each number and the actual items. Point to the numbers on the classroom number line.

To check the answer, call out the names of students as you or the students point to each chair in the picture. As a student's name is called that student may raise his or her hand. If every student's name has been called, then enough chairs are in the picture to seat the class.

Compare Numbers Using More or Less. Allow students to share their strategies for finding the answers to the following questions. Some may help you determine whether students use a counting-on strategy.

Page 5

Show students the cup you have filled with pencils.

Record the number of pencils on the data table. You may wish to fill several cups, each with a different number of pencils and ask individual students to demonstrate counting the pencils.

Page 6

Make Predictions. Try to determine what a typical step (not a big step; not a little step) would look like. Use the steps of the boy in the picture to help guide your discussion. Students may decide to take steps that are heel to toe, heel to toe. Once you choose the step size, remind students to keep it the same when counting. One student may take steps across the room while the rest of the class counts, or the class can take the steps and count together. Record this information on the data table displayed.

Before students take giant steps, ask them to write their predictions down on a small piece of paper. Write your own prediction down without showing the students. Have students count the actual number of giant steps and write that number next to their prediction. Repeat the same process you used before when counting typical-size steps. One student may take steps across the room while the rest of the class counts, or the class can take the steps and count together. Record this information on the data table.

Use the Number Line to Compare. Show the class your prediction for the number of giant steps. Find this number on the class number line. Then find the actual number of giant steps on the number line. Explain to students how you can use the number line to determine if your actual number was more or less than your predicted number.

Ask students to compare their predictions to the actual results. Have them refer to the number line as needed to check their predictions. Ask a volunteer to find his or her predicted number and the actual number on the number line.

Ask students to consider the data they collected when they took normal-size steps across the room. The class can make a prediction of which takes more steps and then count the actual number of steps to compare. Remind students to again use normal-size steps so that they can make an accurate comparison.

Page 8

At the end of the poem, students are invited to look around for other objects to count, but first refer to the objects in the picture. This is a good opportunity to assess whether students are able to identify the quantity of a small group of objects without counting.