Gzorp

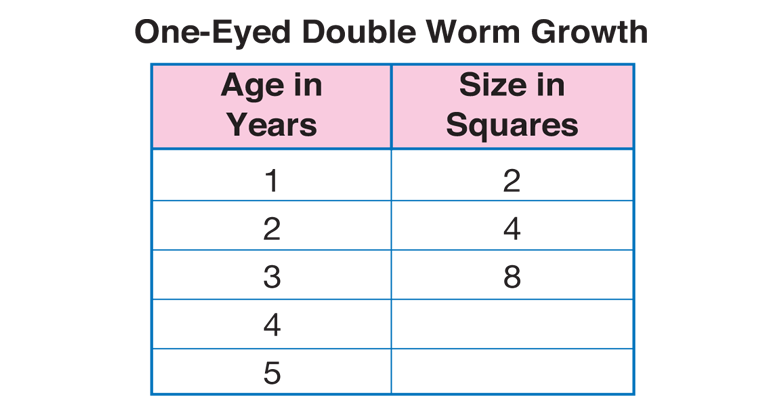
One-Eyed Double Worm Growth Patterns. Explain to students that some creatures on Gzorp grow really fast. One of these creatures is the double worm. There are many kinds of double worms on Gzorp. Every kind of double worm doubles its length each year. Use a display of the first Double Worm page in the Student Activity Book to introduce the One-Eyed Double Worm. Have students use square-inch tiles to model the One-Eyed Double Worm.

Have students add 1 square to the worm to show its length after one year.

Have students add 2 more squares to the One-Eyed Double Worm so that it has 4 squares. Create a data table showing this growth pattern. See Figure 4.

Continue to tell lengths for the One-Eyed Double Worm for various years. Each time, record the length in the data table. See Figure 4. Have student pairs complete Questions 1–3 on the Double Worm pages in the Student Activity Book.

Five-Eyed Double Worm. Display five adjoining square tiles in a row. Explain to students that this is a newborn Five-Eyed Double Worm that starts with 5 squares.

Add 5 squares to the worm to show its length after one year and encourage students to do the same.

Have students work in pairs to develop strategies for solving the problems. Possible strategies include:

• Draw squares to make the worm.
• Use a data table.
• Use the compact method.
• Use a calculator.

Have students demonstrate their strategies for finding the length of a Five-Eyed Double Worm after five years.

Assign Double Worm Check-In: Questions 4–7 in the Student Activity Book to assess students’ abilities to find the length of a Three-Eyed Double Worm at different ages.