Patterns in Data
Number Patterns
This unit covers a broad range of content that enables teachers to assess students’ progress on a … read more
Number Patterns
This unit covers a broad range of content that enables teachers to assess students’ progress on a variety of skills and concepts. It engages students in thinking about and using patterns in two different ways. The first lesson involves patterns in data. These activities model collecting data for a survey of people or about animals. The variable of interest is family size. Since we cannot go into the rain forest and collect data on the family size of animals, we first do it vicariously with the Robinson family in the Armadillo Families Adventure Book story. This story is about collecting data on the number of young in armadillo families. Following the story, students conduct their own survey of the number of children in their families. In class discussions and work with partners, students make decisions about how to collect and display the class data and how to analyze and evaluate it to answer questions. The teacher should serve as a guide and resource person as students make as many decisions as they can.
The teaching suggestions for the lab are based on observations of methods teachers have used successfully to implement each step of the TIMS Laboratory Method. However, they never represent the only acceptable approach. There is much to be learned from providing students with opportunities to make reasonable problem-solving decisions of their own. The ultimate goal of this unit is for students to begin to see the scientific method as a useful tool for finding answers to their own questions. One second-grade student illustrates this point well: Jane was curious about how many different kinds of birds were visiting the feeder in her backyard, so she independently made a data table and graph to show how many of each kind of bird visited.
In Lessons 2 and 3 students look at number patterns. In mathematics a function is a rule that assigns to any input number exactly one output number. In Lesson 3 Rule Machines, students explore “machines” that change numbers according to a fixed rule or pattern. Each machine takes a number, called the input, changes it according to its rule, and emits a new number as its output. For example, the doubling machine outputs the number that is two times the input number. In this lesson students also work with the halving machine and with machines that add or subtract a fixed number. Work with these machines serves several purposes. At the most basic level, it helps students reinforce and extend their experiences with the four operations. More importantly, the lessons deal with recognizing and describing numerical patterns. These concepts are essential building blocks for understanding algebra.
Lesson 3 Gzorp introduces an imaginary world where animals are made out of unit square “cells.” These animals grow according to certain rules. Counting the number of cells in an animal every “year” gives rise to a variety of patterns. Students find this to be an engaging context in which they develop their skills at identifying, describing, and using patterns to make predictions.
Coordinates
Several major ideas related to coordinates are presented in this unit. First, Mr. Origin visually depicts the notion that … read more
Coordinates
Several major ideas related to coordinates are presented in this unit. First, Mr. Origin visually depicts the notion that directions—right, left, front, back—depend on choosing a reference point. Second, concepts of relative size and placement of objects can be developed by reading and creating maps. Third, locating an object on two perpendicular axes provides the foundation for measuring in a two-coordinate system. Finally, the distance between objects can be measured on a scale map.
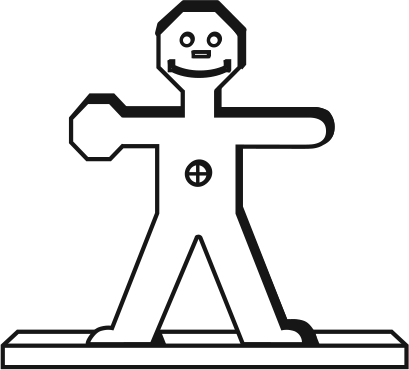
Figure 1: Mr. Origin
Locating an object on a flat surface by using two numbers, called coordinates, is an idea dating back to the seventeenth century. One story (which may not be entirely factual) tells how French philosopher and mathematician René Descartes originated this idea. He had a daily habit of lying in bed until noon while he thought about his current philosophical or mathematical problems. One morning, he was working on a particularly difficult problem: how to use numbers to describe the position of an object. As Descartes gazed at the tiled ceiling, he saw a fly crawling in a jagged path. Suddenly, he had a flash of inspiration. If he chose one point, now called the origin, he could describe the fly’s position with respect to this reference point by using two numbers: the number of tiles the fly was to the right or left of the origin, and the number of tiles the fly was to the front or back of the origin.

Figure 2: Descartes describes the fly’s location
Descartes used his insight to create a system for locating objects without a need for ceiling tiles. Instead, all that is needed is an origin and perpendicular axes; the tiles are “imaginary.” In honor of Descartes, locating objects this way is now known as Cartesian coordinates. Mathematicians generally label the horizontal axis the x-axis and the vertical axis the y-axis. In this unit, we call the horizontal axis the left/right axis and the vertical axis the front/back axis.
MATH FACTS and MENTAL MATH

Subtraction Facts
Daily Practice and Problems items in this unit can be … read more
Subtraction Facts
Daily Practice and Problems items in this unit can be used to assess students’ fluency with the subtraction facts related to the addition facts in all groups.












