In this lesson, students collaborate to invent strategies to solve division problems. It is important to allow students freedom to invent, test, and revise their own strategies for solving division problems, even if their initial strategies appear inefficient. This freedom allows students to enter the task by using their own (and their peers') initial understandings about division.
At this point, encourage students to use methods that do not involve an established algorithm for division. Some of these algorithms will be used later in the unit after the underlying concepts have been developed. Using this lesson to observe the methods students invent freely provides valuable information about their current understanding of division concepts.
Use Efficient Strategies to Count Out Large Numbers. For this lesson arrange students in groups of four. Students combine their collection of centimeter connecting cubes so that each group has at least 160 centimeter connecting cubes available to solve each problem. Begin by asking students to count out 146 cubes. Have groups check the accuracy of their count by having two or three group members verify that there are 146 cubes. Note the strategies students use to count out the cubes. Do they count each cube individually? Do they count by 2s, 5s, or 10s?
Use the following discussion prompts to help students share their strategies for counting out a large number of items.
- What strategy did you use to count out 146 cubes? (Strategies will vary, but should include grouping the items and using skip counting.)
- If your strategy was to count out 146 connecting cubes using groups of 2, what did you notice? (Since 146 is an even number, you can count by twos and get to146.)
- If you used counting by 5s as your strategy, what did you notice? (When you count by 5s, you can count to 145, but then you have to add one more connecting cube to total 146.)
- If your strategy was counting by 10s, what did you notice? (You can count by 10s up to 140, but then you have to add 6 more connecting cubes to get to 146.)
- What strategies do you think are most efficient for counting out a large number of cubes? (Strategies will vary. Some students may identify grouping the cubes and counting by 5s or 10s as most efficient, while others might think this could lead to more error and prefer counting by 2s. What is most important is that groups check for accuracy by recounting each group of cubes before solving each problem.)
Invent Strategies to Divide Large Numbers. As a class, read Question 1 in the Inventing Ways to Divide pages in the Student Guide.
- What is the problem asking? (How many treats will each dog get?)
- What information do we know that will help us solve the problem? (There are 138 treats total. There are 4 dogs. Each dog should get the same number of treats.)
- What tools can we use to help us solve the problem? (connecting cubes, paper, and pencil)
Before groups begin to solve Question 1 make sure they assign one person to be the recorder.
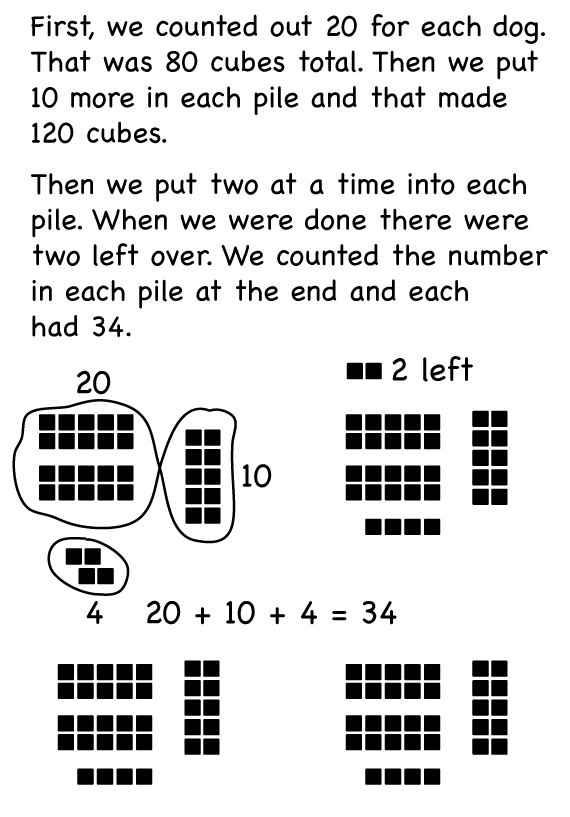
Students solve the problem while the recorder keeps a detailed log of what the group is doing. Suggest to the recorders that they draw pictures to represent the group's solution. Figure 1 shows one possible strategy for solving the problem. Because the intent of these problems is for students to invent strategies for doing division, calculators should not be used.
After completing the problem, ask two or three groups to explain to the class how they solved the problem. You may wish to have these groups record their work onto chart paper for easy display. Try to choose groups that represent a range of approaches. For example, some groups may use simple counting strategies while others may invent mental math strategies. All are worth displaying.
- How many treats does each dog get? (34)
- How did you find your answer? (See Figure 1 for a possible solution.)
- Are there any treats left over? How many? (There are two treats left over.)
If students think of dividing remainders using simple fractions like 1/2 or 1/4 , encourage them to explore this idea. Understanding the concept of evenly distributing remainders across groups will help students interpret the meaning of decimal quotients when they use a calculator or mixed-number quotients when they encounter them. If students are not ready to make sense of this concept, however, focus on helping them understand and interpret whole-number remainders first. Opportunities to develop the concept of fractional quotients will arise in the future.
Discuss with the class the meaning of the remainder by asking:
- Why are they left over? (Possible responses: You cannot give the last two treats away because not every dog will have the same number of treats. The remaining treats can be split in half so that each dog gets another half of a treat. See Meeting Individual Needs box.)
- Are there always going to be leftovers when dividing numbers equally? (No.)
- How could you change the problem so that there are no doggie treats left over? (Possible responses: If you began with two fewer treats—or 136 treats—each dog would still get 34 treats but there would be none left over after dividing equally. If there were 140 treats at the start, each dog would get 35 treats with none left over.)
Have students put the cubes back together in a single pile of 138 and assign a new recorder. Read Question 2 with the whole class.
- What is this problem asking? (How many treats will each dog get?)
- What information do we know that will help us solve the problem? (There are still 138 treats total, but now there are five dogs to share the treats equally.)
Ask students to solve this problem using a different method from the way they solved Question 1. Again, have two or three groups share their methods with the class.
After each group assigns a new recorder, read Question 3 with the class.
- What is this problem asking? (How many boxes are needed for all the cookies?)
- What information do we know that will help us solve the problem? (There are 116 cookies. Each box holds 8 cookies.)
- How is this problem the same as the problems in Questions 1 and 2? (All the problems involve division of a three-digit number by a one-digit number.)
- How is this problem different from the problems in Questions 1 and 2? (The most important difference is that in Questions 1 and 2, the number of groups was known [the amount of dogs], but not the number of objects in each group. In this question, the number of objects in each group [number of cookies in each box] is known, but the number of groups [cookie boxes] is not known. See Content Note.)

Types of Division. The type of division called for in Questions 1 and 2 is known as partitive division. Here, the number of groups is known but the number in each group is not, as with equal sharing. In Question 3, the problem presents a case of measurement division, where the number in each group is known and the number of groups is what needs to be found. A third type of division, known as comparison division, occurs when two set sizes are being compared (e.g., How many times as many apples are in Basket A as in Basket B?) Students need not know and use these terms at this point, but they should become familiar with all three contexts so they can make sense of all the meanings of division.
Have students use the connecting cubes to solve the problem in Question 3 with their groups. Because this problem involves measurement division, students' strategies may be less varied. Students will typically collect the cubes into groups of 8 and count the number of groups. Pay attention to variations in strategies. Select one or two groups to show their solutions to the whole class.