Modeling Division

Est. Class Sessions: 2

Developing the Lesson

Part 2: The Rectangle Model

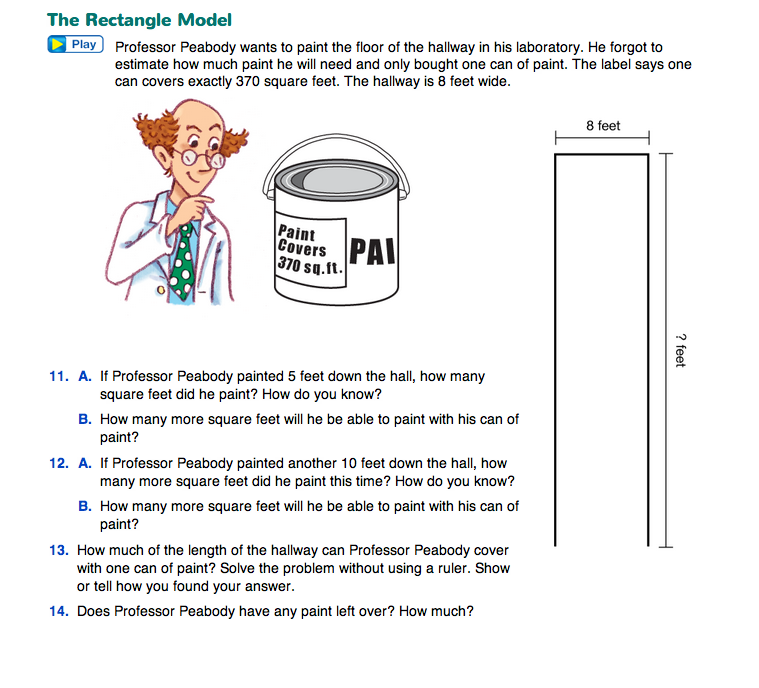
Ask students to read the introductory problem in the Rectangle Model section in the Student Guide. This problem establishes a model for solving division problems based on the rectangle model for multiplication. The key difference is that, in the case of division, the area and one of the side lengths of the rectangle are known and the other side length is the quantity to be found.

In this problem, a quantity of paint is known to cover a given area (370 sq. ft.) in a hallway. The width of the hallway is also known (8ft.), but the length of hallway that can be painted is not. In this context, the area represents the dividend, the hall width represents the divisor, and the unknown length represents the quotient. See Figure 2.

Questions 11–12 help students picture the situation in this context. After students have answered and discussed these questions, ask them to solve the problem as posed in Questions 13 and 14 before looking at Professor Peabody's solution on the following page.

Questions 11–12 provide an opportunity for you to determine whether students understand the problem context or not. The context itself may be unfamiliar to some students. Students may also have difficulty transferring what they know about area to a division problem. These questions can help students develop a mental picture of what the Professor Peabody problem involves.

Have students draw the diagram and encourage them to use it to solve the problem.

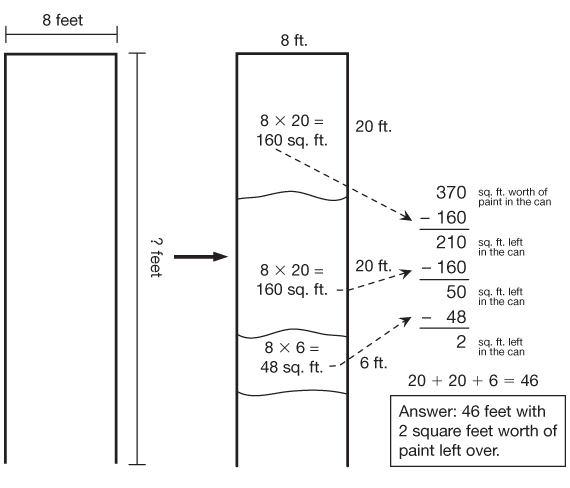
After allowing students sufficient time to work on the problem, read through Professor Peabody's solution together. Have students discuss with a partner how their solutions compared to Professor Peabody's (Question 15).

Ask students:

Did you get the same answer as Professor Peabody?
How was your solution different from his? How was it the same?

Use Questions 16–18 to help students make sense of Professor Peabody's solution. Questions 17 and 18 deal specifically with the meaning of the remainder. It is important for students to understand that for the procedure to be complete, the remainder must be less than the divisor. If it is not, another partial quotient is possible and the division should continue. One possible explanation of the remainder for Question 18 is that there is enough paint left in the can to cover 2 square feet. That is not enough to paint another whole foot across the width of the hallway because that would take another 8 square feet of paint. Students may suggest that Professor Peabody use up all the rest of the paint anyway. It would get him a little further down the hall but not a whole foot further.

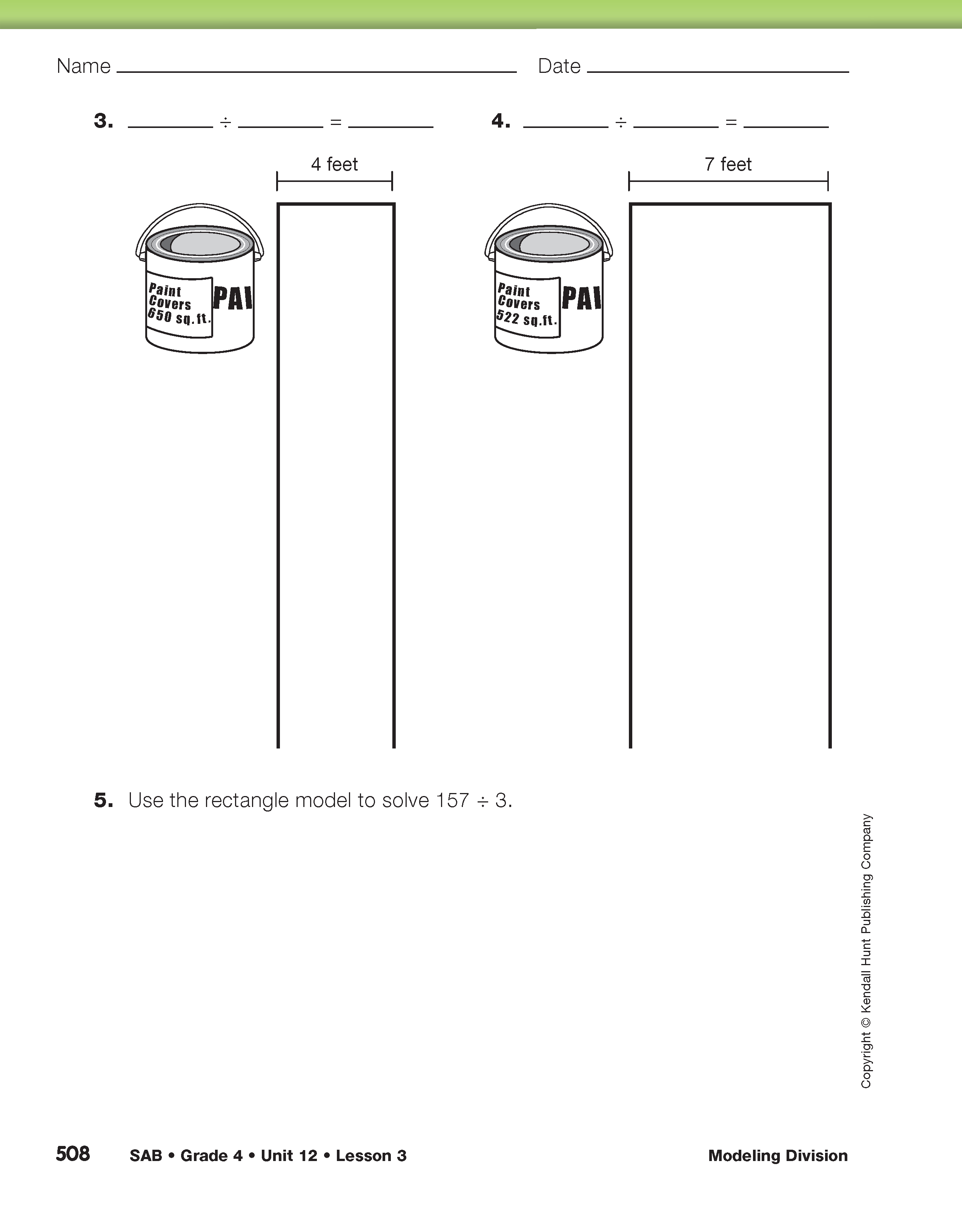
Have students complete the How Far Down the Hall? pages in the Student Activity Book to practice using the rectangle model to solve division problems with single-digit divisors.