Workshop: Division Concepts

Ask students to turn to the Game Rules section of the Quotient Quest pages in their Student Activity Books. Draw or display a game board as shown in Figure 1, and ask students to play along using their own Quotient Quest Game Boards from the Student Activity Book.

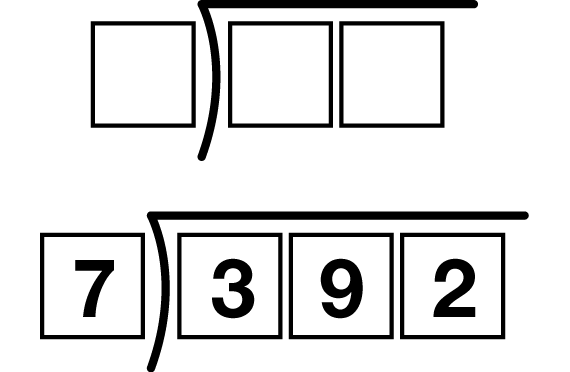
Ask students to place their 20 Quotient Quest Digit Cards in front of them as you demonstrate the game. Draw a card from the Quotient Quest Game Cards and read the card aloud. The goal is to place digit cards into either set of boxes to make a quotient that matches the game card. For example, if the game card reads, “Divide to get a quotient between 50 and 60,” digits may be placed into the boxes as shown in Figure 2.

This quotient matches the card because 392 ÷ 7 = 56, which lies between 50 and 60. There are many other quotients that match as well.

Students may use a variety of strategies for finding quotients that match a given game card. Figure 3 shows a student's possible line of thinking for finding the quotient shown in Figure 2 if they have only digit cards with 2, 3, 7, and 9.

Students may use calculators to check quotients, but encourage them to use multiplication and mental math strategies first. See the Meeting Individual Needs box.

It is important to note to students that in this example, a quotient of exactly 50 or 60 would not match the card because it does not lie between 50 and 60. Once a quotient has been verified, demonstrate removing the digit cards from the board and placing them on a discard stack. Explain that the object of the game is to get rid of digit cards this way and to have the lowest sum of digits on your remaining digit cards at the end of the game. Draw one or two more game cards to further demonstrate playing the game.

Note whether students are using multiplication and estimation strategies to find quotients that match the game cards. After demonstrating a few more turns, review with the class the Quotient Quest Game Rules section in the Student Activity Book.

Have students play the game in pairs as you monitor their use of estimation and multiplication strategies. The following variations on the game can be introduced as needed:

Variation 1:

Deal 10 digit cards per player instead of 20 to shorten the game.

Variation 2:

Introduce a modified game board that includes a 4-digit number divided by a 2-digit number for students who are ready to explore estimation with more complex quotients.