Lesson 6

Paper-and-Pencil Division

Est. Class Sessions: 2–3

Developing the Lesson

Part 1. Exploring the Partial Quotients Method with an Area Problem

Solve a Problem Using the Partial Quotients Method and the Rectangle Model. As a warm-up activity, ask students to solve the problem below, which is similar to problems in the Student Activity Book in Lessons 3 and 4.

  • Professor Peabody wants to paint the floor of a hall that is 8 feet wide. The label on his can of paint says he has enough to cover 280 square feet. How far down the hallway can Professor Peabody paint with the amount of paint he has?

Draw a picture of the hallway as in Figure 1 and encourage students to solve the problem by making and refining estimates as they did before. They can record their calculations any way they want. Explain that after they solve the problem, you will talk about an organized way to record their calculations.

After students have solved the problem, ask a volunteer to share his or her solution. As the student describes the estimates in his or her solution, show how to record the same estimates in the partial quotients method. Figures 2–4 show each step as a student might write it using the rectangle model and the comparable step as written in the format of the partial quotients method.

In Figure 2, the first estimate is 10 feet. Multiplying 8 × 10 = 80 shows that after painting 10 feet down the hall, 80 square feet of floor have been painted. Write 80 under 280 and subtract. There is enough paint remaining to cover another 200 square feet.

Figure 3 shows a second estimate of 20 feet. Multiply 8 × 20 = 160, write the product under the 200, and subtract. There is enough to cover 40 more square feet.

Figure 4 shows a third estimate of 5 feet. Multiply 8 × 5 = 40, write the product under the 40, and subtract to get zero. We stop here—all the paint has been used. Adding the numbers on the right, the partial quotients, we see that 10 + 20 + 5 = 35 feet of hall were painted. We write the quotient 35 on top of the original problem so it can easily be seen.

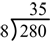
Compare Methods. Ask students to compare the rectangle model with the partial quotients method.

Ask:

X
  • What do you notice that is the same about the two methods? (In both methods, estimates are made and then added to find the answer; after each estimate, the estimate is multiplied by the divisor and then the product is subtracted from the dividend to determine how much is left to be divided; then the steps are repeated with what is left.)
  • What do you notice that is different? (The way it is written looks different; the rectangle model shows the multiplication step and the partial quotient method shows the subtracting step.)
  • Can the same estimates be used with both methods? (Yes)
  • Do the two methods reach the same answer? (Yes)
X

So that students can concentrate on the division concepts in this lesson, students should have multiplication tables such as Facts I Know charts readily available to help them with their facts.

X

Ask students to record both strategies on their papers or put students in pairs and ask one to record the partial quotients method and the other to record the column method.

Student Guide:
Student Activity Book:
Master:
Setting up the problem
X
+
First estimate: 10 ft.; 8 ft. × 10 ft. = 80 sq. ft.; eaves 200 sq. ft. to paint
X
+
Second estimate: 20 ft.; leaves 40 sq. ft. to paint
X
+
Third estimate: 5 ft.; no paint remains
X
+