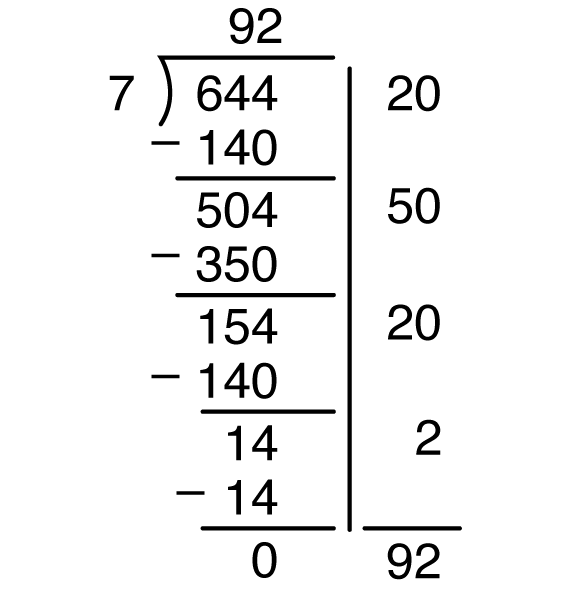
Solve a Problem Using the Column Method. Another way to think about division is with a sharing problem.
Pose the following problem and begin to solve it together:
A box contains 644 beads. If the beads are to be shared equally among 7 children, how many beads will each child get?
Ask students if they recall a similar problem from recent lessons. They should recall that in the opening problem in Lesson 4, a collection of rocks was shared among 5 students.
- What method did we use to solve that division problem? (We drew columns to keep track of the rocks as we were dividing them up.)
- Would that same method work to solve this problem? Why do you say so? (Yes, because in both problems we are taking a group of things and sharing them equally among a number of people.)
- How many columns should I draw for this problem? Why? (7 columns because the beads are divided up among 7 children.)
Ask students to estimate the answer:
- Will each child get more than 100 beads? Tell me your thinking. (No, 100 is too high since 7 × 100 = 700.)
- Estimate. What is a reasonable guess for the number of beads each student will get?
Write student estimates on the board to be checked after the problem has been solved completely.
Solve a Problem Using the Column and the Partial Quotients Methods. Ask students what amount they would choose for an initial distribution of the beads. Suggest using small, convenient numbers (numbers ending in zeros are good) at the beginning. Figures 5 and 6 show 20 as a first estimate, then 50, then 20 again, and finally 2.
As you work through the problem with the class, have a student write the estimates and calculations in the columns as you write them in the partial quotients format. Ask students to suggest possible estimates and ask them to explain what each number in the problem represents.
- Tony has suggested 20 for the first estimate. What does that 20 mean? (The 20 means that we give each child 20 beads.)
- Where did we write the 20 in the column method? (We write a 20 in each of the columns to show that each child got 20 beads.)
- Where did we write the 20 in the partial quotients method? (At the right of the problem.)
- How many beads total have we shared so far? How do you know? (140 beads because we gave 20 beads each to 7 children. 7 × 20 = 140.)
- Where did we write the 140 beads in the columns method? (At the right, under the words “Into the columns.”)
- Where did we write it using the partial quotients method? (Under the dividend, 644.)
- How many beads do we have left that still have to be shared? How do you know? (We have shared 140 so we subtract: 644 beads to start minus 140 beads = 504 beads left to share.)
- Where do we write that in our two methods? (In the column method, it is written at the right. In the partial quotients method, the subtraction is shown under the dividend.)
- We have 504 beads left to be shared. How many should we distribute in the next step? Who can suggest another estimate?
- Estimate the number of times 7 goes into 504.
In this example we estimate that 7 goes into 504 fifty times. Then multiply 50 times 7 to get 350 and subtract. There are now 154 beads left to be distributed. We continue in this manner until no more beads can be distributed.
Continue to ask students what each number means.
- What does the last number sentence, 14 – 14 = 0, tell us? (It tells us that we have no more beads. We have shared them all.)
- How many shares or equal groups did we make? How many children received beads? (7 children received beads.)
- How many beads did each child get? How do you know? (Each child got 92 beads; I know because I added up how many we gave in each step. 20 + 50 + 20 + 2 = 92.)
- Were there any beads left over? How do you know? (There were no beads left over because at the end we had 14 beads and gave 2 to each child and that took care of all the beads. 7 × 2 = 14; 14 − 14 = 0 beads.)
Compare Methods. After finishing the problem, write the quotient (92) above the dividend as usual. Have students make comparisons between the two methods as before.
- How are the two methods alike? (They both have the same steps: making an estimate, subtracting the product of the estimate and the divisor from the dividend, making a new estimate, etc., until there is nothing left of the dividend to be divided; then all the estimates are added to find the answer.)
- How are the two methods different? (Using the columns, we write the estimates from the bottom of the column and move up; with the all partials, the work is from top to bottom. The column method has a lot written at the right side, but the partial quotients method has only the partial estimates written on the side.)
- How can you check your answer to see if it is correct? (Using multiplication)
Students can check the answer by multiplying to see whether the quotient times the divisor gives the dividend, the number they started with. That is, to check that 644 ÷ 7 = 92, check that 92 × 7 = 644.
Use Partial Quotients. Use the partial quotients method with several more problems:
448 ÷ 8 (Answer: 56)
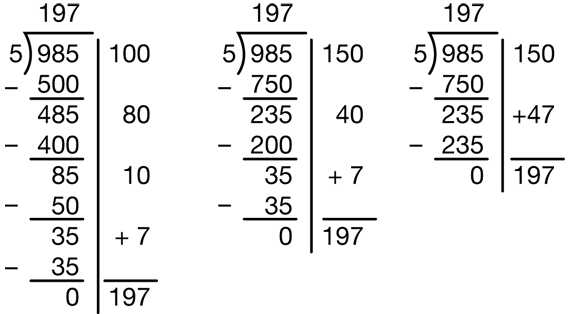
985 ÷ 5 (Answer: 197)
756 ÷ 9 (Answer: 84)
For each problem, ask students to estimate their answers first. For example, 448 ÷ 8 is less than 60 since 8 × 60 = 480. It is more than 50 since 8 × 50 = 400. For the second problem, they can easily see the answer is more than 100 since 5 × 100 = 500 and it is less than 200, since 5 × 200 = 1000.
While the class is solving the problems, look for students who solve a problem using different estimates and therefore a different set of steps to complete the problem. Ask the selected students to record their solutions on the board side by side. See Figure 7.
Discuss similarities and differences in the steps:
- What do you notice about the steps in the solutions? (In the examples shown, one solution has 4 partial quotients, one has 3, and one has 2.)
- Why was one student able to do the problem in fewer steps? (He or she selected larger estimates.)
- Which strategy seems most efficient? (Students may select the strategy with the least steps. Some students will choose the strategy where they can do the multiplication easily in their heads. Either response is acceptable.)
Solve Problems with Remainders.
Present an example with a remainder:
A bakery made a batch of 549 cookies. They sold the cookies in packages of 8. How many packages of cookies did they make?
Begin by asking students to estimate the number of packages:
- Will the number of packages be over 100? Over 50? (There will be less than 100 packages because 8 × 100 = 800. There will be more than 50 packages because 8 × 50 = 400.)
Ask students to solve the problem and share one or two solutions with the class. A sample solution is shown in Figure 8. The discussion prompts in Figure 8 are adapted from a classroom discussion in which the teacher checked for students' understanding of the steps in the partial quotients method.