Developing Flexible Models and Methods

Students who develop conceptual understanding of operations make fewer errors, retain learning longer, approach problems with confidence, and apply flexible strategies to new problem situations. In Units 3, 4, 7, and 11, students developed a conceptual foundation for understanding multidigit multiplication through the use of the rectangular array model, estimation, and mental math strategies. These models and strategies provide students with a range of methods to solve problems flexibly. They also allow students to make sense of paper-and-pencil methods for multiplication by linking efficient computation to an understanding of number, place value, and operations.

In this unit, a similar approach is used with division of multidigit numbers by a single-digit divisor. Students use various models and mental math strategies to develop foundational understandings about division. These include estimation strategies, a rectangle model similar to the model for multiplication, a tabular column method that illustrates equal distribution, the use of cluster problems, and the promotion of students' invented strategies that are mathematically sound.

Not only do these methods support sense-making about division, they also build on the connection between multiplication and division as inverse operations (NCTM, 2000; Van de Walle, 2006). Developing multiple strategies gives students the means to choose methods flexibly, so that they can solve different types of problems efficiently, instead of depending on only one method.

The use of paper-and-pencil procedures grows out of the work students do with these less formal strategies. For example, the partial quotients method of long division (discussed below) emerges as a more efficient recording of the computations necessary for the rectangle model. The concrete and pictorial models link directly to more abstract algorithms. The connections among them are clarified through use of the Division Strategies Menu (Figure 1). Additionally, a strong foundation in estimation enables students to use paper-and-pencil algorithms more accurately and efficiently (NRC, 2001). Therefore, it is important to give students ample time to develop the underlying concepts and skills necessary for understanding and doing division by working with the various models and strategies. This is true even if they have already learned a procedure for dividing using a paper-and-pencil algorithm.

Types of Division

Students work with several types of division, all of which are important for an understanding of the basic operation. In one type, the number of groups (partitions) is known and the quotient is the number in each group, as with equal sharing. This type is known as partitive division (e.g., A basket has 32 apples. How many apples will go into 8 bags if they are divided evenly?). Alternately, the number in each group is known and the number of groups is what needs to be found (e.g., How many bags are needed if 32 apples are placed in bags with 4 apples each?). This is typically known as measurement division. A third type of division, known as comparison division, occurs when two set sizes are being compared (e.g., How many times as many apples are in Basket A as Basket B?) (Van de Walle, 2006). While these terms are not discussed specifically with students, each type of division is incorporated in the models that are used and in the way problems are posed.

Partial Quotients Method

In this unit, students learn a paper-and-pencil division method that is somewhat different from the one traditionally used in the United States. This method, called the partial quotients method, does not require that the greatest quotient be found at each step, eliminating the frequent erasing encountered with the standard algorithm. Students who are taught the partial quotients method are better at solving unfamiliar problems and are better able to explain the meaning of the steps and each number in the method than those taught only the traditional method. The partial quotients division method also gives students the opportunity to practice mental math and estimation strategies.

Figures 2–6 show an example of the partial quotient method for dividing 4 into 671.

• There are 671 marbles to be shared equally among 4 children. How many marbles will each child get?

Equally sharing, that is, dividing a quantity equally into a known number of groups, is familiar to children and it forms the basis for the column method used in Lesson 2.

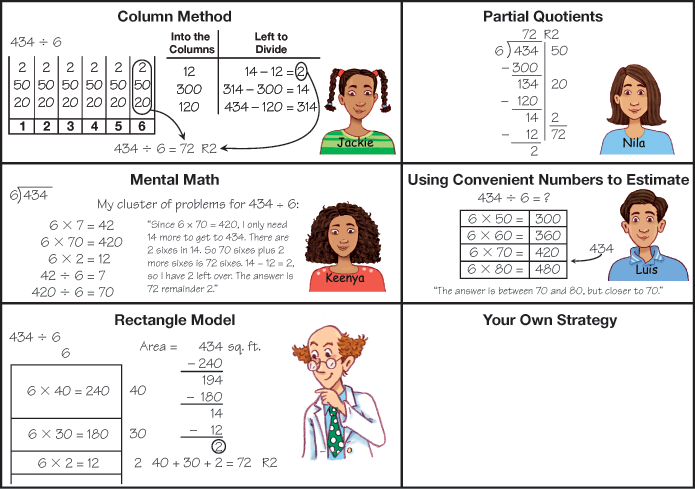
To begin to solve the problem using the partial quotients method, make an intelligent guess, say, 100 for the number of marbles each child will get. Write 100 on the right. Since 4 × 100 = 400, write 400 underneath to indicate that 100 marbles have been distributed to each of 4 children. To see how many marbles still have not been distributed, the 400 is subtracted from 671. This leaves 271 marbles to be further divided.

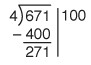
Next, we estimate the number of 4s in 271. Students should see that 100 will not work again because there are no longer enough marbles to give each student 100. A student might choose 10 here as shown in Figure 3. Multiplying 10 × 4 will distribute 40 more marbles, leaving 231 still to be distributed.

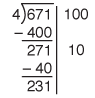
At this point, a student may see that an estimate of ten is small and didn't reduce the number left to be divided by much. A larger estimate is possible. In our example, shown in Figure 4, the next estimate is 20.

The next estimate could be either 20 or 30. A student may decide that there are still enough marbles to distribute 20 to each child again. On the other hand, at this point the student may realize that a larger estimate will make for fewer repetitive steps. With practice, the student will start to recognize the connection between the estimate and the multiplication and division facts. He or she can make an estimate of 30 in the next step because 4 × 30 = 120, which distributes more of the marbles than the estimate of 20 but is still less than the 151 marbles left to distribute. Figure 5 shows both of these possible estimates.

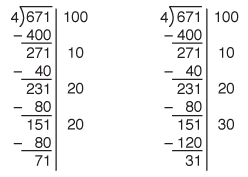
To finish off the problem, the estimates on the right in Figures 5 and 6 allow for solving the problem in fewer steps. The last partial quotient in both examples is 7, leaving a remainder of 3. Adding up the number of 4s that divide 671, we find 167. That is, 4 divides 671 a total of 167 times with remainder 3.

We distributed 167 marbles to each child with 3 left over. The 167 R3 can be written above the problem as usual.

Over time, as students become more fluent with their multiplication and division facts, they become better at mental estimation, and the number of steps required with this method decreases. The partial quotients method closely resembles the traditional method if the best estimate is made at each step. See Figure 7.

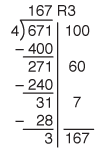
Practice

Practice with multiplication and division is provided in this unit and the Daily Practice and Problems. Researchers find that spending more time in understanding procedures before practicing them aids recall and proficiency in the long run (Hiebert, 1990). Students should practice small numbers of problems for short periods of time throughout the year.

While we have chosen methods to use to teach division, encourage students to share other correct methods of dividing—either those they learned previously, those learned from their parents, or those they invented themselves. Class discussions about other methods can greatly enhance understanding of division and also convey the message that problems in mathematics can be solved in many ways.