Estimating Quotients

Est. Class Sessions: 1

Developing the Lesson

Strategies to Estimate Quotients. Ask students to work in pairs. Assign one or two problems from Questions 1–6 in the Student Guide to each pair. Be sure each problem is assigned to at least one pair of students. After students have had a chance to solve their assigned problems, ask each group to share their problem, the solution, and how they checked if their answer was reasonable.

Some students will estimate using convenient numbers to check for reasonableness and others might estimate using obvious multiplication facts to check their solution. Help students identify and describe the similarities and differences in their solutions.

Ask the class to take a closer look at Question 6 by writing the following problem on the board:

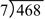
Ask:

How is this problem different from the division problems we have done so far? (Students may respond that there is not an obviously related division fact.)
What is your guess for a number close to the quotient? (Answers may vary; a reasonable answer might be between 50 and 80.)
How can you test if your guess is close to the actual answer? (Multiply the guessed number by seven to see how close the product is to 468.)
What fact families that use 7 will be helpful in finding an estimate? (7 × 6 = 42 and 7 × 7 = 49)
Why are those multiplication facts helpful? (Possible response: If you multiply the products 42 and 49 by 10, you get products close to 468, the dividend in our problem.)
7 × what numbers are close to 468? Why? (468 is between 7 × 60 = 420 and 7 × 70 = 490.)

Using Multiplication to Estimate. These questions lead to a discussion about estimating with division. Tell students that they can estimate answers to division problems by making an educated guess using multiplication facts, fact families, and multiples of 10. Then test the guess using multiplication. The product can then help with making a better guess.

Ask students to refer to the Using Multiplication Facts to Estimate pages in the Student Activity Book. Show a display of the first page. Compare the class's estimates for with the one shown on the page.

Solve the first problem from this page in class together before asking students to complete the remaining problems independently or in groups.

As students think about their estimates to Question 1, ask:

What numbers might you use to estimate the quotient in the problem 536 ÷ 8? (Students should suggest using multiplication facts and multiples of 10 to estimate.)
What fact families will be helpful in estimating 536 × 8? (8 × 6 = 48 and 8 × 7 = 56)
What multiples of 10 would make good estimates to start with? (Possible response: 8 × 50 = 400, 8 × 60 = 480, 8 × 70 = 560)

Students may report an estimate as a single number or as lying within a range between two numbers. Encourage them to do both. For Question 1, a good estimate might be either 70 or a number between 60 and 70. If estimates are given as a range, push students to think about which end of the range the answer lies closer to. Reasonable estimates will also help students find good initial partial products for solving division problems by paper-and-pencil methods in lessons to come.

If students have problems identifying the fact families and corresponding multiples of 10 that are close to the dividend, ask questions similar to these for Question 4, 225 ÷ 3, in the Student Activity Book.

What multiples of 10 are close to 225? (200, 210, 220, 230, 240)
What multiplication facts with 3 will help you find a good estimate? Look on your Facts I Know chart. (3 × 7 = 21 and 3 × 8 = 24)
What multiples of 10 will you use? (3 × 70 = 210 and 3 × 80 = 240)
What is a reasonable estimate for 225 ÷ 3? (A number between 70 and 80)