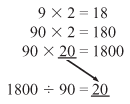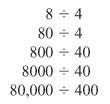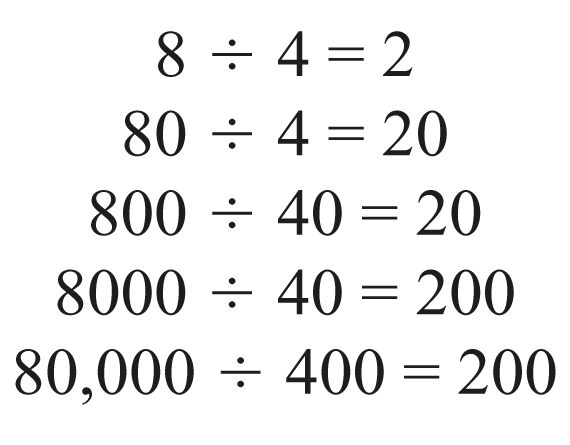Although students have been working consistently with division facts, they have not necessarily thought about division models and concepts recently. Some students may need extra time and support to be able to model division problems using a situation (story) or picture. Students will develop models for division problems in Lesson 3 of this unit, but the following examples may be helpful for struggling students:
- If 28 students are split up into teams of four students each, how many teams are there?
- If 28 cookies are divided equally among four students, how many cookies does each student get?
- How many groups of four are there in 28?

- If 28 is divided into four equal groups, how many are in each group?

- Four times what number is 28? 4 × ? = 28
Use Multiplication. Begin the lesson by reading and discussing the vignette in the Dividing with Multiples of Ten section in the Student Guide. Use the example of Ms. Kay's driving distance as a lead-in for the class discussion on dividing with multiples of 10, and for a brief review of the terms dividend, divisor, and quotient.
Then write the following problem on the board:
28 ÷ 4
Remind students that this is a division problem that also can be written as 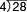 or 28/4 .
or 28/4 .
- What multiplication fact can help you solve this division problem? (4 × ? = 28 or 4 × 7 = 28)
- Write a story or draw a picture to show the meaning of this division problem. Solve the problem and explain your story or picture to a partner.
Have several students share their responses with the whole class.
Now write this problem on the board:
280 ÷ 4
- How is this problem like the first problem? (Responses may vary. Students may say that both are division problems, both have numbers that are divided by 4, both “have a 28 in them.”)
- How is this problem different from the first problem? (The first number, or number you divide [dividend], is ten times larger than the first number [dividend] in the previous problem.)
- What multiplication problem can help you solve this division problem? (4 × ? = 280)
Explain that using multiplication can be a good way to solve division problems. For example, one good way to solve 280 ÷ 4 is to ask, “Four times what number equals 280?”
Ask students to solve 280 ÷ 4, then ask:
- What is the quotient? (70)
- How did you solve this problem? (Possible responses: The answer to the second problem is ten times greater than the first problem [28 ÷ 4] since 280 is 28 × 10. I used a rule for adding zeros when multiplying by multiples of 10.)
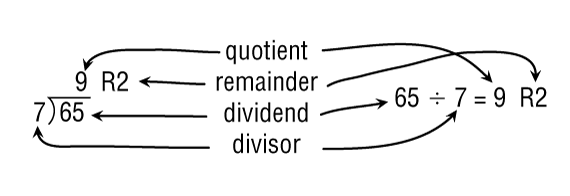
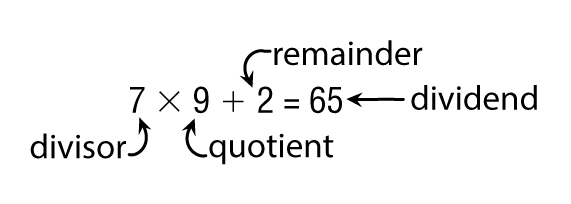
As students become more comfortable with concepts, models, and procedures for dividing numbers, it is useful to use proper terminology when referring to division problems. The number being divided is called the dividend. The number that defines how the dividend will be divided is called the divisor. The resulting quantity is the quotient. When the dividend does not divide evenly by the divisor, some quantity is left over. The leftover quantity is called the remainder. Figure 1 shows each of these components in a simple division problem. Figure 2 shows how the same division problem can be written using multiplication.

Students should have their Division Facts I Know charts or Small Multiplication Tables available so lack of fluency with some facts will not prevent any students from developing the division concepts and skills in this lesson. Use of the tables will build confidence and diminish frustration.
If appropriate, review finding the multiplication and division facts in fact families using the charts or tables.
Now write these problems on the board:
54 ÷ 6
540 ÷ 6
5400 ÷ 6
Ask students to write each problem as a multiplication problem before solving it as shown below.
54 ÷ 6
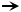
6 × ? = 54
540 ÷ 6
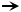
6 × ? = 540
5400 ÷ 6
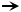
6 × ? = 5400
- What number times 6 equals 54? (9)
- What number times 6 equals 540? (90)
- How do you know that 6 × 90 = 540? (Possible responses: Since 90 is ten times 9, then 6 × 90 will be 10 times 6 × 9, or 540. Or 6 × 9 = 54 and I put on one more zero.)
- What number times 6 equals 5400? (900)
- How do you know that 6 × 900 = 5400? (Possible response: 6 × 9 = 54, and since 900 is 100 times as many as 9, the answer is 100 times as many as 54, or 5400; or 6 × 9 = 54 and I put on two more zeros.)
- What are the answers to the three division problems? (9, 90, and 900, respectively)
Now write this problem on the board:
1800 ÷ 90
- How can this division problem be written as a multiplication problem? (90 × ? = 1800)
- How many 90s are there in 1800? (20)
Students may find this quotient more difficult to find.
- How did you solve the problem?
This division problem is somewhat more complicated than the previous problems since both the divisor and the dividend are multiples of 10. If students continue to think about division problems as multiplication problems with missing factors, they can use their math facts and what they know about multiplying by multiples of 10 to find quotients. Show students how they can use a cluster of related multiplication problems to solve the division problem. Write this on the board:
Develop a rule. Write this set of problems on the board:
Avoiding Misconceptions. Errors in dividing with numbers with zeros at the end can be avoided if students take the time to develop procedures that make sense to them. These procedures should come from well-established concepts of multiplication and division and well-developed number sense. When students can relate procedures to what they know about operations and use their number sense to check for reasonableness, they will make far fewer errors.
It is equally important to avoid teaching procedures that are not mathematically sound. For example, some rules for canceling zeros can lead to errors when computing with fractions or simplifying algebraic expressions.
Ask students to solve these division problems using the strategies they used in the previous problems. Have students check their work using a calculator and discuss their answers with a partner.
- What is the division math fact that we need to know for these problems? (8 ÷ 4 = 2)
- What is the multiplication fact that helps us solve this problem? (4 × 2 = 8)
- What patterns do you see? (The number of zeros in the answer is equal to the number of zeros in the first number [dividend] minus the number of zeros in the second number [divisor]. See Figure 3.)
- Work with your partner to think of a rule for dividing numbers that are multiples of 10.
Some students may resort to rules they have learned about “canceling zeros.” However, students should be able to explain why cancellation works and verify their answers using multiplication.
- Does your rule work for other division problems involving multiples of 10?
If a rule does not work for each of the calculations, it should be revised. This may take several tries. Figure 4 shows two sample rules applied to the problem 2000 ÷ 50 that work all the time for dividing multiples of 10.
Ask a few students to share their rules with the class. Students should test each rule that is presented to make sure it works for every problem.
- Does your rule work for 2000 ÷ 50?
- What is the related division fact? (20 ÷ 5 = 4)
- Why isn't it 2 ÷ 5? (Because 2 ÷ 5 isn't one of our division facts.)
- What does 2 ÷ 5 equal? For example, can I divide 2 cookies into 5 equal pieces? (Possible responses: No, you cannot. Or, yes, you can divide it, but the answer is less than 1, so it is a fraction.)
- What is a multiplication fact in the same fact family as 20 ÷ 5 = 4? (5 × 4 = 20 or 4 × 5 = 20)
- Why might this fact family be more confusing when we are multiplying or dividing by multiples of ten? (Possible response: Because 20 already ends in a zero.)
When dividing using multiples of ten, some underlying math facts present special cases. Those facts in which the product ends in zero (e.g., 5 × 2, 5 × 4) and where the dividend already has a zero in it (e.g., 20 ÷ 4, 30 ÷ 6) may be confusing to students, especially as they are trying to identify patterns and formulate rules.
Students' rules for subtracting zeros in division may not work since, as in this example, the quotient 20 ÷ 5 = 4 “loses” a zero in the process of dividing. For example, if a student's rule states that the number of zeros in the answer is equal to the number of zeros in the first number minus the number of zeros in the second number, the rule would not hold for a problem such as 200 ÷ 5. In this case, the rule would produce an incorrect answer of 400. Remind students that they should always keep the underlying math fact in mind when trying to apply a rule.
Practice Dividing by Multiples of Ten. Students complete Questions 1–7. Questions 1 and 2 provide more practice with numerical problems. In Question 3, students explain how they solved the problem for Question 2C. The explanation should include rules students developed for solving division problems with multiples of ten.
Check-In: Questions 4–7 are word problems involving division with multiples of ten. Students write division sentences to represent the situation as a division problem.
Use Check-In: Questions 4–7 in the Student Guide to document students' progress toward dividing numbers that are multiples of ten [E6].
Targeted practice for Expectation 6 is provided in the Lesson 5 Workshop.
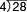 or 28/4 .
or 28/4 .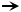 6 × ? = 54
6 × ? = 54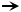 6 × ? = 540
6 × ? = 540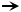 6 × ? = 5400
6 × ? = 5400