Paper-and-Pencil Division

Est. Class Sessions: 2–3

Developing the Lesson

Part 3. Practicing the Partial Quotients Method

The Paper-and-Pencil Division pages in the Student Guide provide additional explanation and practice. Have students read and discuss the two examples in pairs. Each partner can explain one example to the other. The first example has a whole number quotient. The second has a remainder. Ask questions to check that students understand what the numbers mean in each step.

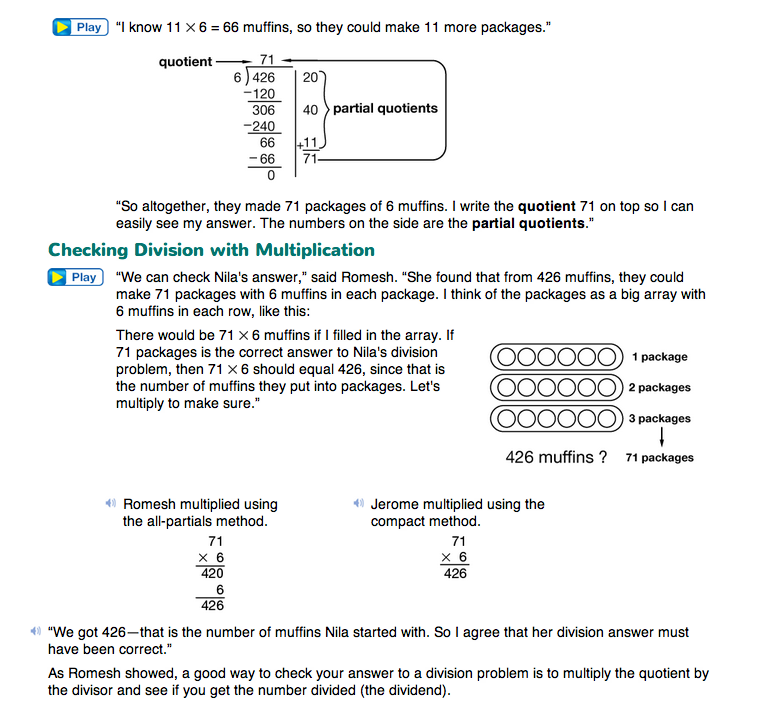
Have students complete Question 1 in groups. Ask them to explain the remainders. In Question 2, students check their answers using multiplication.

Question 3 presents four solutions to the same division problem. By now, students will have noticed that for each problem, there are several ways to choose partial quotients but they all result in the same answer. This makes the method very flexible and allows students to choose numbers they are comfortable working with. However, some choices are more efficient than others. When students are ready, they can start to look for choices that solve the problem in fewer steps.

Ask:

What is the first estimate in each solution in Question 3? (20, 30, 50, and 70)
Which one would you have tried first? Why? (Possible responses include: I would pick 20 because 20 × 5 = 100 is easy when you think of money; or I picked 70 because I tried to think of the biggest math fact that would help me. I skip counted by 5s until I got to 35, then I thought of 5 × 70 = 350.)
How do the estimates affect the next steps in the solutions? (If you can think of larger estimates, you can do the division in fewer steps.)

In general, when students choose partial quotients as large as possible (without going over), they will solve the problem in the fewest number of steps. In this case, the fourth solution has the same number of steps as the traditional long division method.

Have students complete Questions 4–5 still working in small groups or pairs. Have them compare their solutions and note the number of steps used.

When students have completed Questions 1–5 in groups or pairs, have them work independently to answer Check-In: Questions 6–9. As they work, circulate and observe which students are ready to use their math facts to look for larger first estimates to solve the problem in fewer steps and those who are not. Encourage, but do not require, students to solve the problem using the fewest steps. Particularly for those students who are progressing a bit more slowly, provide help so that they choose numbers that are comfortable for them, even if it takes more steps.

Use students' responses to Check-In: Questions 6–9 to assess their progress showing connections between models and strategies for multidigit division [E2]; interpreting remainders from division of multidigit numbers [E4]; and dividing multidigit numbers by 1-digit divisors using paper and pencil [E7].