Explore Multiplication by Multidigit Numbers
Est. Class Sessions: 2–3Developing the Lesson
Part 1. Multiplication Using Mental Math and Invented Strategies
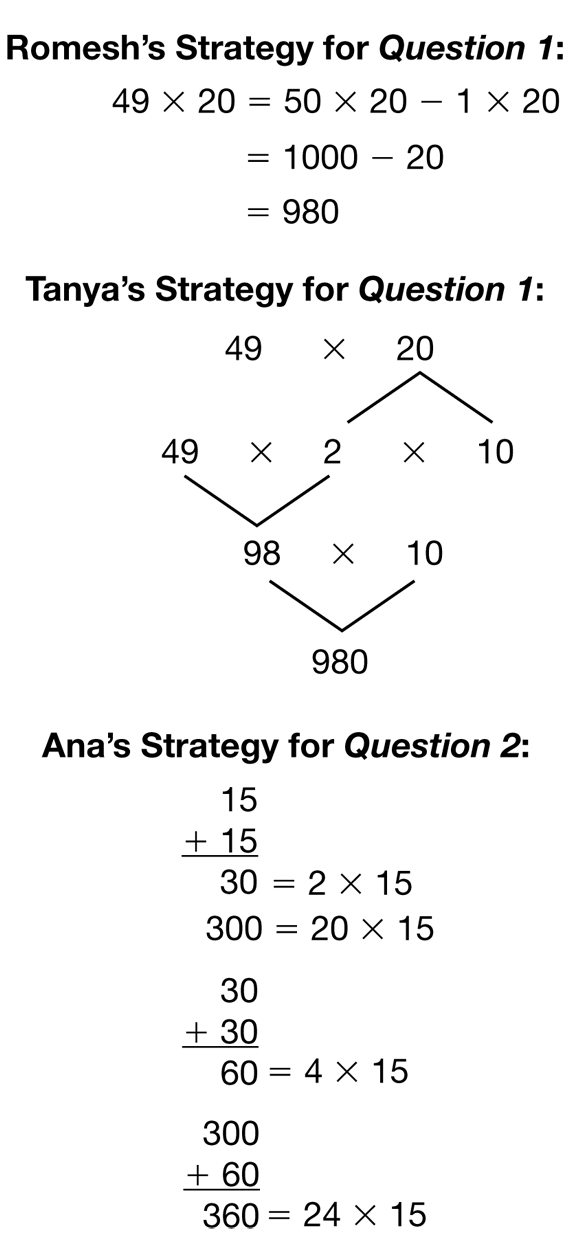
Ask students to read the opening vignette on the Explore Multiplication by Multidigit Numbers pages in the Student Guide. Ask students to work in pairs to solve the problems in Questions 1–2. Encourage students to solve the problems by breaking the numbers into parts or using simpler numbers. Ask volunteers to record their strategies on the board or chart paper and to explain them to the class.
As students explain their solutions, ask:
See Figure 1 and the Sample Dialog 1 for possible solutions to these problems.
If, after several strategies have been shared, a strategy similar to Romesh's does not come up, ask:
Once different strategies have been recorded, ask students to compare their strategies.
Ask: