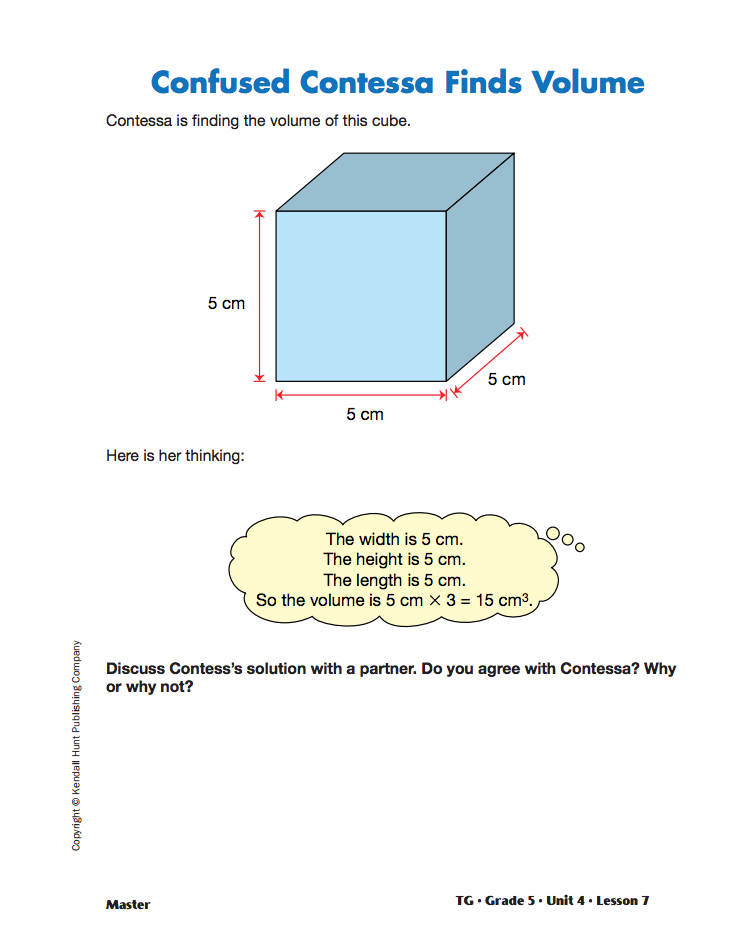
Check for Reasonableness. Display the Confused Contessa Finds Volume Master. Explain Contessa's work and ask student pairs to discuss it. Have centimeter connecting cubes available for student use.
- What do you think about Contessa's solution?
- Can you simply multiply one of the values times 3 as Contessa does? Is that reasonable? Why or why not? (No; Possible response: That would be 5 × 3 = 15 and that does not make sense. A cube with a width of 5 cm would have 5 layers each containing 25 cubes. A volume of 15 cm3 is much too small.)
- Show or tell how to correctly find the volume of the cube. (Possible response: Each layer has 5 rows of 5 cubes, or 25 cubes. There are 5 layers or 25 + 25 + 25 + 25 + 25. The cube would have a volume of 125 cm.)
- Who would like to show a different way to find the volume? (Possible response: 5 cm × 5 cm × 5 cm = 125 cm3.)
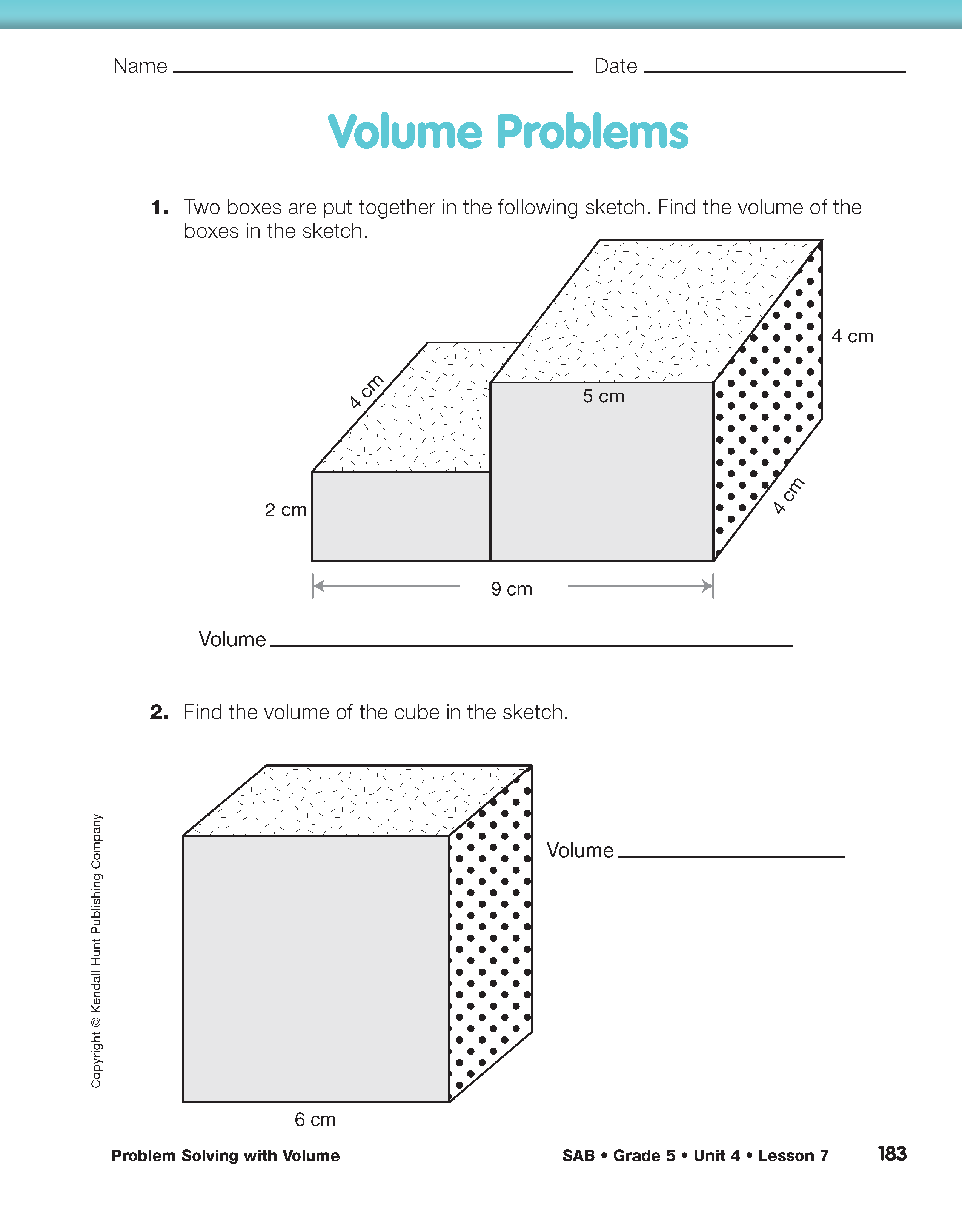
Use Multiplication and Division to Find Volume. Direct students' attention to the Volume Problems pages in the Student Activity Book.
- What is the difference between a box and a cube? (A cube's sides are all the same length. The sides of a box do not have to be all the same length.)
- How do you find the volume of a box? (Possible response: I could multiply the length times the width times the height of the box.)
- How do you find the volume of a cube? (A cube's sides are all the same length, so I can just multiply the length by itself 3 times.)
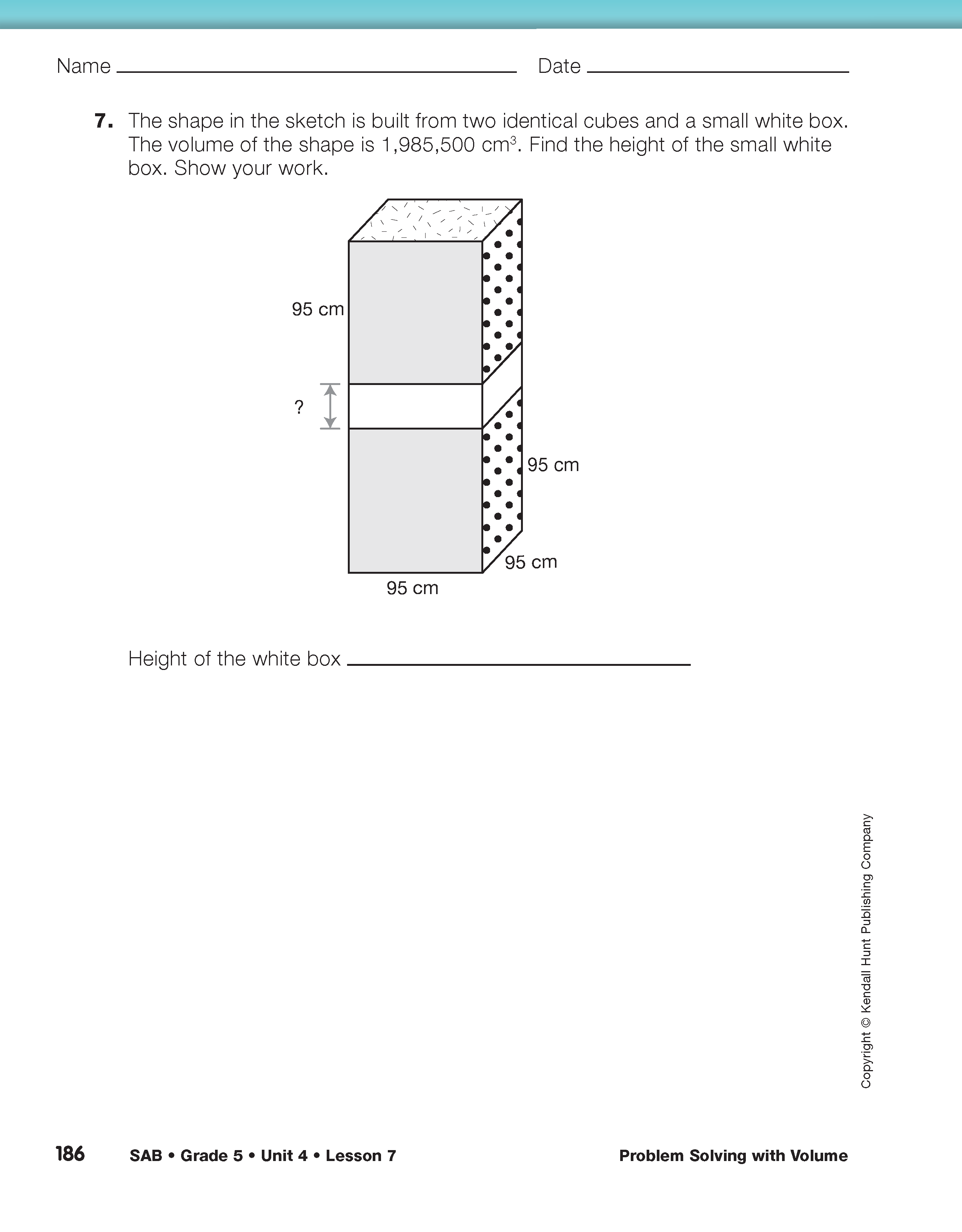
Assign Questions 1–7 to students or to student pairs. Students use multiplication and division strategies to find the volumes of boxes and cubes. Provide access to calculators. Question 6 shows a shape built from a box and a cube. The dimensions of the cube are provided, as is the total volume of the shape. Students need to find the unknown height of part of the shape. The problem provides scaffolding questions and steps to help students solve the multistep problem. There is a similar problem in Question 7; however, the question does not provide scaffolding.
Upon completion, display Question 7 of the Volume Problems pages in the Student Activity Book and discuss the strategies students used to solve the problem. See Figure 2. First, solve the problem together.
- What is the question to answer? (What is the height of the small white box?)
- What information is important in the problem? (Possible responses: The cubes are identical; the volume of the whole shape; each side of the cubes is 95 cm.)
- By just looking at the sketch, do you know the volume of the white box? (No, just that it is less than 95 cm × 95 cm × 95 cm because it is smaller than the cubes.)
- What do you know about the small white box? (Possible responses: I know that its length is 95 cm and its width is 95 cm; its height is less than 95 cm.)
- How does finding the volume of the small white box help you find its height? (Possible response: I know 2 dimensions of the small white box, the length and width. If I can find the volume, then I can find the height. I can multiply the length times width and then divide the volume by this number.)
- How does finding the volume of the two cubes together help you find the volume of the small white box? (Since I know the volume of the whole shape, I can subtract the volume of 2 cubes and find the volume of the box.)
- What is true about both cubes? (The cubes have the same dimensions and the same volume.)
- How do you find the volume of the two cubes together? (Possible response: One cube's volume is 95 cm × 95 cm × 95 cm = 857,375 cm3. The cubes are identical so the volume of both cubes is 857,375 cm3 × 2 = 1,714,750 cm3.)
- How do you find the volume of the small white box? (1,985,500 cm3 − 1,714,750 cm3 = 270,750 cm3)
- Now you know the volume of the small white box and its length and width. Show how to find its height. What do you do first? (Possible response:
The small white box's length times its width; 95 cm × 95 cm = 9025 cm2)
- What is the next step in finding the height? (Possible response: The small white box's volume divided by 9025; the height is 270,750 cm3 + 9025 cm2 = 30 cm.)
- Who would like to show the steps they took to solve the problem? What was your first step in solving the problem? Why?
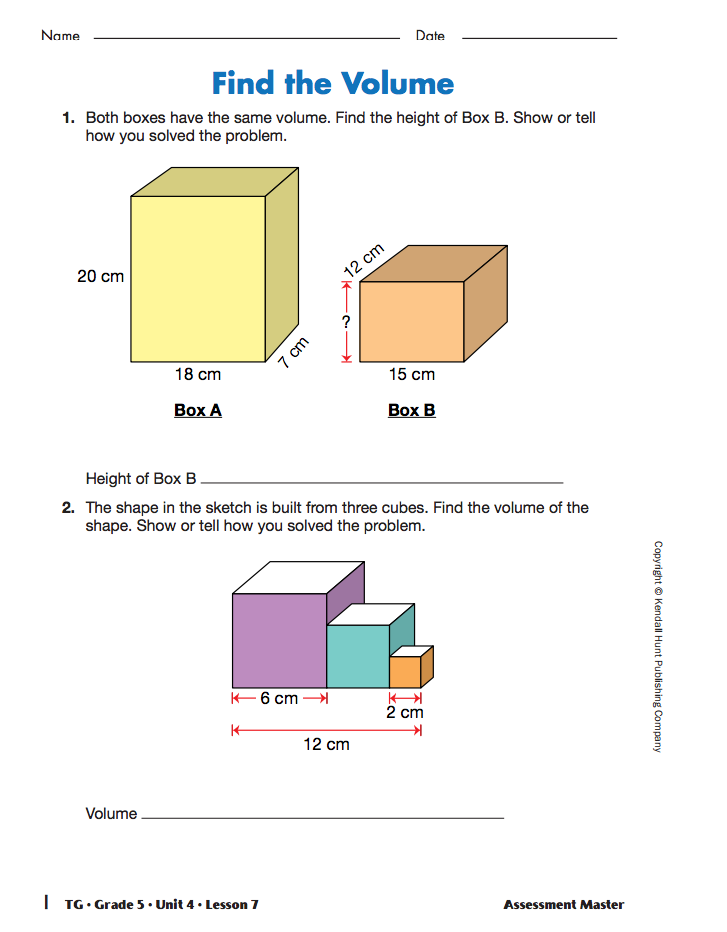
Display and direct students to the Math Practices page in the Student Guide Reference section. Students will focus on Math Practices 1, 2, 5, and 6 as they complete the Find the Volume Assessment Master individually.