Problem Solving with Volume

Est. Class Sessions: 2–3

Developing the Lesson

Part 1. Use Strategies to Find Volume

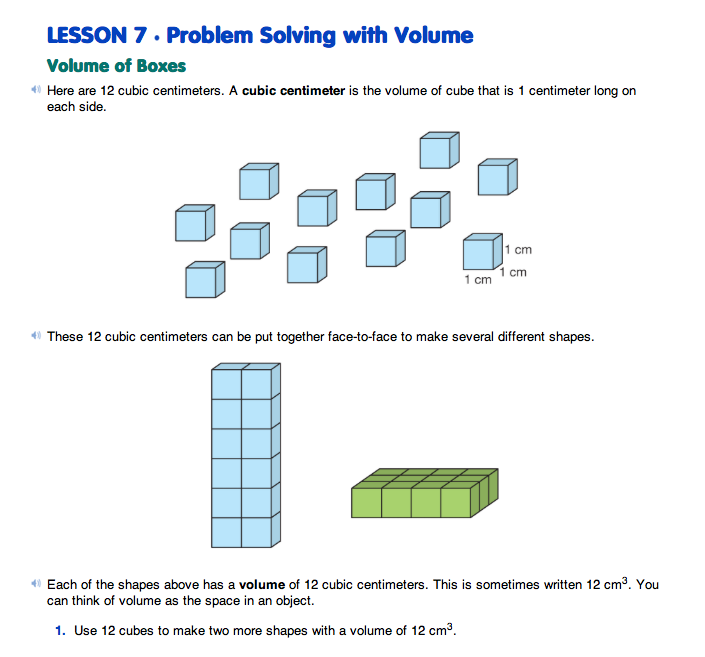
Find Volume of Boxes. Begin the lesson by directing students to the Problem Solving with Volume pages in the Student Guide. Ask students to read the definitions of a cubic centimeter and volume on the first page. Students learn that volume is the amount of space in an object and that it is measured in cubic units. A cubic centimeter is the volume of a cube that is one centimeter long on each side. Cubic centimeter can also be written as cm³.

Distribute a handful of centimeter connecting cubes to each student. Each student will need at least 24 cubes. In Question 1, students use the cubes to build two shapes with volumes of 12 cm³.

When students have each made two shapes, ask:

Compare your two shapes. What do you notice? (Possible response: The volume is the same.)
Does changing the shape affect the volume? Explain why you think so. (No, because the amount of space in the shapes does not change. I changed the shape, but I still used 12 cubes so the volume is 12 cm³ for each shape.)

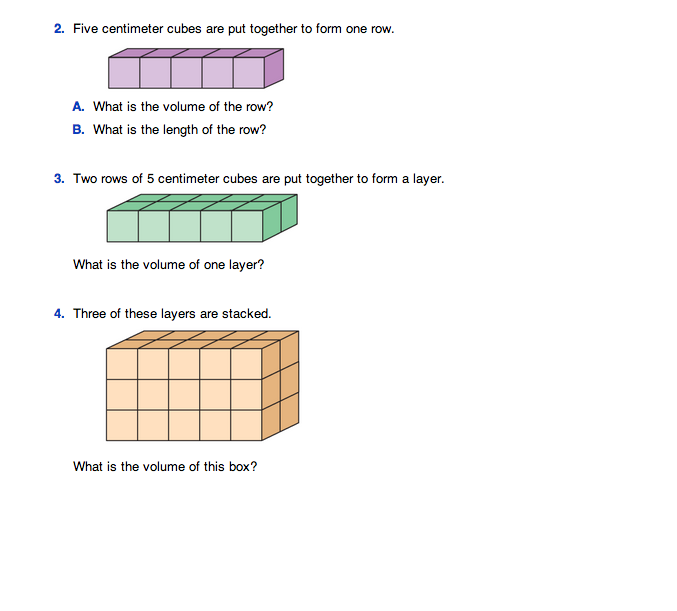
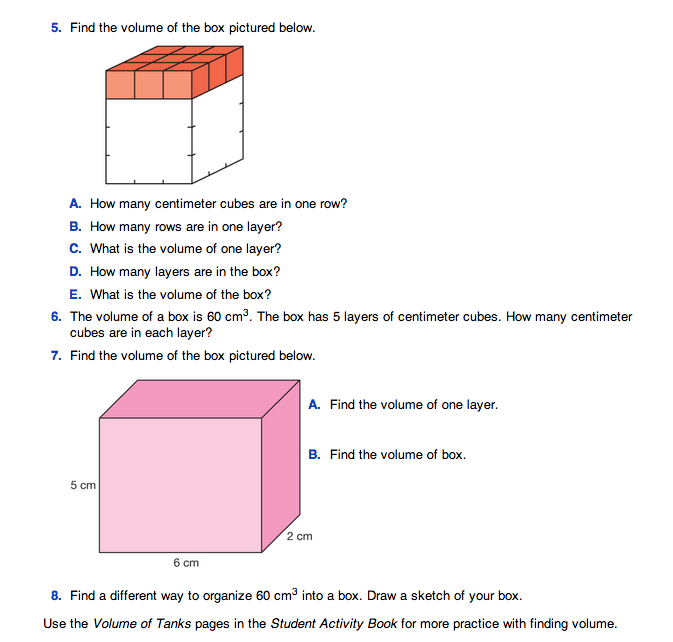
Assign Questions 2–8 to student pairs. Students answer questions about the volume of rows, layers, and boxes made of centimeter connecting cubes. Have centimeter connecting cubes available.

Upon completion, display Questions 5–7 of the Problem Solving with Volume pages.

Use prompts such as the following to discuss the strategies used to solve the volume problems:

Show or tell us how you found the volume of the box in Question 5. (Possible response: I knew the volume of one layer had 9 cubic centimeters. I counted 4 layers. 4 layers of 9 cubes is 36 cubes so the volume of the box is 36 cubic centimeters.)
When you knew the volume and the number of layers in the box in Question 6, how did you find the number of cubes in each layer? (Possible response: I thought about how many cubes had to be in 5 layers to make 60 or 60 ÷ 5 = 12. 5 layers of 12 cubes in each layer equals 60 cubes.)
How did you find the volume of the box in Question 7? How did knowing the volume of one layer help? (Possible response: I thought about rectangles. One side of the rectangular face on the bottom is 6 cm and another side is 2 cm. 6 × 2 = 12, so each layer has a volume of 12 cm³. There are 5 layers, so 5 × 12 = 60 cm³.)

Find Volume of Tanks. Tanks are slightly different from boxes in that they do not have a top. Display and direct students to the first Volume of Tanks page in the Student Activity Book. Use a copy of the Make a Tank Master and the step-by-step instructions in Question 1 to demonstrate how to construct a tank as students follow along. In Question 2, students find the volume of a 2 cm × 11 cm × 11 cm tank model.

Next, organize students into groups of four. Distribute 7 copies of the Make a Tank Master to each group. Assign Questions 3–5. Students will work with their groups to make other tanks from a 15 cm × 15 cm grid and find their volumes. Students may want to use tape on some of the taller tanks. Use a display of the table in Question 3 to discuss students' responses to Questions 4–5.

Ask:

What did you draw for Question 5?
Can you make a tank with a height of 8 cm from a 15 cm x 15 cm grid?
Why not? (Possible response: There isn't enough paper. The largest box would have a height of 7.5 cm and then the box would not have a volume because the base would be zero.)

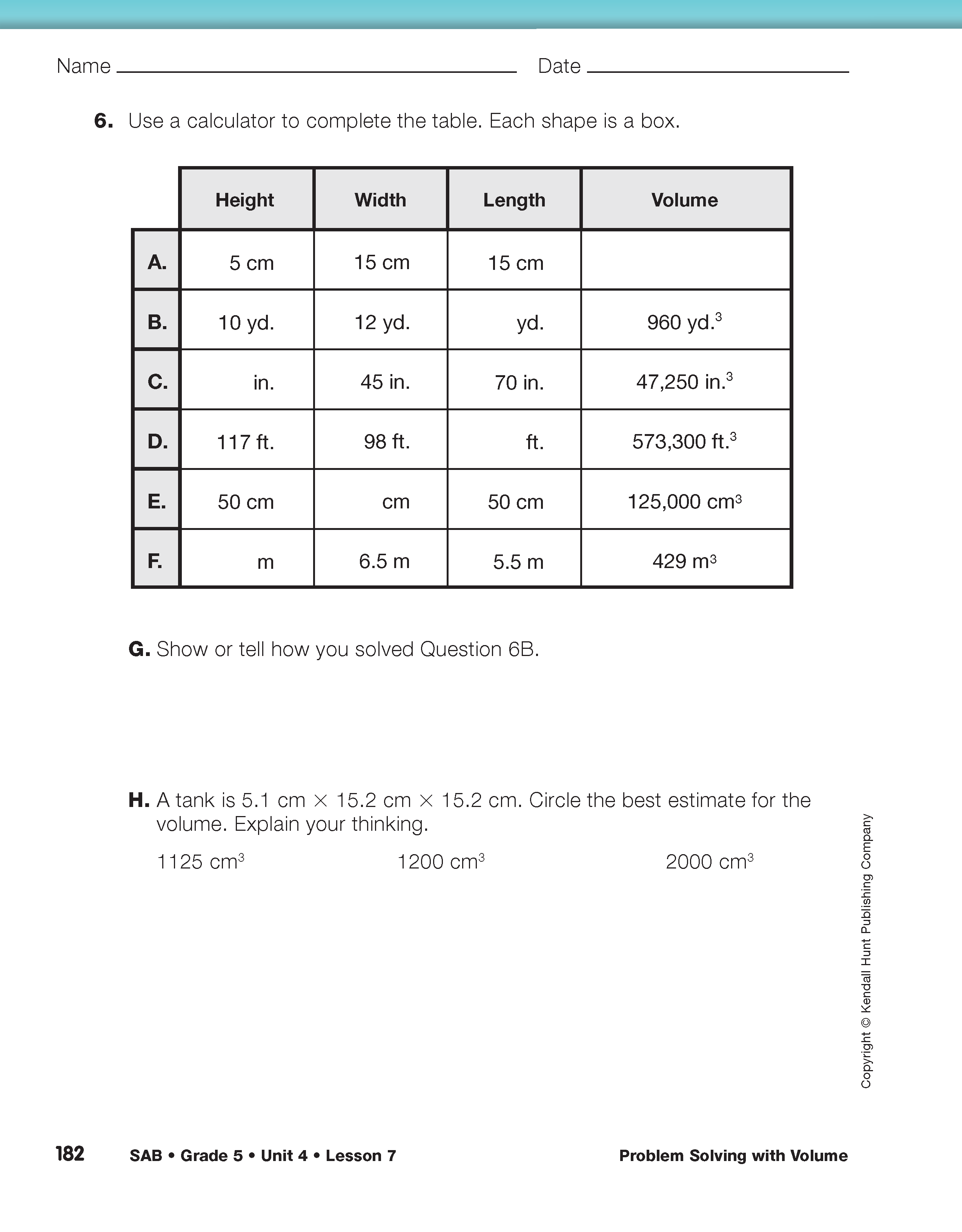
In Question 6, students will use multiplication and division strategies to find the missing values (height, width, length, or volume) in a table. Encourage students to use a calculator so that the goal of solving multistep problems is emphasized rather than the computation.

Upon completion, choose some of the problems in Question 6 to discuss. Have students explain how they found the missing values. If students know the length, width, and height, they can multiply these dimensions' values to determine the volume. Remind students of the inverse property between multiplication and division. If they know the volume and 2 of the 3 dimensions' values (height, width, length) they can first multiply the 2 values together. Next, they can divide the volume by this product to find the missing dimension. See Figure 1 for a sample solution to Question 6D. For some questions, students will label their answers with units of length (cm, yd., in., ft., m) but when finding volume, they will use cubic units.

Ask:

How did you label your answer?
When do you use cubic units? Why? (I use cubic units when I measure volume because I am multiplying the length times the width times the height and I am also multiplying the unit three times.)

Ask students to look at the table in Question 6.

Ask:

What information is missing this table? (Sometimes the volume is missing and sometimes one of the other dimensions is missing.)

Ask students to work with a partner on the problems in Question 6.

As students are working circulate and ask:

How did you find the [length] of that shape?
[50 cm] × [50 cm] × [what] gives you [125,500]?
How did you find the missing number?

Gather students to share their strategies to Question 6B and discuss the problem described in Question 6H.

Ask:

Look at the boxes in the table. Which box is this box similar to? (the box in Question A)
Did you lengths of the sides get smaller or larger? (The lengths are larger.)
What do you think will happen to the volume? (Possible response: The volume will get larger.)
Which estimate do you think is the most reasonable? (Possible response: 1200 cm³.)
Why? (Possible response: 1125 is the volume of the box in Question A so this box has to have a larger volume and 2000 cm³ just seems too large. Each length just got a little bit larger.)