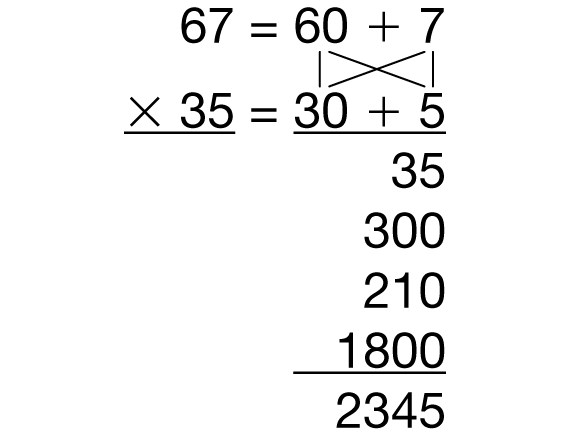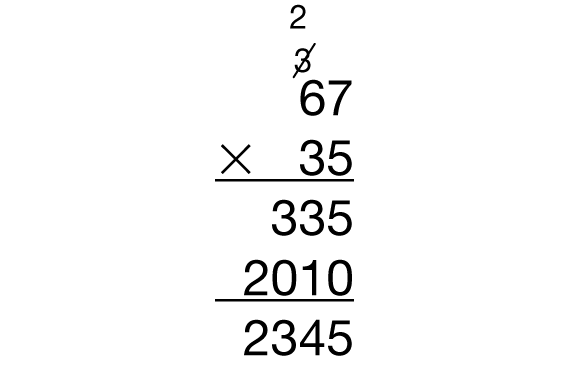Workshop: Multiplication Strategies

Est. Class Sessions: 3

Developing the Lesson

Part 1. Practice Multiplication Strategies

Solve Multiplication Digits Game Problems. Begin the lesson by reading the first paragraph on the Workshop: Multiplication Strategies pages in the Student Guide. Ask students to just look at the game boards and estimate the products in order to predict who won the game.

Ask:

How did you estimate the products? Who do you predict will win? (Possible response: I estimated by using round numbers. I multiplied 70 × 90 = 6300 for Tanya and 90 × 60 = 5400 for Jerome, so I predict Tanya will win.)

Next, ask students to answer Question 1. They will use the all-partials method to find Tanya's product. See Figure 1. Students should refer to the Multidigit Multiplication Strategies Menu in the Student Guide Reference section and refrain from using calculators.

Ask:

Explain the steps you took when using all partials to solve Tanya's problem. (See Figure 1 for an example.)
Where did the partial product [320] come from? (80 × 4 = 320)
Why did you write [5600]? (Possible response: 8 tens times 7 tens is 56 hundreds or 5600. 8 × 7 = 56 and 10 × 10 = 100. 56 × 100 = 5600.)
Who would like to show another way to solve this problem so that we can check for reasonableness? Did anyone use expanded form, a rectangle model? (See Figure 2 for an example.)

Have students complete Question 2. They will use the compact method to find Jerome's product. As students work, ask them to demonstrate how the compact method works by explaining how the carried numbers connect to place value.

Upon completion, ask:

Show us how you used the compact method to solve this problem. (See Figure 1.)
When you multiplied 4 ones times 7 ones, why did you write the 2 above the tens column? (4 × 7 = 28. I wrote a 2 above the tens column to remind myself that I had to add 2 tens on to the product of 80 × 4.)
Did you do this at any other time when solving this problem? Explain. (When I multiplied 60 × 7, I got 420. I put a 4 above the tens column to remind me to add 400 to 60 × 80.)
Who would like to show another way to solve this problem so that we can check for reasonableness? (See Figure 2 for an example.)
Do you prefer all-partials, the compact method, or a different way for solving these problems? Why?
Which student won the game [Question 3]? (Tanya)
How would the strategy change if the goal were to get the smallest product? (Possible response: In Tanya and Jerome's game, they probably tried to put the largest digits in the tens place. If the goal were to get the smallest product, I would put the smallest numbers possible in the tens places.)

Tell students they will have an opportunity to play the Multiplication Digits Game after they have had time to practice a variety of multiplication strategies. Students who finish their work may play the game, and then time will be devoted again at the end of the Workshop for all to play. If needed, briefly review the directions of the game using a display of the Multiplication Digits Game Master. Student groups will need a set of 0–9 Digit Cards, paper, and pencils.

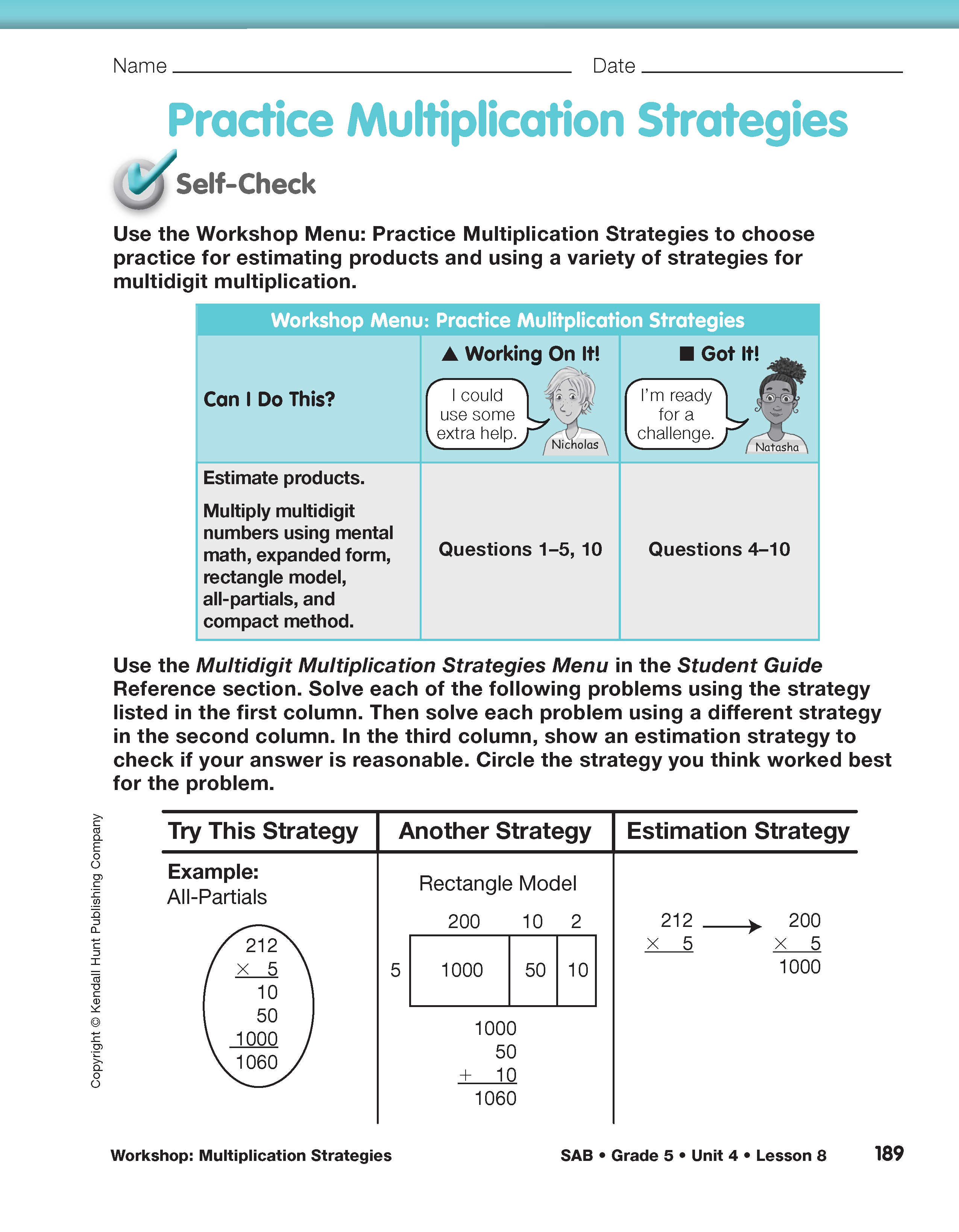
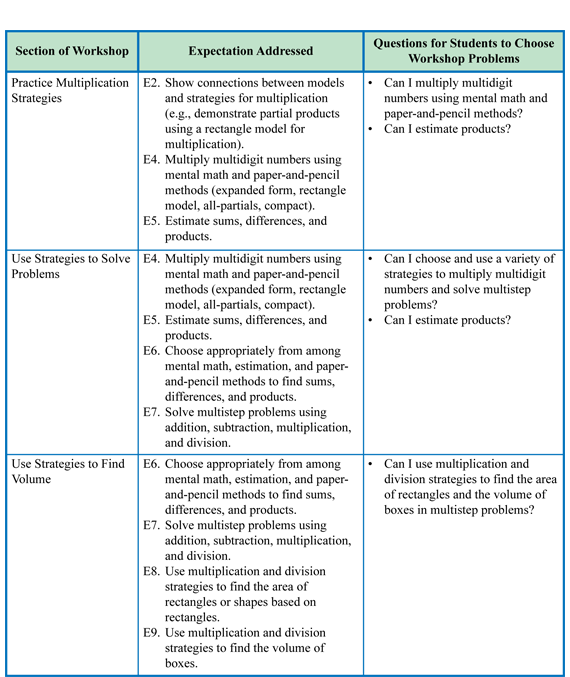
Choose Targeted Practice. Menus and problems for this Workshop are in the Student Activity Book on the Practice Multiplication Strategies pages and in the Student Guide on the Workshop: Multiplication Strategies pages. Minis of these pages not shown here are in the Answer Key. This Workshop is divided into three sections that address Expectations as shown in Figure 3.

Direct students to the Practice Multiplication Strategies pages in the Student Activity Book. Students begin each section of the Workshop with a Self-Check. For this first section, students self-assess by simply thinking about the “Can I Do This?” questions in the left-hand column of the menu. In other sections of the Workshop, students will complete a Self-Check Question. These questions serve two purposes. First, they clearly communicate the content of the related targeted practice to students. Second, they help students quickly self-assess their progress with Expectations to help them choose which problems to work on in the Workshop. Ask students to think about their progress with these Expectations and choose from the following groups:

Students who are “working on it” and need some extra help should circle the problem set marked with a triangle (). These problems provide scaffold support for developing the essential underlying concepts as well as some opportunities for practice.
Students who are “getting it” and just need more practice should circle the problem set marked with a circle (). These problems provide opportunities to practice with some concept reinforcement and some opportunities for extension.
Students who have “got it” and are ready for a challenge or extension should circle problems marked with a square (). These problems provide some practice and then move into opportunities for extension.

Students use the Self-Check Workshop Menu: Practice Multiplication Strategies on the Practice Multiplication Strategies pages in the Student Activity Book to assess their abilities and choose appropriate practice estimating products [E5] and multiplying multidigit numbers using paper-and-pencil methods (expanded form, rectangle model, all-partials, compact) [E4].

Check students' choices to see how well they match your own assessment of their progress on the related Expectations. Help students make selections that will provide the kind of practice they need.

Once students select the questions to complete in a section of the Workshop, have students work independently or with a partner to solve the problems they chose. Match groups of students who have chosen similar sets of problems from the menu. Encourage students to use the Multidigit Multiplication Strategies Menu in the Student Guide Reference section as they are working.

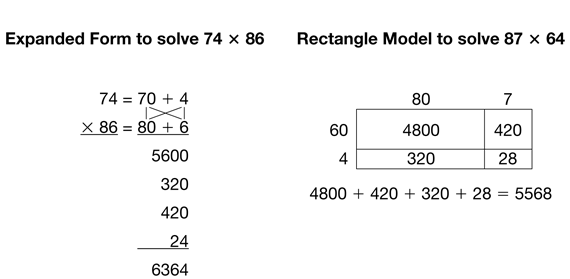
The problems on the Practice Multiplication Strategies pages provide practice using a variety of multiplication strategies: mental math, rectangle model, all-partials, expanded form, and the compact method, as well as estimation strategies.

Challenge students who are more confident with one or two methods to try others from the Multidigit Multiplication Strategies Menu and to use as many different ones as they can. Ask them to choose efficient methods based on the numbers in the problem.
If students using the compact method have difficulty explaining how the carried numbers connect to place value, ask them to use expanded form to partition the numbers and make connections between the expanded form and compact method.
For students who have difficulty using the compact method, encourage them to use a rectangle model, expanded form, or the all-partials method.

Upon completion, display and discuss Check-In: Question 10 which involves multiplying a 2-digit number by another 2-digit number.

Ask:

How did you estimate the product? (Possible response: 70 × 30 = 2100)
How did Tanya get the partial product 1800? (She multiplied 30 × 60.)
What part of Jerome's rectangle matches with this partial product? (The largest part of the rectangle, 30 × 60.)
Who would like to show how to use expanded form to solve 67 × 35? (See Figure 4.)
Who would like to show how to use the compact method to solve 67 × 35? (See Figure 5.)
Explain how you used your estimate to check the reasonableness of your product. (Possible response: My estimate was not even close to my answer so I used a different method to multiply. I got an answer that was closer to my estimate, so I decided that was a more reasonable answer.)

Use Check-In: Question 10 and the Feedback Box on the Practice Multiplication Strategies pages in the Student Activity Book to assess students' abilities to estimate products [E5]; show connections between models and strategies for multiplication [E2]; multiply multidigit numbers using paper-and-pencil methods (expanded form, rectangle model, all-partials, compact) [E4]; check for reasonableness [MPE3]; and show work [MPE5].