Paper-and-Pencil Multiplication

Est. Class Sessions: 2

Developing the Lesson

Play Multiplication Digits Game. This game follows the same basic rules as the Digits Game from Lesson 1 of this unit, but the game board is arranged as a multiplication problem instead of an addition problem.

Cards are drawn one at a time from a deck of digit cards. Students attempt to make the largest or smallest product by strategically placing the digits on a game board. Start by only playing for the largest product and vary it once students have had more practice.

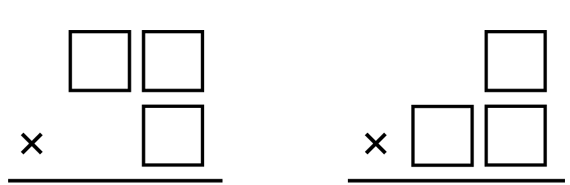
Model playing the game with the whole class. To play the game, students draw boxes on their papers as a template for a multiplication problem. Begin with the game boards shown in Figure 1 to introduce the lesson. The game will be repeated at the end of the lesson with multiplication problems involving numbers with more digits.

Using the Digit Cards 0–9 from Lesson 1, the teacher or game leader draws cards one at a time. Students place numbers in the boxes as each is read. Once a digit is placed, it cannot be moved. When all the boxes are filled, students find the answer to the problem. Ask students to use a second method to check their answers or estimate to see whether they are reasonable. Then decide as a class which answer is the largest and who is the winner.

The directions for the game are in the Multiplication Digits Game section in the Student Guide. Encourage students to think carefully as they place digits in the boxes. To place numbers advantageously, students have to use their knowledge of place value and notions about probability. After a game is completed and students have found their answers, discuss their choices for placing numbers.

Using a game board that looks like the first one in Figure 1, ask:

If you are playing for the largest product and the first card drawn is a 9, where would you place it? (Possible response: The tens place in the top factor would be the best place, since this would have been true when I played the game with addition problems.)
Are there any other places that would make sense? (For multiplication, the ones place of the bottom factor would also ensure a large number.)
Does it make a difference whether you put it in the tens column of the first factor or in the ones column of the second factor? (Possible response: Placing it in the bottom factor will ensure a slightly larger number because both digits of the top factor are multiplied by the largest possible digit.)

A discussion of where students chose to place the 9 provides opportunities for them to communicate their knowledge of place value and multiplication. Play several games with the same game board. Tell students they will play the game again at the end of the lesson using the game boards with more digits.

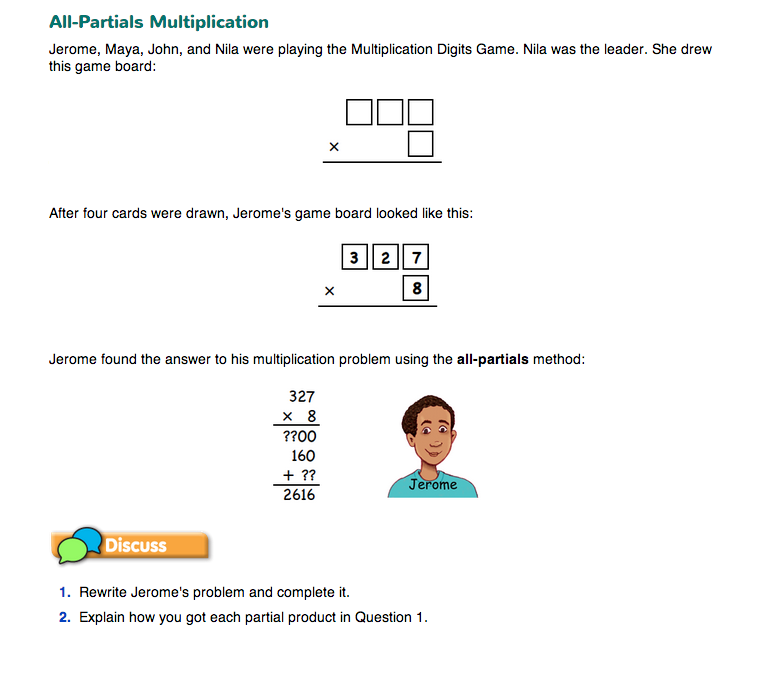
Use the All-Partials Method. Read the vignette in the All-Partials Multiplication section of the Student Guide.

Ask:

What is the difference between the game boards you used and the one Jerome is using? (The top factor now has a digit in the hundreds place.)

Use Questions 1–2 to explore the all-partials method for multiplication.

Ask:

How is Jerome's method similar to the expanded form method for multiplication? How is it different? (It is the same as the expanded-form method except that the expanded form of each number is not written out before multiplying each partial product.)
How is Jerome's method similar to the rectangle model? (Jerome multiplied 8 times the hundreds, tens, and ones in the top factor and got the same numbers you would put in the rectangles. Then all the products are added together.)
What did Jerome multiply together to get the 2400 on the first line? (300 × 8 or 8 × 300)

Students may respond by saying that he multiplied the 3 times the 8. In this case, ask them what the value of 3 × 8 is. Point out the important place-value difference between saying 300 × 8 and 3 × 8.

After discussing Jerome's strategy, have students complete Questions 3–4.

Once students have completed sketches of Maya's rectangle in Question 3, ask:

What the length of the largest rectangle? (800)
What is the length of the shortest? (7)
What is the value of the missing area? (7 × 800 = 5600)

Use Question 4 to reconnect to the Multiplication Digits Game. Students determine the greater product between Jerome's and Maya's boards.

Ask:

What would be a quick way to figure out who won the game? (Compute the largest partial product of the leading digits for each. 800 × 7 = 5600 is greater than 300 × 8 = 2400, so Maya should win the game.)
Will this method always work to determine a winner? (Yes, unless the leading partial products are the same for both players. Then the smaller partial products must be checked.)
Why does this checking method work? (The leading digits have the highest place value; so they have the greatest influence on the total product.)

Remind students that they can test their strategies for winning when they play the game again later in the lesson.

Assign Questions 5–8 to students. In these questions students explore the all-partials method for multiplying a two-digit number by a two-digit number. As students work, ask them to compare this method to the expanded form and rectangle methods.

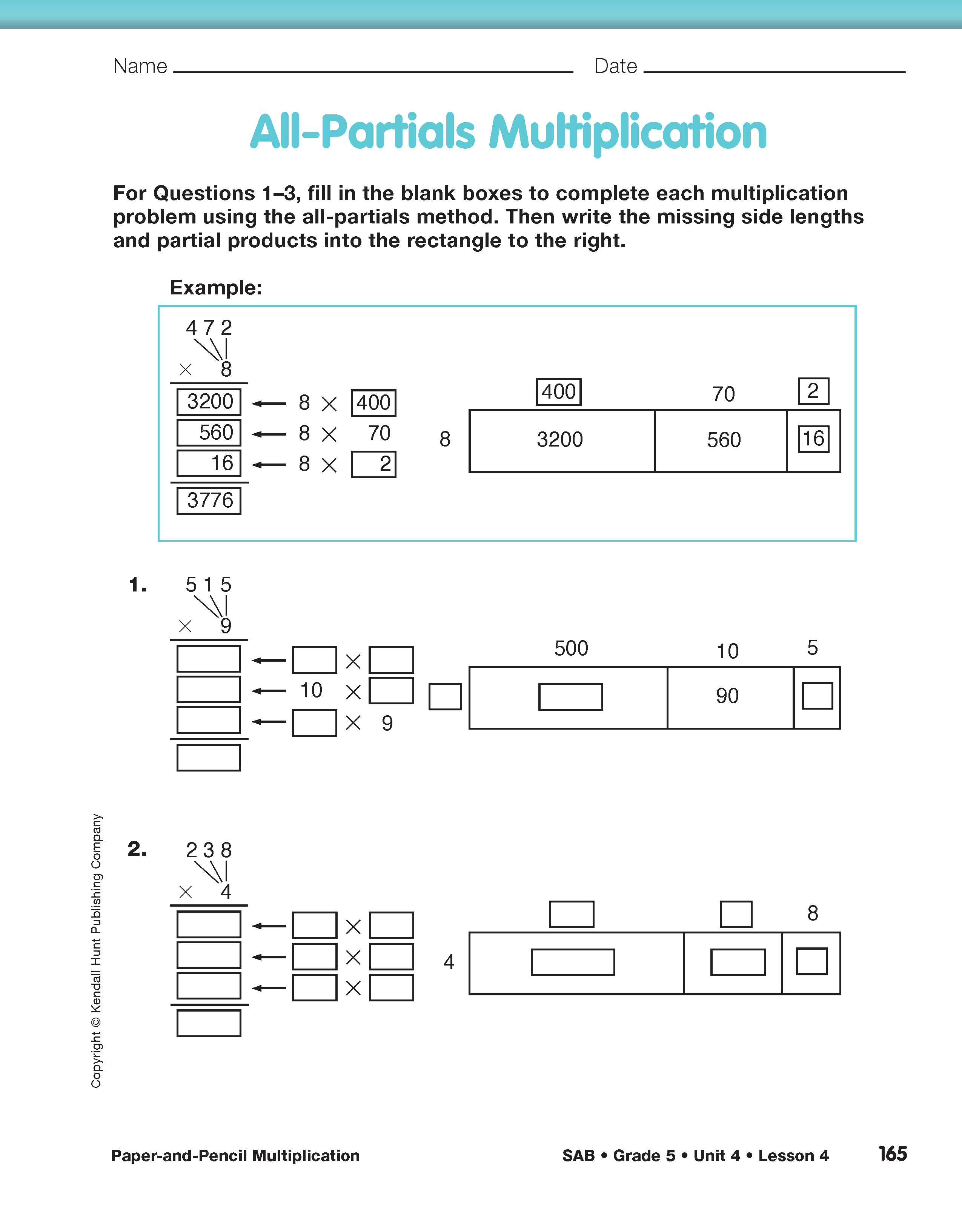
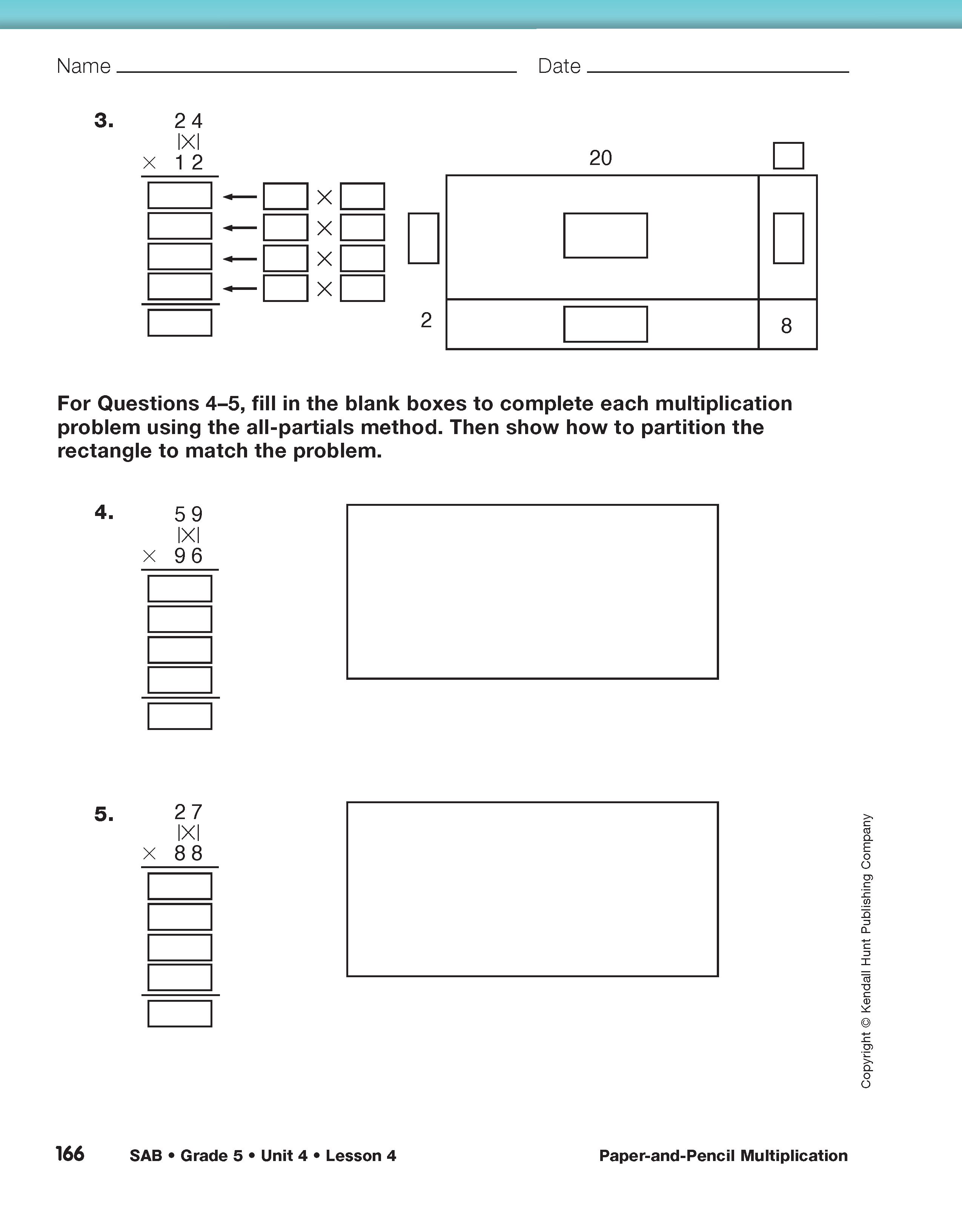
Direct students to the All-Partials Multiplication pages in the Student Activity Book. Ask students to complete Questions 1–5 to assess their abilities to use the all-partials method of multiplication.

Use the All-Partials Multiplication pages in the Student Activity Book to assess students' abilities to show connections between the all-partials method for multiplication and the rectangle model for multiplication [E2].

Use the Compact Method. Read the vignette about Marcie's Pet Store in the Compact Method for Multiplication section in the Student Guide.

Ask:

What multiplication problem are Jacob and Nicholas trying to solve? (315 × 5)
What are the partial products in Jacob's method (Question 9)? (5 × 5 = 25; 10 × 5 = 50; 300 × 5 = 1500)

Read through the explanation of Nicholas's compact method that follows Question 9 with the class.

Ask:

What differences do you notice between Jacob's and Nicholas's method (Question 10)? (Jacob's method shows all of the partial products, but Nicholas's method does not. Nicholas's method takes less space but is not as clear about where the answer comes from.)

In Question 11, students explain preferences for the all-partials method or the compact method.

Ask students to explain their reasoning for preferring one method over the other with questions such as:

Which method is easier for you to learn?
Which makes more sense to you? Why?
Which method helps you multiply more accurately?
Can either method help you estimate quickly?
Which method helps you multiply more quickly?

Use Question 12 to check students' understanding of the steps in the compact method. Question 13 provides practice with using the compact method to multiply by a single-digit number. Remind students to consistently use mental math and estimation strategies to check the reasonableness of their answers. Question 14 asks students to explain how they will do this for one of the problems.

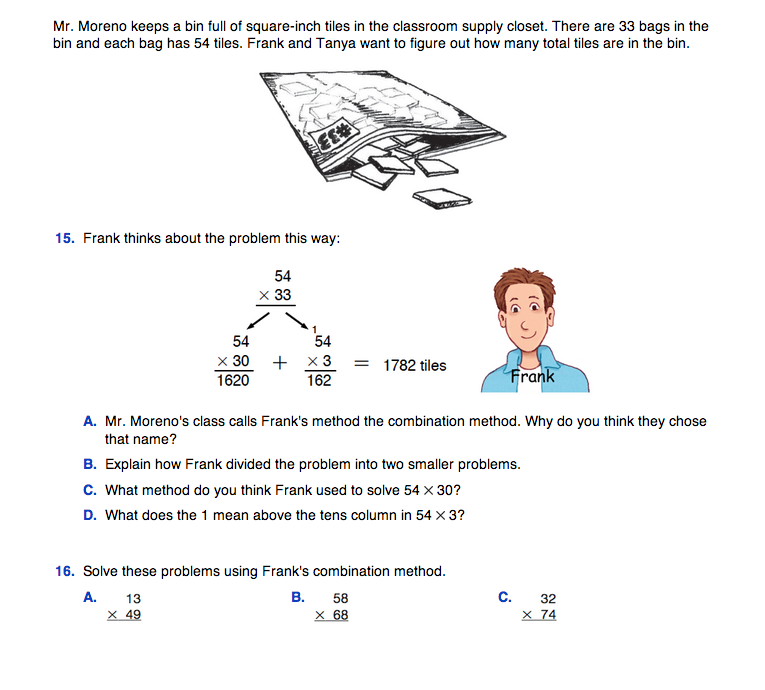
Use Questions 15–16 as an introduction to the compact method for multiplying multidigit numbers. These questions discuss the combination method, where two-digit by two-digit multiplication problems are broken into two simpler problems by partitioning one of the factors. Solving problems by this method leads directly into a discussion of the compact method for two-digit by two-digit multiplication.

Ask students to read the Tanya's Compact Method section of the Student Guide and then complete Questions 17–18. Question 18 leads students through a step-by-step explanation of each step Tanya used to solve 49 × 64.

Assign Check-In: Question 19. Students should complete these questions independently in order to check their understanding of multiplication strategies.

Use Check-In: Question 19 in the Student Guide to assess students' abilities to multiply multidigit numbers using mental math and paper-and-pencil methods (expanded form, rectangle model, all-partials, compact) [E4] and estimate sums, difference, and products [E5].