Area Problems

Est. Class Sessions: 2

Developing the Lesson

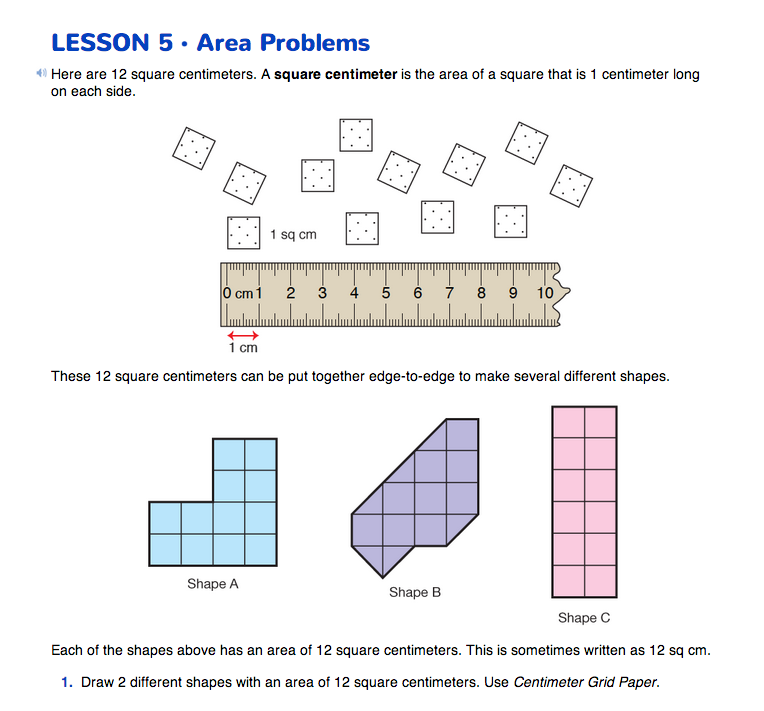
Find Area. Begin the lesson by directing students' attention to the Area Problems pages in the Student Guide. Read the introductory paragraphs together as a class. Students will learn that a square centimeter is the area of a square that is 1 centimeter long on each side. The area of each of the shapes on the page is the amount of space the shape covers, or 12 square centimeters.

Distribute one copy of the Centimeter Grid Paper Master to each student and assign Question 1. Students will use a ruler to draw two different shapes with an area of 12 square centimeters on the Centimeter Grid Paper.

To help students design a shape with an area of 12 square centimeters, provide students with 12 square inch tiles that they can manipulate. Students can then record their design on Centimeter Grid Paper.

Ask students to exchange their shapes with a partner. Instruct partners to verify that the shapes' areas are 12 square centimeters.

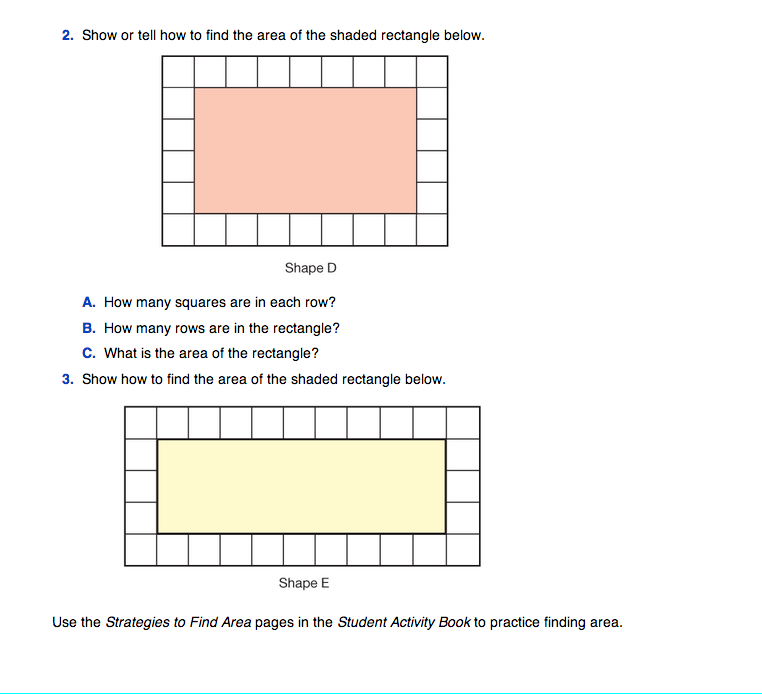
Assign Questions 2–3. Students will find the area of two rectangles. Students can find the area of Shape D in Question 2 by counting, but encourage a more sophisticated and efficient multiplication strategy. Note that there are 4 rows of 7 square centimeters each or 7 columns of 4 square centimeters each and that they can multiply or skip count to get 28 square centimeters. Students may also find half of the rectangle's area (2 × 7 = 14 sq cm) and then double it (14 + 14 = 28 sq cm). Similar strategies can be used to find the area of Shape E in Question 3.

Upon completion, discuss the various strategies students used to find the area of the rectangles, and compare the positive and negative aspects of each strategy. Generalize with students that the area of a rectangle is the length times the width. Remind students to use the correct units when sharing their answers.

There is no hard-and-fast rule for defining which side of a rectangle is the length and which is the width. The longest side is usually called the length, and an adjacent side the width, but this is not necessary.

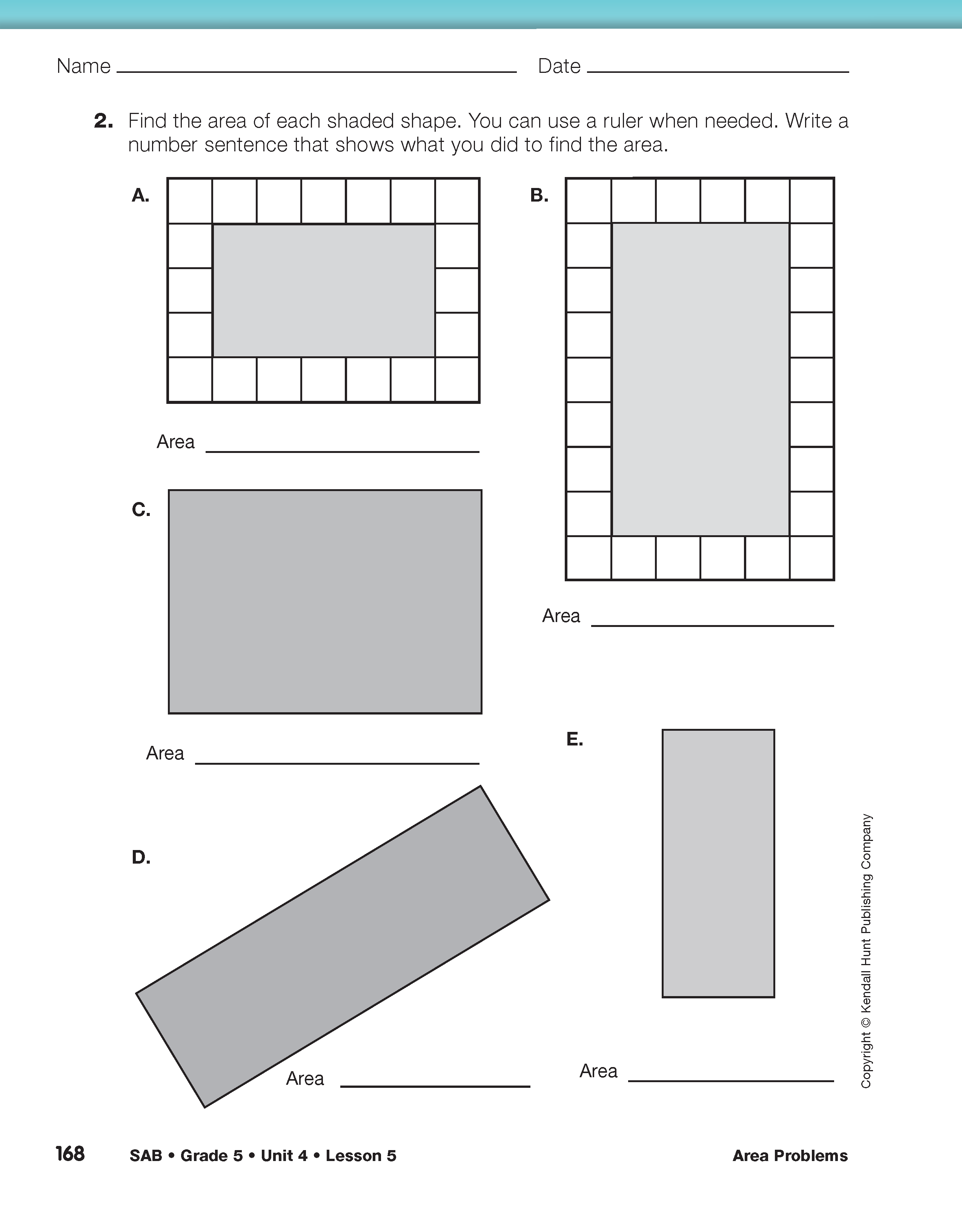
Use Strategies to Find Area. Use the Strategies to Find Area pages in the Student Activity Book to provide practice with finding area. Assign Questions 1–4 to student pairs. In many questions, rectangles are drawn on a grid that can help students find length and width, with the exception of Question 1C. Students may simply count the squares and half squares in this question. For Question 2C–E, students will need to measure dimensions with a ruler. Likely, students will use multiplication and partitioning strategies to find area.

After students have had time to work through the problems, display the Strategies to Find Area pages and discuss Questions 1C–D. Ask students to look at the shape in Question 1C closely. They should notice that the rectangle is not made entirely of whole centimeter squares and that it has twelve half-centimeter squares. Students must find a strategy to combine two half-squares to make one whole centimeter square in order to find the total area, 16 square centimeters.

Ask:

How did you find the area of the rectangle in Question 1C? (Possible response: Since there were whole squares and half squares, I just counted 10 whole centimeter squares and 12 half-squares. I put the half squares together to make 6 more whole squares. I got an area of 16 square centimeters.)

If they don't suggest it, have students simply count the squares in this rectangle first. Next, have students use a ruler to measure each side to the nearest tenth of a centimeter. They will find that while the shape is still a rectangle, the diagonals are not whole centimeters long. If they multiply length (5.7 cm) by width (2.8 cm) on their calculators, 5.7 cm times 2.8 cm equals 15.96 sq cm. The answer displayed on the calculator, while close to 16 sq cm, will not be the exact area of the rectangle. Remind students that since they are using the rulers to only measure to the nearest tenth of a centimeter, they cannot measure the length of a side exactly and cannot find the rectangles exact area by multiplying 5.7 cm × 2.8 cm. See Content Note.

When determining the area of the rectangle in Question 1C, students' calculations (15.96 sq cm) will not match the number of square centimeters they count (16 sq cm). Measuring the diagonals (the short sides of the rectangle) to the nearest tenth of a centimeter with rulers, students find they are 2.8 cm. However, because the side lengths of the rectangle are built on diagonals that are the hypotenuses of right triangles, the side lengths are not each exactly 2.8 cm. The short sides of the rectangle are each really 2.828427125 cm. The long sides of the rectangle are each really 5.656854249 cm. In this situation, counting the whole and half-square centimeters finds a more accurate area.

Ask:

How did you find the area of the shape in Question 1D? (See Figures 1 and 2 for possible responses.)

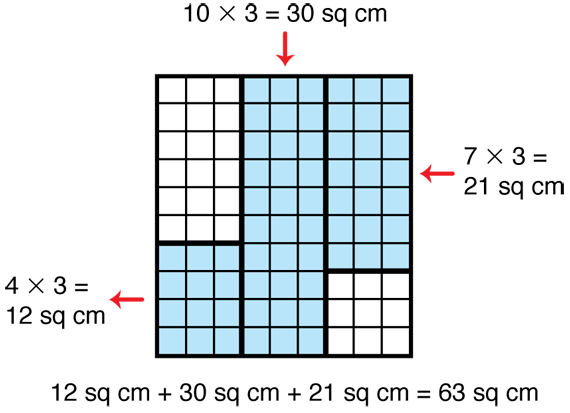
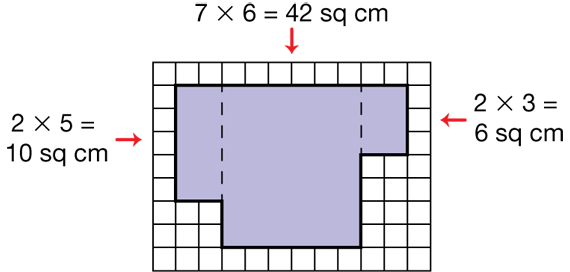
One possible strategy to find the area of the shape in Question 1D is to divide this large shape into several smaller rectangles as shown in Figure 1. Find the area of each smaller rectangle and then add the areas together to arrive at the total area of 63 sq cm.

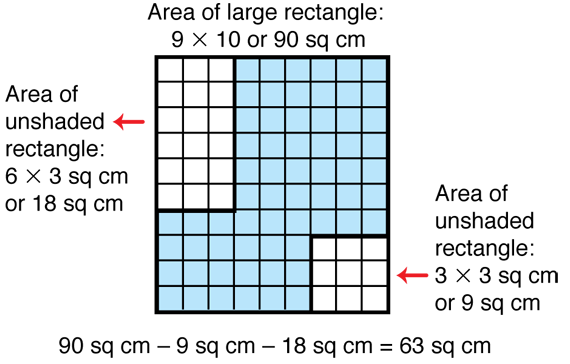
Another possible strategy is to draw the rectangle that surrounds this shape and find its area (90 sq cm) as shown in Figure 2. Find the area of the two unshaded rectangles (18 sq cm and 9 sq cm). Then subtract the total from 90 sq cm to find the area of the shaded shape.

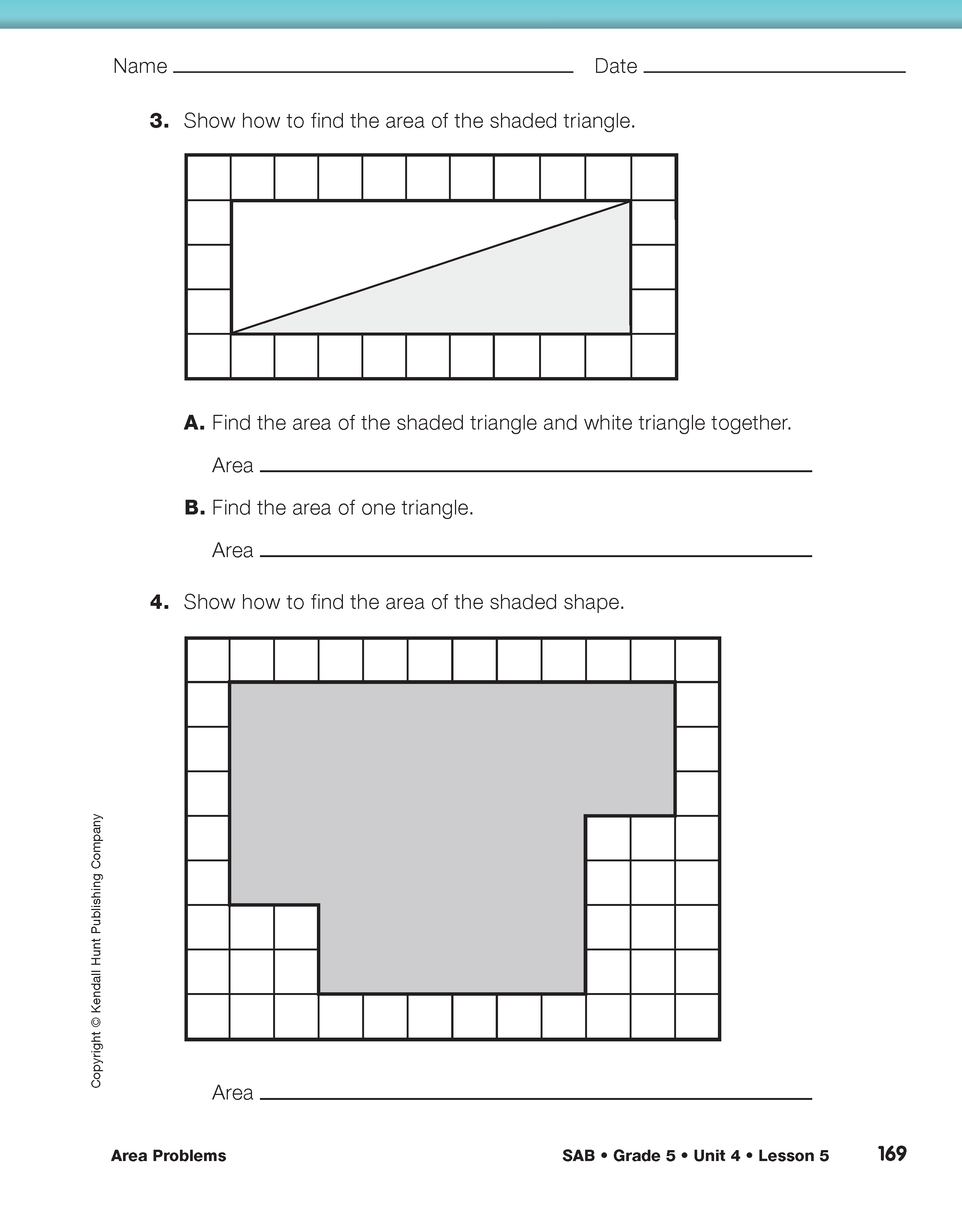
Discuss Questions 2E–4.

Ask:

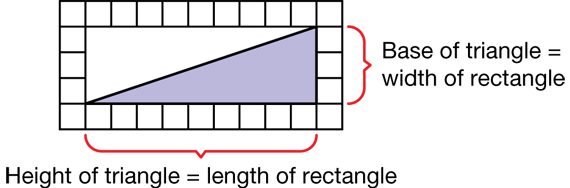
How did you find the area of the rectangle in Question 2E? (Possible response: I measured one short side of the rectangle and got 2.5 centimeters. I measured one long side of the rectangle and it was 6 centimeters. First, I just thought about the whole numbers and I multiplied 6 × 2 = 12. I know .5 is a half, so I added 6 halves to get 3 wholes. 12 + 3 = 15 square centimeters.)
Look at Question 3. What do you notice about the shaded triangle? (Its area is half the area of the rectangle.)

Students can fold a copy of the rectangle in Question 3 to find that the triangle is half the area of the rectangle. The height of the triangle is equal to the length of the rectangle and the base of the triangle is equal to the width of the rectangle. See Figure 3. The intention is not to develop the formula for the area of a triangle at this point but rather slowly build intuitive understanding. One possible strategy to find the area of a triangle is to draw a rectangle to surround the triangle and find its area. Divide this in half to find the area of the rectangle.

Ask:

How did you find the area of the shaded triangle and the white triangle together in Question 3? (Possible response: The two triangles together make a rectangle that is 3 sq cm by 9 sq cm, and 3 × 9 = 27 sq cm.)
How did you find the area of the one triangle? (Possible response: One triangle is exactly half of the 27 sq cm rectangle. 13.5 + 13.5 = 27 so the area of one triangle is 131/2 sq cm.)
Did anyone find the area of one triangle a different way?
How did you find the area of the shaded shape in Question 4? (Possible response: I divided the shape into 3 rectangles. [See Figure 4.] I had a 2 × 3, a 7 × 6, and a 2 × 5 rectangle. The area of the shape is 6 sq cm + 42 sq cm + 10 sq cm = 58 sq cm.)
Did anyone use a different strategy to find area? Did anyone break the shape into different smaller rectangles?
Did your strategies for finding area vary based on the shape?

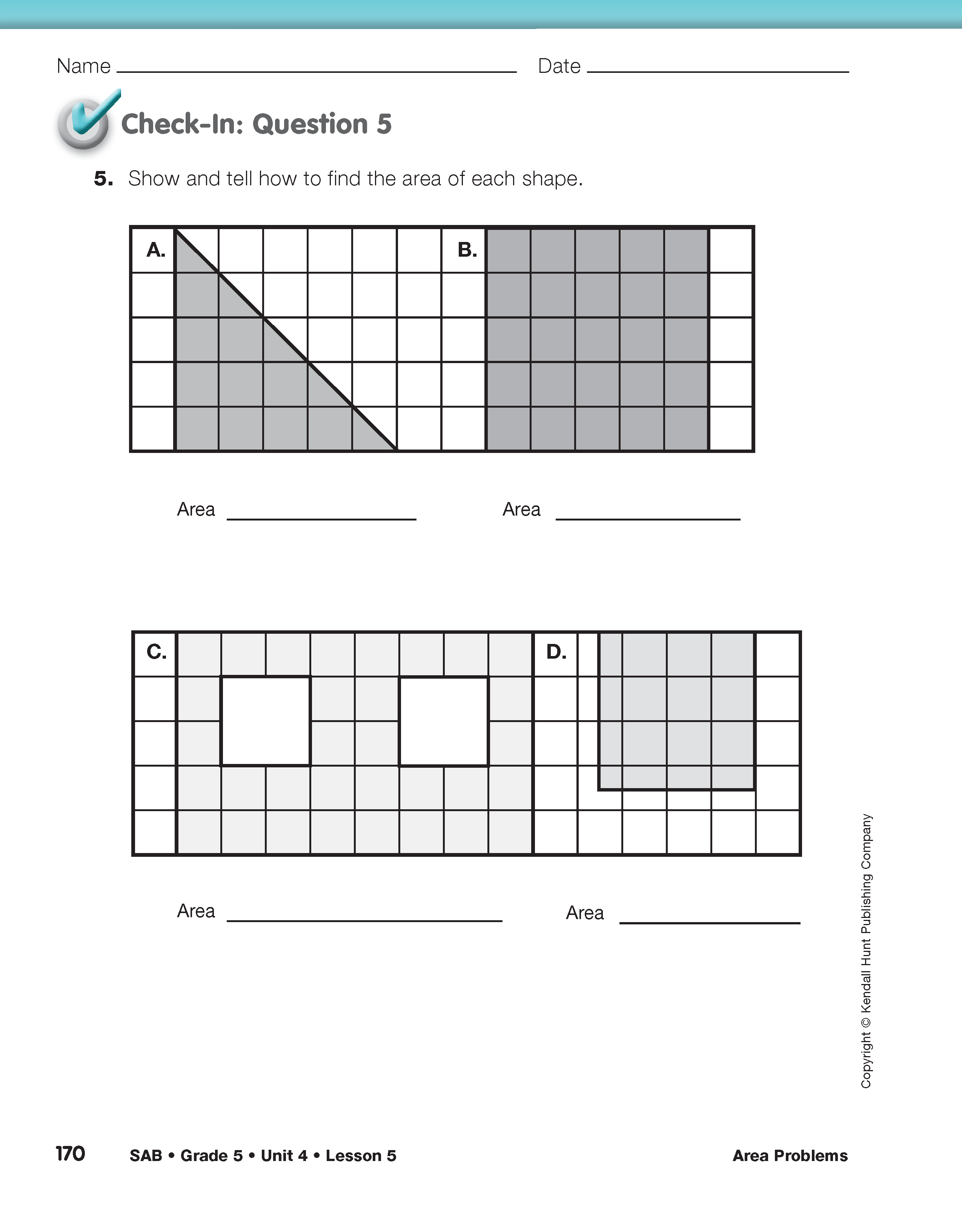
Assign Check-In: Question 5 to individual students. Students will apply strategies to find the area of several shapes.

Use Check-In: Question 5 and the Feedback Box on the Strategies to Find Area pages in the Student Activity Book to assess students' abilities to use multiplication and division strategies to find the area of rectangles or shapes based on rectangles [E8]; solve multistep problems using addition, subtraction, multiplication, and division [E7]; find a strategy [MPE2]; explain solution strategies [MPE5]; and use labels to show what numbers mean [MPE6].