Estimation and Efficient Computation
This unit focuses on the flexible use of strategies for addition, subtraction, and multiplication. A variety of models and strategies are established for computation of multidigit numbers, including number lines, rectangular arrays, expanded form, all-partials, and the compact method. Students work with these strategies to increase flexibility and efficiency. They develop estimation strategies as a way to check reasonableness of answers or to compute quickly when a problem situation arises. Students apply these computational strategies to multistep problems, including those that ask students to find the volume of rectangular prisms.
COMPUTATION METHODS

The development of computation methods in Math Trailblazers is based on the research of… read more
The development of computation methods in Math Trailblazers is based on the research of others in the field of mathematics education and our research in Math Trailblazers classrooms. Research by others corroborates the relationship between conceptual understanding and procedural fluency (Fuson & Burghardt, 2003; Fuson, 2003; Verschaffel, et. al, 2007; National Research Council, 2001; NCTM, 2000; Hiebert & Wearne, 1996). For this reason, students using Math Trailblazers first develop their own methods for each operation. With these opportunities, students make connections between their understanding of place value and procedures for computation. As stated in Adding It Up: Helping Children Learn Mathematics, “Opportunities to construct their own procedures provide students with opportunities to make connections between the strands of proficiency. Procedural fluency is built directly on their understanding. The invention itself is a kind of problem solving, and they must use reasoning to justify their invented procedure. Students who have invented their own correct procedures also approach mathematics with confidence rather than fear and hesitation” (Kamii and Dominick, 1998 in National Research Council, 2001, p. 197).
Conceptual understanding supports procedural fluency with standard procedures and algorithms as well. Therefore, students learn to represent operations with number lines or pictorial models. For the representations to be effective, students need sufficient opportunities and time to make connections between the models and numerical procedures. In summarizing findings of several researchers, the National Research Council reported, “Research indicates that students' experiences using physical models to represent hundreds, tens, and ones can be effective if the materials help them think about how to combine quantities and, eventually, how these processes connect with written procedures. The models, however, are not automatically meaningful for students; the meaning must be constructed as they work with the materials. Given time to develop meaning for a model and connect it with the written procedure, students have shown high levels of performance using the written procedure and the ability to give good explanations for how they got their answers” (National Research Council, 2001).
Throughout the unit, students share their own strategies with their classmates and read about possible strategies in the Student Guide. Comparing the various strategies and trying them out allows students to analyze the efficiency and usefulness of the methods in different situations (NCTM, 2000, p. 153).
Research in Math Trailblazers classrooms using previous editions indicates that students need support developing and using multiple computation strategies, instead of relying heavily on one procedure. Therefore, we have developed Strategy Menus for each operation to help students select appropriate methods for solving problems based on the context of the problem or the numbers involved. Students revisit strategies for addition and subtraction using the addition and subtraction strategies menus in Lesson One. They then review and apply strategies for multiplication in Lessons 2–4. See Figure 1.
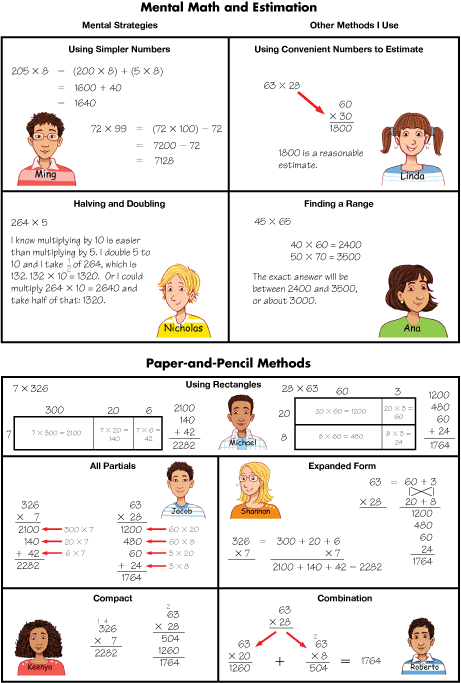
Figure 1: A menu of multiplication strategies discussed in this unit
The menus help students choose appropriate methods based on the numbers in the problems. For example, students will arrive at accurate solutions more often if they have the flexibility to solve 3001 − 2899 using a counting-up strategy, than if they use the traditional algorithm to subtract across zeros. See Figure 2. On the other hand, using the algorithm to solve 9524 − 3679 is appropriate.
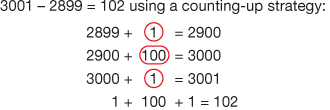
Figure 2: Choosing an efficient method to subtract
To solve the problem in Figure 3 efficiently, students need to develop skills that enable them to identify it as an estimation problem and then solve it mentally using convenient numbers.

Figure 3: Which two of the items above would provide a total of about 600 calories?
MULTIPLICATION

Students were introduced to and were provided practice with the all-partials and compact methods… read more
Students were introduced to and were provided practice with the all-partials and compact methods for multiplication in Units 4, 7, and 11 in Grade 4. Students will demonstrate varied levels of proficiency with these methods. When following rote computational procedures, it is typical to forget the underlying concepts and simply perform the algorithm. Students, however, need to understand the underlying ideas behind the algorithms so that their knowledge about multiplication can be expanded. A focus in this unit is to ensure that students have a conceptual foundation for the procedures they use to multiply multidigit numbers. To this end, students make connections between strategies and models for multiplication.
They explore mental math strategies and visual models for multiplication, they work with paper-and-pencil strategies to improve efficiency, and they develop conceptual connections between these methods. For example, students who understand the all-partials method should be able to correlate it with a rectangle model to show where each of the partial products comes from as shown in Figure 4.
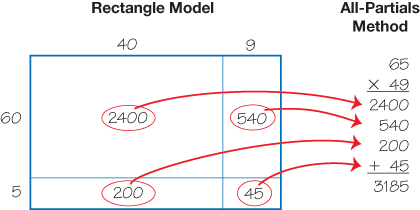
Figure 4: Connections of all-partials method to rectangular array model for multiplication
Developing varied strategies allows students to see the place-value concepts and number properties involved in multiplication. As students multiply using the expanded form, for instance, place value is highlighted as central to the process of multiplication. Students learn that procedures for multiplying 38 × 24 do not involve multiplying a “3 by a 2,” but rather 3 tens by 2 tens, or 30 by 20. Similarly, the expanded form emphasizes the role of the distributive property in multiplication; e.g., each partition of 38 (30 and 8) is multiplied to each partition of 24 (20 and 4). See Figure 5.
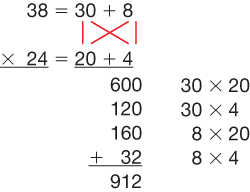
Figure 5: Expanded form for multidigit multiplication
Figure 6 shows the learning progression in this unit through multidigit multiplication. The rectangular model helps students make sense of the expanded-form method. The all-partials method, then, is developed as a shorthand version of the expanded-form method. The all-partials method is connected to the compact method so that it will not be a “black box” to students because they lack a conceptual understanding of multiplication.

Figure 6: Learning progression in multidigit multiplication
While the multiplication lessons in this unit do follow a progression similar to that shown in Figure 6, that does not necessarily mean that the compact method is always the end-goal, the best method, or even the most efficient strategy in all situations. Some students may find another method more efficient simply because they are much more likely to be accurate using it or because the numbers allow for the easy use of mental math strategies. As such, we may wish to think of these methods as a series of interconnected strategies as shown in Figure 7. Each method sheds light on multiplication in a slightly different way. Because each helps develop a deeper overall understanding of the mathematical concepts and properties involved in multiplying multidigit numbers, proficiency with one supports proficiency with each of the others.
The Math Trailblazers curriculum calls for a balanced approach to learning and practicing complex paper-and-pencil computations. Students should be able to understand the procedures they are performing, to make good estimates, and to know when to turn to a calculator for an exact answer (NCTM, 2000; National Research Council, 2001).
Since this is the capstone unit in Math Trailblazers for multiplication, it is also important for students to improve accuracy and efficiency with multidigit multiplication. Practice problems are included in the unit to build computational skills. Students should do these problems thoughtfully, using multiple methods, rather than rushing through a page of calculations without checking for errors or considering the reasonableness of their answers. If students practice incorrect procedures, it is more difficult for them to learn correct ones (National Research Council, 2001). Students also develop fluency with algorithms at different rates. Lack of fluency should not be a deterrent to moving on to different topics.
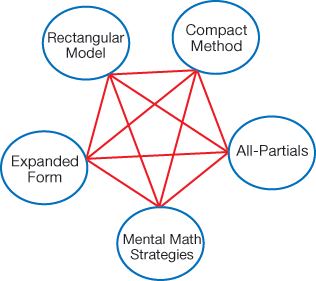
Figure 7: Learning progression in multidigit multiplication
ESTIMATION

Estimating sums, differences, and products is another focus of this unit that builds on the… read more
Estimating sums, differences, and products is another focus of this unit that builds on the estimation strategies developed in Unit 3. Estimation is treated alongside computation because both sets of skills are woven tightly together. The ability to estimate sums, differences, and products supports efficient computation and vice versa. For example, students who are comfortable estimating a product such as 78 × 41 will be able to use estimation to check that a calculation is reasonable. Since estimation and mental math strategies are often both carried out by finding convenient numbers, good estimators may become better at solving problems using mental math. Using the same example, a student who is comfortable estimating 78 × 41 as 80 × 40 may also be ready to calculate an exact product mentally, starting with 80 × 40 (80 × 40 = 3200; add 80 more to get 80 × 41 = 3280; subtract 2 × 41 = 82 to get 3280 − 82 = 3198).
In this unit, particular attention is paid to identifying the situations in which estimation can and should be used to solve problems. These include:
- Checking the reasonableness of exact computations
- Finding a quick answer mentally when an exact answer is not required
- Computing when it is difficult or impossible to find an exact answer
- Calculating with numbers that do not stay the same over time
- Calculating with numbers that are based on uncertain measurements
For some problems, students are instructed to estimate. For others, they decide whether to estimate or compute exactly, and then explain the reasoning. Ultimately, students should be able to choose from mental math, paper-and-pencil methods, and estimation to solve problems.
VOLUME

In this unit students find the volume of a rectangular prism made of cubic units using… read more
In this unit students find the volume of a rectangular prism made of cubic units using multiplication. Students begin by reviewing strategies for finding the area of a shape when you know the side lengths or for finding the side length once you know the area. They then find the area of rectangular prisms by first finding the area of the top layer of the shape. For example, the number of cubic centimeter in the top layer is just the product of 3 × 6 since there are 3 rows of 6 cubic centimeters. Thus there are 18 cubic centimeters in each layer. See Figure 8.
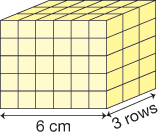
Figure 8: A rectanglar prism
Since there are 5 layers in the shape, the total number of cubic centimeters is 5 × 18 cubic centimeters = 90 cubic centimeters. The number sentence for finding the volume of a rectangular prism is expressed as:
V = l × w × h.
Within the context of volume they solve multistep problems. For example, if they know the volume and two side lengths, what is the third side length? They also solve problems involving shapes constructed with more than one rectangular prism and with shapes that have missing parts.
MATH FACTS and MENTAL MATH

This unit continues the review and assessment of the division facts to develop mental math… read more
This unit continues the review and assessment of the division facts to develop mental math strategies, gain fluency, and to learn to apply multiplication and division strategies to larger numbers. Students will focus on the division facts for the 9s.
Resources
- Fuson, K.C. “Developing Mathematical Power in Whole Number Operations.” In A Research Companion to Principles and Standards for School Mathematics. J. Kilpatrick, W.G. Martin, and D Schifter, eds. National Council of Teachers of Mathematics, Reston, VA, 2003.
- Fuson, K.C. and B.H. Burghardt. “Multidigit Addition and Subtraction Methods Invented in Small Groups and Teacher Support of Problem Solving and Reflection.” In The Development of Arithmetic Concepts and Skills: Constructing Adaptive Expertise. A.J. Baroody and A. Dowker, eds. Lawrence Erlbaum Associates, Mahwah, NJ, 2003.
- Hiebert, J., and D. Wearne. “Instruction, Understanding, and Skill in Multidigit Addition and Subtraction.” Cognition and Instruction, 14 (3), pp. 251-283, Routledge, UK, 1996.
- National Center for Education Statistics. http://nces.ed.gov/nationsreportcard/
- National Research Council. “Developing Proficiency with Whole Numbers.” In Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
- Principles and Standards for School Mathematics. The National Council of Teachers of Mathematics, Reston, VA, 2000.
- Van de Walle, J.A., and Lovin, L. Teaching Student Centered Mathematics: Grades 3–5. Pearson Education, Boston, 2006.
- Verschaffel, L., B. Greer, and E. Decorte. “Whole Number Concepts and Operations.” In Second Handbook of Research on Mathematics Teaching and Learning. F.K. Lester, Jr., ed. Information Age Publishing Inc., Charlotte, NC, 2007.











