Problem Solving with Area

Est. Class Sessions: 1–2

Developing the Lesson

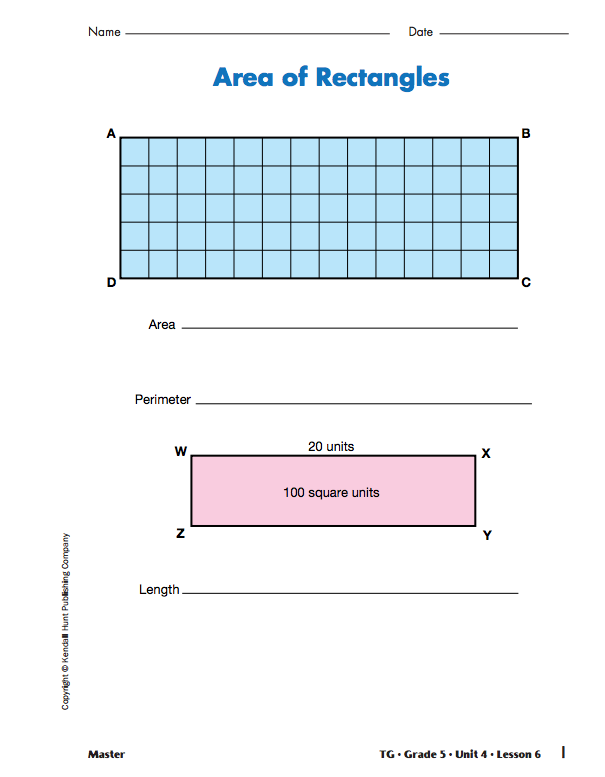
Solve Area Problems. Display the Area of Rectangles Master. Hide Rectangle WXYZ so students can focus their attention on Rectangle ABCD. Ask students to find the area and perimeter of the rectangle.

After students have had a few minutes to solve each problem, ask:

What are the attributes of a rectangle? (Possible response: a shape with four sides and four right angles; opposite sides are parallel and are equal in length)
How can you use what you know about a rectangle to help you find the perimeter of the rectangle? (Possible response: Perimeter is the distance around the edge of the shape and in a rectangle two sides are the same. 5 cm × 2 + 14 cm × 2 is the perimeter; I added the length and the width and knew the other length and width are the same so I multiplied that number by 2 to get the perimeter.)
How did you label the perimeter? (centimeters) Why? (Possible response: I am counting the number of centimeter lengths.)
How did you find the area? (Possible response: I multiplied the number of rows of square centimeters by the number in each row.)
How did you label the area? (square centimeters) Why? (Possible response: I am counting square centimeter units when I am measuring area.)

Show students Rectangle WXYZ and ask students to find the length of the rectangle.

Ask:

What do you know? (Possible response: I know the area is 100 square units and one side of the rectangle is 20 units.)
What do you need to find out? (the length of the rectangle)
What are going to do? (Possible response: Divide the area by 20 units to find the length of the rectangle.)

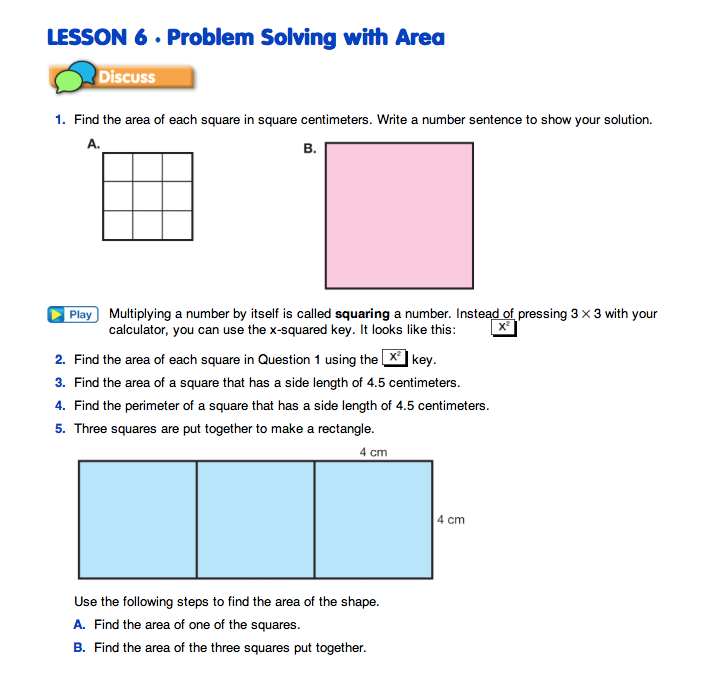
After this quick review, direct students to the Problem Solving with Area pages in the Student Guide. Ask students to complete Question 1.

Use these or similar prompts to discuss Question 1:

How are the two squares in Question 1 different? (Possible response: One square is smaller than the other. One of the squares has grid lines and the other is shaded.)
What strategies can you use to find the area of the smaller square? (Possible responses: You can quickly count the squares in the grid. Since each side is 3 centimeters long you can multiply 3 × 3 to find the area.)
What is the number sentence you used to show the area of the smaller square? (3 centimeters × 3 centimeters = 9 square centimeters)
What do you need to do first in order to find the area of the larger square? (You need to measure the length of the sides.)
How many sides do you need to measure? Explain your reasoning. (You only need to measure one side. Since it is a square, all of the sides will be the same length.)
What is the length of one of the sides of the larger square? (5 centimeters)
What is the number sentence you used to record the area of the larger square? (5 centimeters × 5 centimeters = 25 square centimeters)

After completing Question 1 ask students to find the x² key on their calculators. Students should be familiar with this key from previous lessons. Discuss Question 1–4. In Question 2, students are directed to practice using the x² key to find the area of the two squares in Question 1. Check to make sure students understand how to use this key on their calculators before asking them to complete Question 3. In Question 3, students should use their calculators to find that the area of the square is 20.25 square centimeters. In Question 4, students are asked to find the perimeter of a square. Ask students to share their strategies for solving this problem.

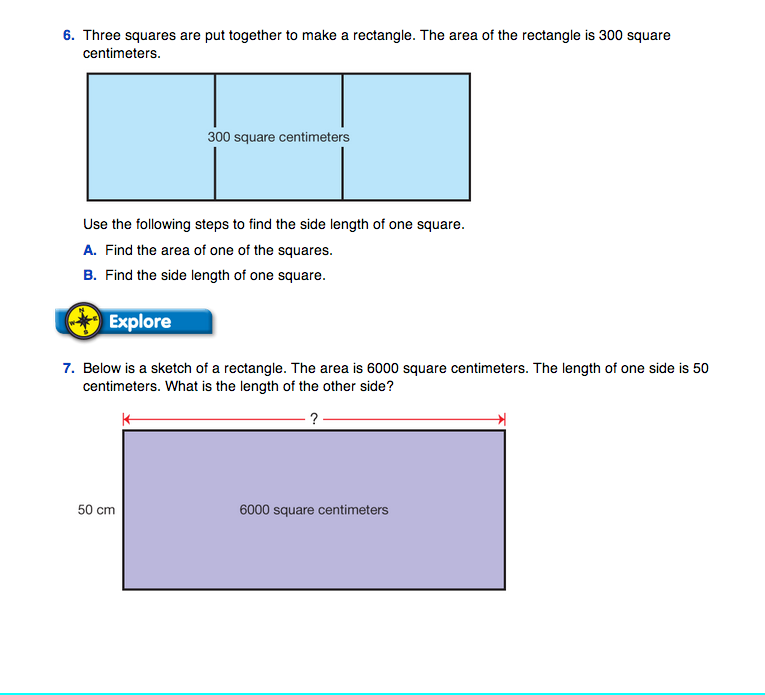
Students use multiplication and division to solve multistep problems involving area in Questions 5–7. As students complete each step of a problem, encourage them to share their reasoning. In Question 5, students find the area of a rectangle composed of three squares by first finding the area of one of the squares. Ask several students to share their strategy for finding the area of the rectangle. Students should reason that if they know the length of one side of one of the three squares they can find the area of that square and then multiply it by 3 to find the area of the rectangle. Students can use this reasoning to answer Question 6 by first realizing that if the total area of the rectangle is 300 square centimeters, the area of one of the squares will be 1/3 of that or 300 square centimeters divided by three.

Upon completion ask:

If you know the area of the total rectangle is 300 square centimeters, how will you find the area of one of the three squares? (Possible response: I can divide the area of the rectangle by 3 to find that the area of one square is 100 square centimeters.)
What strategy can you use to find the side length of one square once you know the area? (Since all the sides of the square are the same length, once I know the area I can think about what number I square or multiply by itself to equal 100.)
What number can you square to equal 100? (10)

Reason about Area. Questions 7–11 provide students with an opportunity to use what they have learned about area to solve problems. Students are asked to find the length of a side of a rectangle when given the total area and the length of one of the sides in Question 7.

After reading the question, ask:

What two operations can you use to help you solve this problem? (multiplication and division)
How can you use multiplication to find the missing side length of the rectangle? (Possible response: You can think about what number times 50 will equal 6000.)
How can you use division to find the missing side length? (Possible response: You can divide 6000 by 50 to find the length of the missing side.)
What is the length of the other side of the rectangle? (120 centimeters)

In Questions 8–11, students need to read the information carefully to decide if it describes a possible rectangle or if it is “crazy.” If it is possible, they solve the problem, and if it is crazy, they use what they know about rectangles to explain why. Questions 8, 9, and 11 each describe a problem that is possible to solve. After reading Question 10, students should recognize that the measurements given are not possible for a rectangle because in a rectangle opposite sides are equal in length. There cannot be three different side lengths.

Solve Multistep Problems. Students work with a partner to complete Questions 12–15. These questions are multistep problems involving area. Before students begin work on these problems, direct them to the Math Practices page in the Student Guide Reference section or to the display of the Math Practices page. Ask student to look at the first Math Practice, Know the problem. Have students talk with a partner and identify what they need to “know” about a problem.

After a few minutes, ask:

What are some strategies you can use to help you “know” a problem? (Possible responses: You need to read the problem carefully so you know what information is important. You need to look carefully at the question to know what you have to answer. You should follow each step of the problem carefully so you can find the final answer.)

As students work on Questions 12–15, circulate among the groups using these or similar questions to encourage students to share their problem solving strategies:

What was the important information you were given in this problem?
What do you already know about the shape in this problem?
What question do you need to answer?

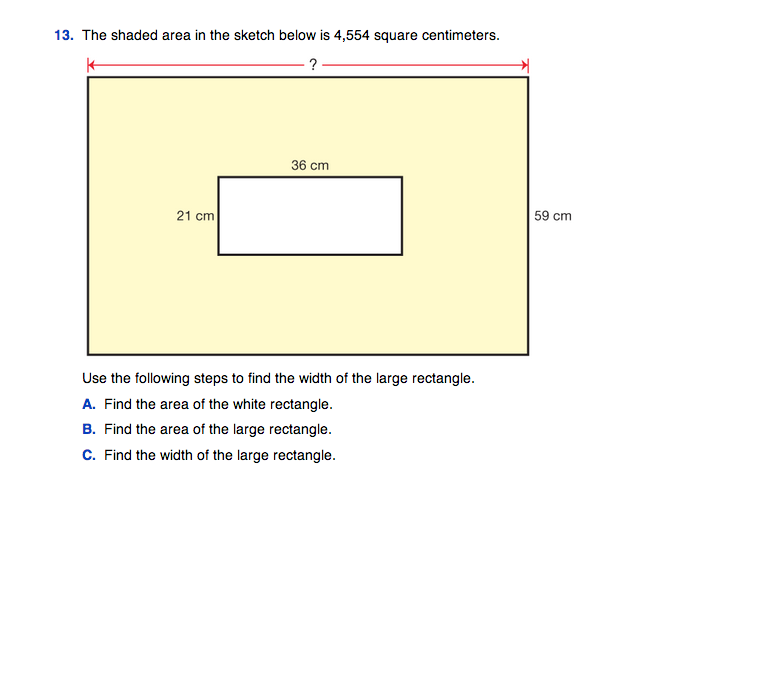
Questions 12–13 provide students with specific steps to help them solve the problem. For Question 14, students need to identify the steps they will take to find the total area of the shape. In Question 15, students evaluate the reasoning of another student's solution strategy.