Use Benchmarks to Estimate. Show the class your
collection of connecting cubes. See Materials
Preparation. Tell students that they are going to help
you count the cubes to find out how many the class
has in all. First, however, they will estimate the total
number of cubes in your collection.
Show them your
referent bags of 10 and 100 cubes and ask:
- Do you think 20 is a good estimate for the entire
collection of cubes? (no) Why or why not? (Possible response: 20 is less than 100 and I can
tell that there are a lot more than 100 cubes by
looking at the plastic bag.)
- Would 120 be a good estimate? Why or why not?
- Would ten million be a good estimate? Why or why
not? (No, that is way too big of a number.)
- How does looking at the bags of 10 and 100 help
you make a good estimate? (Possible response: I
think of how many 100s are in the collection.)
- What is an example of a "crazy" estimate for the
cubes? (Estimates would be either very small or
very large. An estimate of five or an estimate of a
million are both "crazy" estimates.)
Ask student pairs to estimate the number of cubes in
the collection and to record the estimate in Question
1A of the About How Many Cubes pages in the
Student Activity Book. Students should explain how
they determined their estimate in Question 1B with
words or drawings. Remind them to describe any
way they used tools, such as the referent bags in
their explanations (MPE2, Find a strategy, and
MPE5, Show my work).
- What are some good estimates for the number of
cubes in our class collection? Why do you think
so?
Write their estimates in a list on the board or on
chart paper. After the cubes have been counted, students
will answer Question 2 and compare their estimates
with the actual count. Tell students to look at
the list and note where the estimates cluster.
- Is there an interval in which most of the estimates
lie?
- If so, what is that interval?
Use the About How Many Cubes pages and the Feedback Box
in the Student Activity Book to assess students' abilities to
estimate the number of objects in a group using 10 and 100
as benchmarks [E4]; find a strategy [MPE2]; and show work
[MPE5].
When you distribute connecting cubes, ask students to
arrange them in stacks of ten. Keeping the cubes organized
this way assists in the efficiency and management of the
lesson. Before you collect the cubes, ask students to arrange
them into stacks of ten so they are ready for the next day of
instruction.
Group and Count Cubes. Distribute all the cubes
among student pairs for counting. Each pair should
have between 60 and 80 cubes. Allow students time
to explore and share different ways they can group
the cubes in order to count them.
- What would be a good way to count the cubes?
- What are the different ways you can group the
cubes to make your counting easier? (Possible
response: I can group the cubes by tens.)
Then ask them to recall how they counted the total
number of buttons from the class collection in
Unit 2. Help them to remember that they grouped the
buttons into tens and placed them into cups. When
students had ten cups full of ten buttons each, they
poured the cups into a plastic bag. Each plastic bag
had one hundred buttons in all. Tell students that
they will count connecting cubes the same way.
They will group by tens to see the place value implications.
Ask questions like the following:
- Why do you think we ended up putting the buttons
into groups of ten? (It was easier to count a big
quantity.)
- Why does grouping by tens make it easier to
count? (It is easy to skip count by tens.)
- What if you have some that are extra, some that do
not fit into a ten? (Those are the leftovers.)
- How do you count the leftovers? (by ones)
- Is it possible to have one leftover? (yes)
- Is it possible to have 7 leftovers? 0 leftovers?
2 leftovers? Why or why not? (All of these are
possible leftovers.)
- What happens when we have 10 leftovers or
12 leftovers? (If we have 10 or more leftovers, we
can make another group of ten.)

Up to now, students have been free to use whatever
groupings work best for them when they are counting large
numbers, although grouping by tens has been encouraged.
With this activity, students need to group by tens so they
begin to see the place value implications. You may observe
students who are still more comfortable grouping by twos or
fives and who are reluctant to move to grouping by tens.
Emphasize to these students the importance of grouping by
tens. Help them learn to consolidate their groups of two or
five into groups of ten. Have them skip count their stacks of
ten aloud with you.
Group by Tens and Ones. Instruct student pairs to
group the cubes into stacks of ten and leave the individual
leftover cubes loose. To determine the number
of cubes, students count the stacks by skip
counting by tens and count the leftovers by ones.
In your discussion, make an effort to use the number of tens
and the actual number interchangeably, e.g., 7 tens and 70,
so that students develop a habit of thinking of 7 tens as 70
and vice versa.
It is important, however, to keep the units clear as you talk
with students. For example, 6 stacks of ten have 60 cubes.
In this case, it would be incorrect to write 60 in the
"Stacks of 10" column in the recording chart as this would
mean 60 stacks of ten.
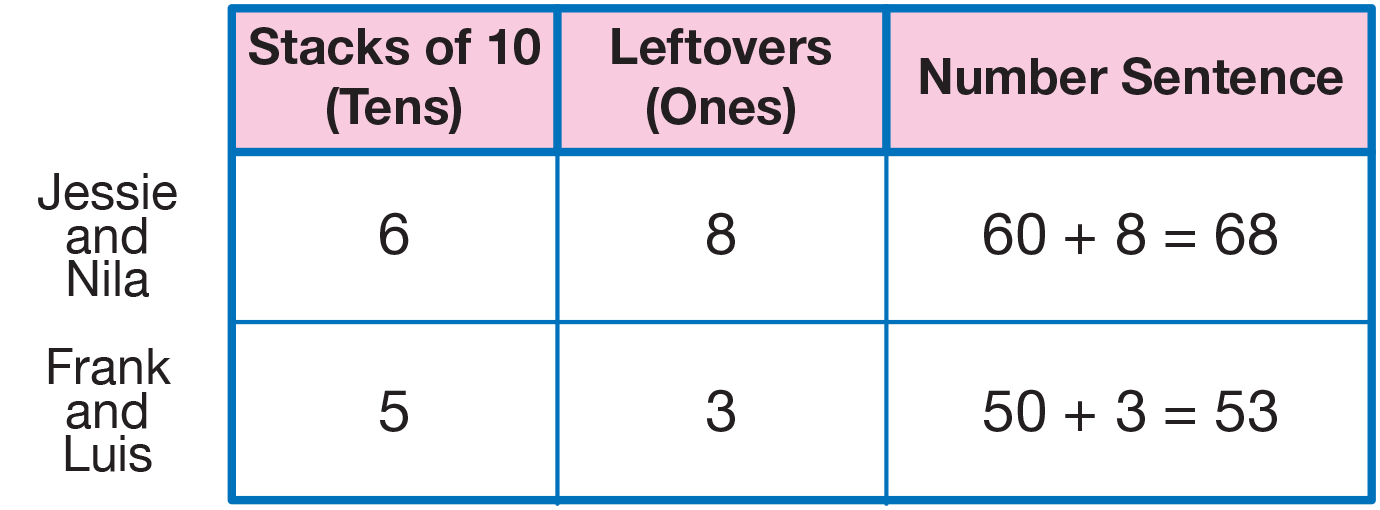
Display the Tens and Ones Recording Chart Master.
Ask each pair how many stacks of tens they have
and how many leftovers. Then ask someone else to
give the number sentence.
For example, referring to
the sample chart in Figure 1, ask:
- Jessie and Nila, how many stacks of ten do you
have? (6 stacks)
- How many cubes is that? (60 cubes) [Record 6 on
the recording chart in the "Stacks of 10" column.]
- How do you know? (It is 6 tens: 10, 20, 30, 40,
50, 60.)
- How many leftovers do you have? (8 leftovers)
[Record 8 in the leftovers column.]
- Luis, what is a number sentence that shows Jessie
and Nila's cubes? (60 + 8 = 68) [Record the
number sentence.]
Plan to Find Class Total. After you have recorded
the results for all pairs in the classroom, ask students
for ideas about how to proceed.
- How can we put all this together so that we know
how many cubes we have in all?
Let students think a minute and offer suggestions.
Ask them to explain how their suggestion would
work and why their plan is a good one. Let students
comment on suggestions made by other students.
Students could generate several different plans. Most
likely they will suggest putting all the tens in the
class together to make hundreds because that is how
they counted the collection of buttons in Unit 2. That
is the method discussed below. However, there are
other possible scenarios and we discuss how to manage
those alternative ways as well.
If students suggest putting all the cubes together to
count them, encourage them to think about the
details for how it would work.
- How do we put all our cubes together?
- How is that different from the collection of cubes
we had at the beginning, before we did any counting?
Remember, the cubes were all together then.
- Are you suggesting counting by ones?
- What should we do first?
- Can we use the counting we have already done in
pairs? How?
Group Tens to Make Hundreds. Guide students to
a process in which the pairs keep their stacks of ten
together and bring them to the front of the class to be
consolidated with those of the other students.
- How can we count all these stacks of ten? (skip
count by tens)
Count along with the students as pairs bring their
stacks of ten.
When you get to 100, ask:
- What should we do now? What did we do with
100 buttons so we could keep track? (Put them in
a plastic bag or rubberband them together.)
Group the stacks of ten into bundles of one hundred.
Secure bundles of one hundred with a rubber band or
place each group of 100 in a gallon-sized resealable
bag and gather them in one area. Cluster the extra
stacks of ten (that don't add up to another 100)
together.
- What can we do with these?
- Are we close to another 100?
- How many more stacks of ten do we need to make
another 100?
- Some of you have leftovers. What should we do
with the leftovers? What would be a good way to
count them? (We can put them together to make
more tens.)
Ask students to bring their leftover cubes up. Have a
student pair act as assistants and stack the leftovers
into tens as they come up.
- [Student name] has [ 6 ] leftovers. How many more
does he need to make a ten?
- Who can contribute leftovers to make a ten?
- [Student name] had [ 7 ] leftovers. She has given
[Michael] [ 4 ] cubes to make a ten. How many
does she still have? How many more do we need
to put with [student name]'s to make another ten?
Once all the possible stacks of ten have been made,
ask a volunteer to count them, skip counting by tens.
Ask students whether there are now enough tens to
make another group of 100. If so, make another
group of 100 and move it to the hundreds pile.
Ask a student volunteer to come forward and count
the number of groups of one hundred. The class can
count along as the volunteer counts. After the groups
of 100 have been counted, ask questions similar to
the following.
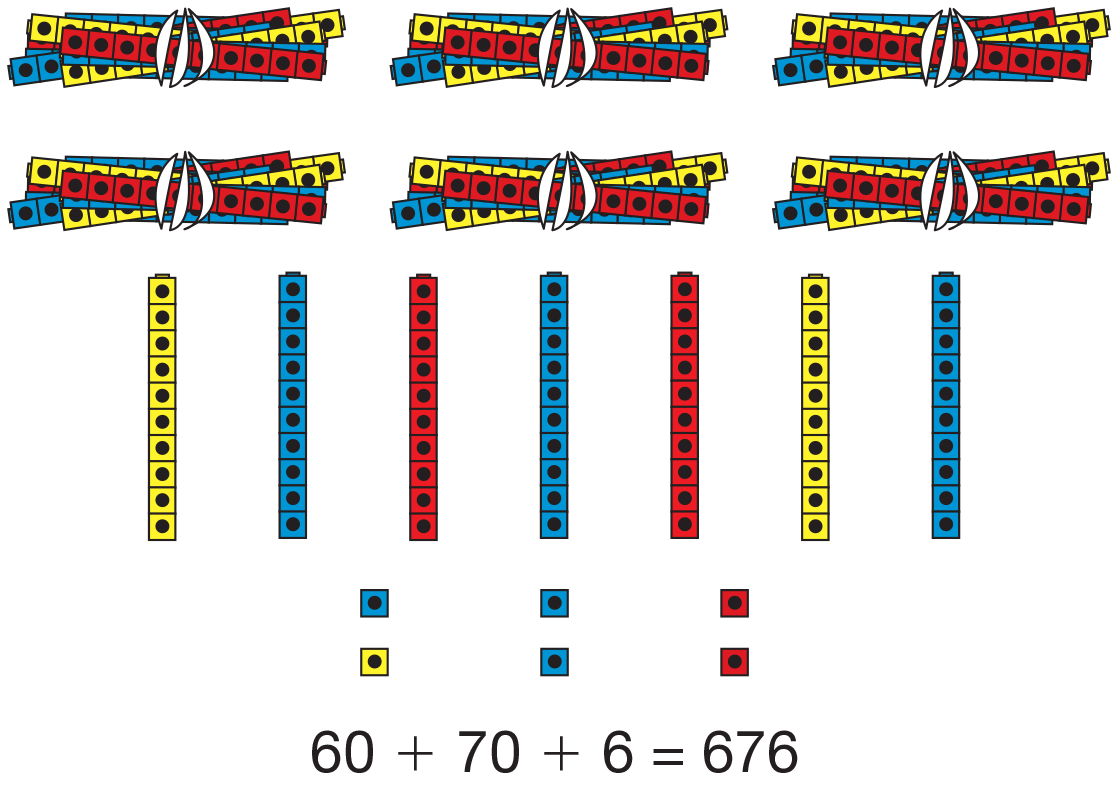
For example, if the total number of
cubes is 676, ask:
- How many groups of 100 do we have? (6 groups
of 100)
- How many cubes is that? (600 cubes)
Write 600 on the board or on chart paper. Have
another volunteer count the stacks of ten.
- How many stacks of ten do we have? (7 stacks of ten)
- How many cubes is that? How do you know? (70 cubes; you can count by tens.)
Write 70 to the right of the 600. Have a third volunteer
count the leftovers.
- How many leftovers do we have? (6 leftovers)
Write a plus sign between the 600 and the 70 and
between the 70 and the 6.
- How many cubes do we have in all? (676 cubes)
- What number sentence describes our cubes? (600 + 70 + 6 = 676 cubes)
Point to each column and have the students read
with you as you say: "Six hundreds, 7 tens, 6 leftovers
or ones. 600 plus 70 plus 6 equal 676." See
Figure 2.
Have students check the total number of cubes by
using a calculator to add the total number from each
pair recorded on the board or chart paper. Since it is
easy to press incorrect keys, have one student in
each pair say the numbers slowly and the other
repeats as he or she presses each calculator key.
Compare the running totals after each number is
added.
Alternative Ways to Find Total. As mentioned earlier,
students may suggest alternative ways of calculating
the total number of cubes. For example,
students may suggest using the recording chart alone
to calculate the total. Ask them to describe how they
would use the chart to figure out how many cubes
there are in all. They may have some interesting
strategies for using the numbers on the chart.
Students can skip count the tens, marking on the
sheet when they reach each hundred, then add the
leftovers. Students may also suggest simply using a
calculator to add up the numbers. Suggest to students
that the calculator will be a good way to check
their total at the end, but first they should figure out
a method that uses the mathematical strategies and
tools they have been practicing.
Another possible suggestion is that pairs could combine
their cubes with those of other pairs and make
ever-larger groups until all the cubes for the whole
class are grouped together. If your students choose
this method or something similar, make a new class
recording sheet for each new consolidation. See the
Sample Dialog.

The following dialog suggests prompts to ask students about
how they dealt with leftovers when combining their cubes.
Teacher: How many tens do the four of you have?
Jessie: Nila and I have 6 tens.
Frank: Luis and I have 50 cubes.
Teacher: How many tens is that, Frank?
Frank: 5 tens.
Teacher: How many tens do you have altogether?
Nila: 11 tens altogether.
Teacher: How many cubes is 11 tens? How can we figure
that out?
Jessie: I can skip count by tens.
Nila: I look at the 200 Chart. Eleven tens is 110 cubes.
Teacher: How many leftovers do you have together?
Luis: 8 and 5. That's 13.
Teacher: Can you make another ten with your leftovers?
Luis: Yes. So now it's one ten with 3 leftovers.
Teacher: Yes! So that makes how many tens altogether?
Jessie: 12 tens.
Teacher: And how many cubes is 12 tens?
Nila: It's like 12 rows on the 200 Chart. 10, 20, 30, 40, 50,
60, 70, 80, 90, 100, 110, 120. 120 cubes.
Teacher: If you have 3 leftovers, how many more cubes
would you need to make another ten?
Frank: I think 7, because 7 + 3 = 10.
Teacher: That's right!
Assess Estimates. After students verify the total, ask
them to look back at the original estimates. Ask
them to identify the highest estimate and the lowest
to determine the range and write the two numbers in
a separate space. See Content Note.
- Does the total number of cubes fall within the
range of our class estimates?
- Does the total fall nearer to the top of the range?
The middle? The bottom?
- Does it fall within where we decided the estimates
clustered?
- Now think about the estimate you made in the
beginning of the lesson.
We are using an everyday understanding of range which
differs slightly from the mathematical definition. In
mathematics, range is defined as the difference between the
highest number and the lowest, indicating subtraction. For
example, in a list of numbers where the highest number is 25
and the lowest is 17, the mathematical range is 25 − 17, or 8 (numbers). In everyday speech, it is common to say the
numbers range from 17 to 25, or that the range is 17 to 25.
This usage implies 9 numbers and includes both beginning
and ending numbers (17, 18, 19, 20, 21, 22, 23, 24, 25).
Have students return to the About How Many Cubes
pages in the Student Activity Book and complete
Question 2. They will record the total number of
cubes in the class collection and assess the reasonableness
of their estimates.
- How did you determine if your estimate was reasonable
or not [Question 2B]? (See Content
Note.)
- What if your estimate was off by 100 cubes? (That
would be unreasonable.)
- What if your estimate was off by 10 cubes? (That
would be reasonable.)
Consider the following questions when assessing the
reasonableness of an estimate for quantity:
- What is the size of the unit in relation to the total
amount of items? (For example, it is more difficult to
accurately estimate 100 grains of rice compared to
100 connecting cubes.)
- How much of the quantity can be seen? (It is more
difficult to estimate the quantity of items if they are out
of sight.)
- How inaccurate is the estimate in relation to the total
number of objects? (In the case of 500 cubes, an
estimate that is off by 100, an estimate of 400, is
inaccurate. However, if there are 5000 cubes, an
estimate that is off by 100, an estimate of 4900, would
be highly accurate.)