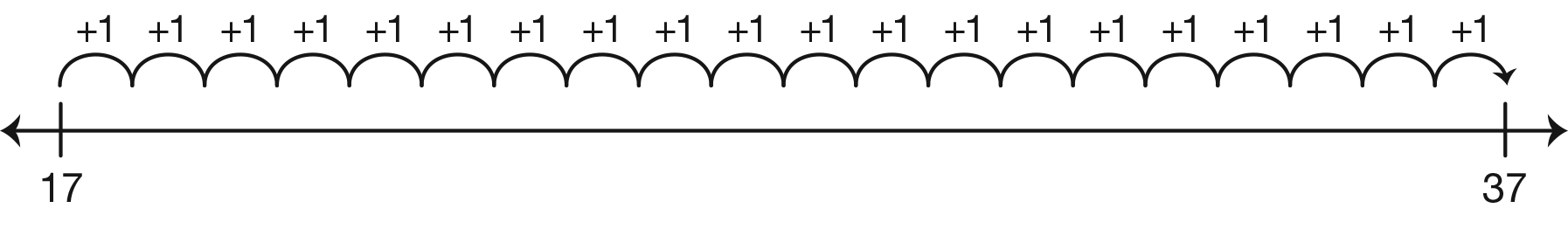Introduce Base-Ten Hoppers. Use a display of the
Base-Ten Hoppers pages in the Student Activity Book
to introduce the base-ten hoppers. Ask students to
work in pairs to study the moves that the base-ten
hopper can make by looking at the four number lines
in Questions A, B, C, and D. Tell them that the base-ten
hopper is a creature who hops on number lines.
He can do some hops but not others. You need the
students to help you understand what kinds of hops
this creature can and cannot do.
Discuss the fact that the number lines are "open"
number lines.
- What do you notice that is different about these
number lines? (Possible response: They do not
have all the numbers written below the number
line, only those numbers where the base-ten hopper
hops.)
- How can you tell how far the base-ten hopper has
hopped? (Possible response: The number above
the hop tells how far each hop is. Or I can subtract
the start of the hop from the end of the hop.
For example, in Question A, it hopped from 10 to
20 in one hop. 20 minus 10 is 10 so I know it
hopped ten spaces.)
- How can you tell which direction the base-ten hopper
hopped? (It says a plus [+] if it hopped forward
and it says a minus [−] if it hopped
backward.)
- How far can the base-ten hopper hop in one hop?
How do you know? (The base-ten hopper can
make hops of ones and tens. Possible response:
In Question A, the base-ten hopper made hops of
ones and tens.)
- Where else have we worked with tens and ones? (Possible responses: We put buttons and marshmallows
in groups of tens and ones; we made
stacks of tens and groups of one with connecting
cubes; we partitioned numbers into tens and
ones.)
- Where do you think the base-ten hopper can start
on the number line? Do you think it can start anywhere
on the number line? Why do you think so? (Possible response: The base-ten hopper can
probably start at any number on the number line.
In Question A, the base-ten hopper started at 0.
In Question B, the base-ten hopper started at 25.
In Questions C and D, the base-ten hopper
started at 14.)
- Where do you think the base-ten hopper can stop
on the number line? Do you think it can stop anywhere
on the number line? Why do you think so? (Possible response: The base-ten hopper can
probably stop at any number on the number line.
You can make any number using tens and ones.)
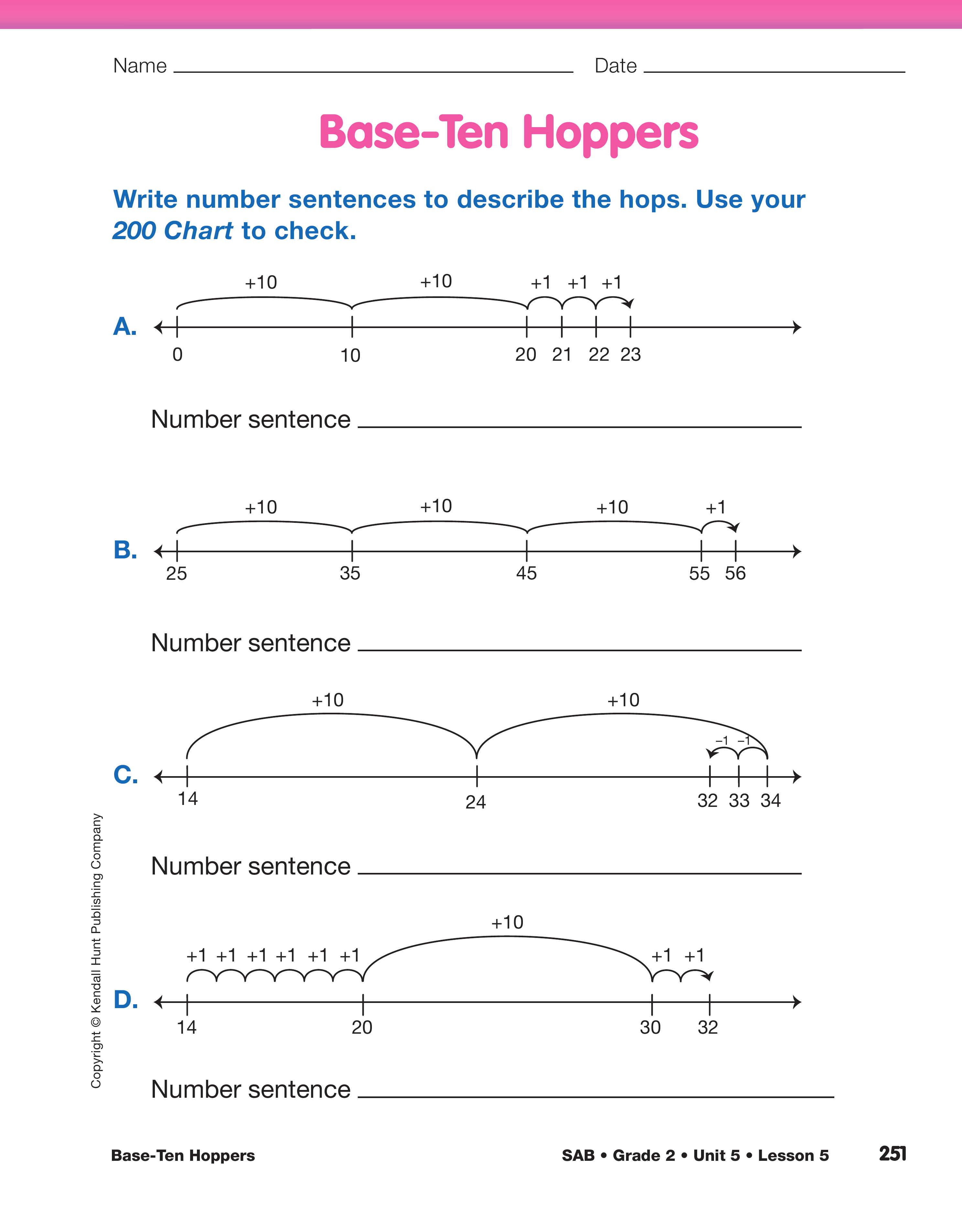
Direct students' attention to Question A.
- Look at Question A. What is a number sentence
that describes the base-ten hopper's moves? (Possible response: 10 + 10 + 1 + 1 + 1 = 23
or 10 + 10 + 3 = 23)
- If we included zero, what would the number sentence
be? Where did this hopper start? (at 0; 0 + 10 + 10 + 1 + 1 + 1 = 23 or
0 + 10 + 10 + 3 = 23)
- Does the answer change? (no)
- When a hopper starts at zero, do you always have
to put zero in the number sentence? (no)
- Use your desk number line to show how each hop
on the number line is in the number sentence as I
say the sentence out loud:
0 + 10 + 10 + 1 + 1 + 1 = 23.
- How do the hops in Question A show the "counting
on" strategy to add? (Hops of one are the
same as counting on by ones.)
- What do the hops of ten remind you of? (skip
counting by tens)
Direct students' attention to Question B.
- Look at Question B. Where does the base-ten
hopper start? (on 25)
- Do you have to include the starting number in this
sentence? Why or why not? (You have to include
the starting number in this case because the
hopper does not start at 0.)
- What is the number sentence? (25 + 10 + 10 + 10 + 1 = 56)
- Show these hops on the class number line as I say
the number sentence out loud: 25 + 10 + 10 + 10 + 1 = 56.
Direct students' attention to Question C.
- Describe what the base-ten hopper did in
Question C. Where did it start? Where did it stop? (The base-ten hopper started at 14 and hopped
forward two tens to 34: 14, 24, 34, and hopped
back two ones to land on 32.)
- What number sentence describes the hops in
Question C? (14 + 10 + 10 − 1 − 1 = 32 or
14 + 10 + 10 − 2 = 32)
- When the base-ten hopper was on 14 and wanted
to hop 10 spaces in one big hop, where did it
land? Why? (Possible response: on 24; I know
from using the 200 Chart that when you add ten,
the next number has the same last number.)
- What tool have we used that makes it easier to add
10 and subtract 10? (200 Chart)

Moving forward (or back) to the nearest convenient number,
as in the example in Question D, allows for skip counting by
tens with multiples of ten, something that students are
familiar with.
When reading the descriptions of a base-ten hopper's moves
on a number line, make sure students understand the
difference between "move forward" and "move to." For
example, in Question E of the Base-Ten Hoppers page, the
hopper starts at 17 and moves forward 20. Students can
misinterpret that to mean the hopper starts at 17 and lands
on 20.
Direct students' attention to Question D.
- Describe what the base-ten hopper did in
Question D. (The base-ten hopper started at 14,
hopped six ones to 20, hopped one ten to 30 and
hopped forward two ones to 32. See Content
Note.)
- What number sentence describes the hops? (14 + 6 + 10 + 2 = 32)
- What is the same about the lines in Questions C
and D? (The base-ten hopper started at 14 on
both lines, and stopped at 32 on both lines. It
started and stopped at the same place.)
- What is different about the lines in Questions C
and D? (The moves are different.)
- In Question C, how far is it from where the baseten
hopper started to where it stopped? (The
base-ten hopper started at 14 and stopped at 32. It
moved forward 18.)
- In Question D, how far is it from where the baseten
hopper started to where it stopped? (The
base-ten hopper started at 14 and stopped at 32.
Between 14 and 32 is 18.)
- Are the distances the same? How do you know? (Yes. The base-ten hopper started at 14 and
stopped at 32 on both lines.)
- Is this a true number sentence:
14 + 10 + 10 − 1 − 1 = 14 + 6 + 10 + 2? (Yes; Possible response: Both sides of the equal
sign show two different ways to get to the same
place.)
- Talk with your partner. Which number line in
Questions A–D is easier for you to understand?
Why do you think the base-ten hopper chose to
hop the way it did on each number line? (Possible
response: In Question C the hopper didn't have
to make as many hops. In Question D, it hopped
to 20 first, so it would be easier to know where
the next ten was.)

You may have students who are unable to work on an open
number line because they need the structure of seeing all the
numbers on the line before solving the problem. For those
students, make copies of the Number Line 0–40 Master for
drawing the hops. Make sure they also have their 200 Charts
available for reference.
Use Hoppers on Number Lines to Solve Problems. Display and direct students' attention to
Questions E–H on the Base-Ten Hoppers pages.
Read the description of the hopper's moves in
Question E. See Meeting Individual Needs. Have
students work in pairs to complete the question. Let
students experiment with ways to solve the problems.
Encourage students to use their desk number
lines or 200 Charts to help them know where they
will land after each hop.
Discuss Question E after students have had a chance
to find ways to start at 17 and move forward 20. Use
a display of the Open Number Lines Master to facilitate
discussion. As students find one way, have them
find a second way, giving a number sentence for
each way. Possible strategies include:
- Hopping by ones forward, so that 20 individual
hops are shown. (17 + 1 + 1 + 1 + 1 + 1 + 1
+ 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 +
1 + 1 + 1 + 1 = 37. See Figure 3.)
- Making two hops of ten: from 17 to 27, then 27
to 37. (17 + 10 + 10 = 37. See Figure 4.)
- Making three hops of one to 20, then a long hop
of ten to 30, then seven hops of one to 37. (17 +
1 + 1 + 1 + 10 + 1 + 1 + 1 + 1 + 1 + 1 + 1
or 17 + 3 + 10 + 7. See Figure 5.)
Some students may readily see that with one hop of
20 the hopper will land at 37. While this is not
strictly a move of tens or ones, 20 is a multiple of
ten and should not be discouraged if students understand
and can explain their thinking. See Content
Note. Encourage students to ask one another questions
until all the solutions are clear.
- Does everyone understand how each of the hoppers
moved? Do you know where each hopper
landed after each hop? Is it clear what direction
each hopper moved? Do you need to ask anyone
a question?
- How are the number lines alike? (The hoppers all
stop at the same place, 37.)
- How are they different? (Possible response: Some
hoppers went by ones, some hoppers went by
tens and ones. They made different moves to get
to the number, 37.)
Assign Questions F–H. As student pairs work,
circulate and ask:
- What do you think about the different ways?
Which one do you like best and why? Which are
easiest to understand? Which use fewer hops? Possible responses may include:
- Hopping by ones is easiest to understand, but you
might make a mistake counting and it takes a
long time to show all the hops and where they
land.
- It is pretty easy to hop by tens. We knew from
moving on the 200 Chart that ten more than 17 is
27 and ten more than 27 is 37.
- We looked at our desk number line to find the
next number when you count by tens. It was 20.
That made it easier to go ten more.
Allow students flexibility in showing their moves on the
number line. The big idea is to think in tens and ones. Some
students may move by multiples of ten (20, 30, etc.). Other
students may find it cumbersome or impossible to write all
the numbers under the number line where the hopper lands.
Encourage students to simply make their drawings clear as
they explore various ways of moving in tens and ones.