Develop a Unit of 10

The Marshmallows and Containers lab in Lesson 2 creates a natural context for students to group, count, and compare large numbers of objects. Students have been grouping and counting objects and distances to develop a unit of 10 ones. They have been using the language of ones and a group of ten. In this unit, students transition from thinking about a group of ten objects to one unit of ten. The language also transitions to ones, tens, and hundreds. This is an important step in students' journey to understanding the units that organize our base-ten number system.

Students will snap cubes together to make groups of ten and represent them as tens. The reorganized cubes will help students' partition numbers specifically into groups of ones, tens, and hundreds. Students will also represent these partitions in number sentences

Showing Different Partitions

The value of manipulatives in helping students understand our system of writing numbers is generally accepted in the mathematics education community. The way in which manipulatives are used and the type of manipulative used have a significant effect on understanding. The grouping of the connecting cubes in Unit 5 and the use of base-ten pieces in Unit 6 lay the foundation for place value understanding. Students become aware of the relationships between the values represented in neighboring columns. For example, they come to realize that a 3 in the hundreds place is worth ten times more than the 3 in the tens column, and the 3 in the tens column is worth ten times more than a 3 in the ones column.

Through data from classroom observations, student interviews, and tests in the Math Trailblazers Research and Revision Study, we found that students can represent numbers using base-ten pieces and accurately add and subtract. However, we found that they need more opportunities to explore the partitioning of numbers into groups of hundreds, tens, and ones in order to understand that different partitions of the same number have the same total (e.g., 45 = 40 + 5 = 30 + 15). This understanding is important in developing flexible and efficient methods for addition and subtraction that require composing and decomposing numbers or regrouping. For this reason, in Unit 5, students develop strategies for grouping and counting large numbers of connecting cubes into bundles of hundreds, stacks of tens, and leftover ones. They write the numbers of each group on recording sheets that focus their attention on the value of each group. This helps reinforce the concept that different partitions of the same number have the same total. See Figure 1.

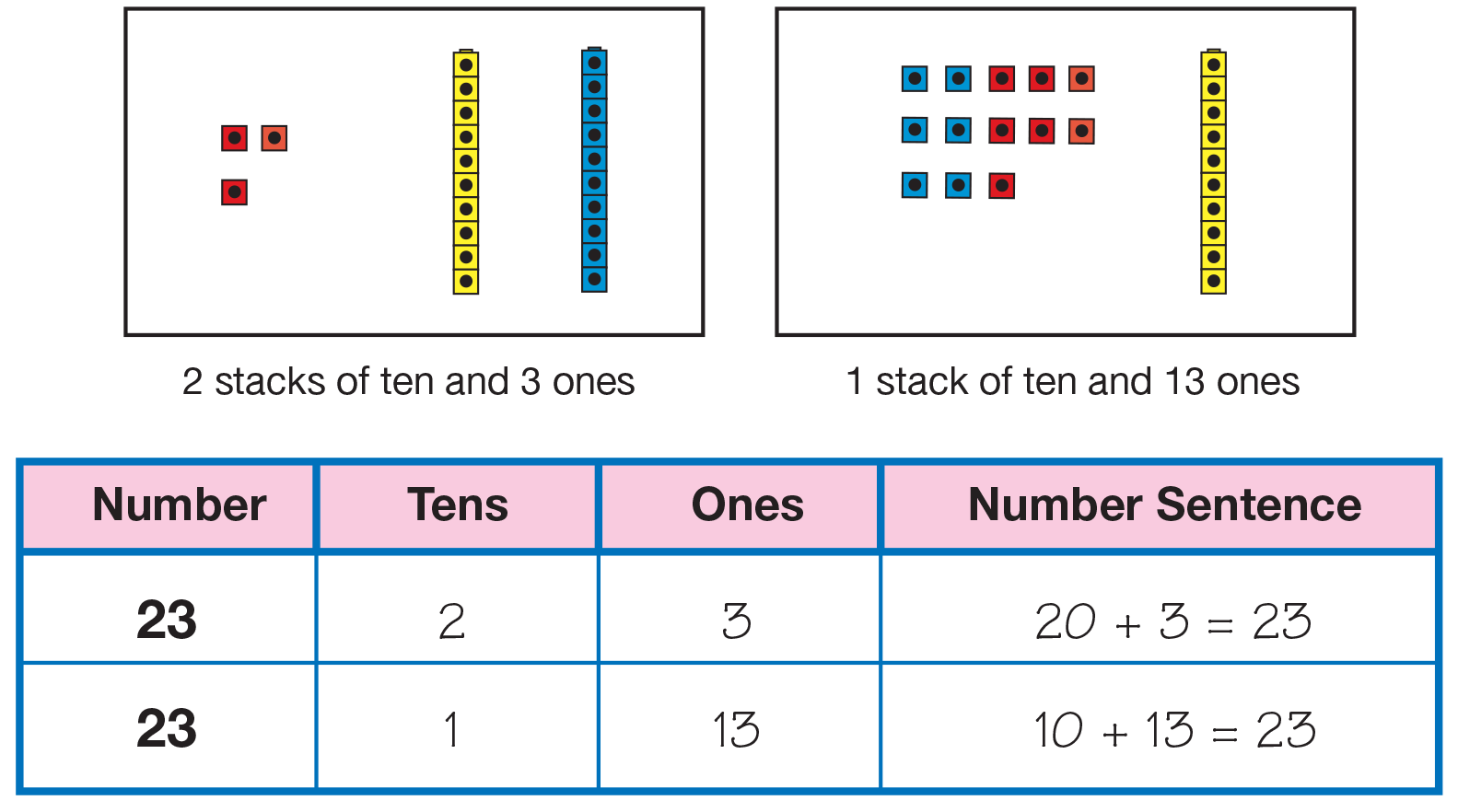
Figure 1: Students write numbers for each group in the appropriate columns and write a number sentence to show that the different partitions have the same total

Students continue to partition numbers into tens and ones in Unit 6 Place Value. In that unit, their activities lead to a recognition that the most useful partition is the one in which all trades have been made and the fewest base-ten pieces are used. This is the partition that gives the number. For example, with 6 hundreds, 4 tens, and 7 ones, all possible trades have been made; no more tens can be made from the ones and no more hundreds can be made from the tens. Therefore, the number is 647.

To be able to develop flexible and efficient methods for addition and subtraction, students must be able to compose and decompose numbers mentally. To develop visual images that will support this thinking and development of place value concepts, students represent numbers as moves of ones, tens, and hundreds on number lines as shown in Figure 2.

Figure 2: Representing 24 on a number line

During the lab Marshmallows and Containers, students explore the relationship between the shape of a container (e.g., height and width) and how much the container holds (its volume). This exercise focuses on one of the classic experiments of Jean Piaget: the conservation of volume. Piaget used three different containers. Water from one container was poured into a narrower and taller container and then into a wider and shorter container.

Piaget found that four- to six-year-olds thought that the narrow, tall container contained more water than the other two containers because as Piaget noted:

" … the water in B [the narrow container] is higher than it was in A [the first container]; therefore it increased in quantity, regardless of the fact that it is the same water that has merely been poured from one container to another."

However, by the age of 7 or 8, Piaget found that:

… the child says: "It is the same water." "It has only been poured." "Nothing has been taken away or added." "You can put the water in B [the tall container] back into A where it was before." "The water is higher but the glass is narrower, so it is the same amount."

The results of Piaget have been confirmed many times over. We found significantly older children who still confused height with volume. The lab will help some students develop a more mature understanding of the concept of volume. The data from the lab also provides a context for more practice with grouping and counting by tens and hundreds and adding and subtracting. As they did earlier with buttons, students will group marshmallows by tens, hundreds, and leftovers to facilitate development of place value concepts.

This unit begins with a lesson on time. A young child's difficulty in reading time on an analog clock may stem from an approach that focuses on both hands simultaneously but does not distinguish between how the two hands are read. "The little hand indicates broad, approximate time (nearest hour), and the big hand indicates time (minutes) after and until an hour. When we look at the hour hand, we focus on where it is pointing. With the minute hand, the focus is on the distance that it has gone around the clock or the distance yet to go for the hand to get back to the top" (Van de Walle, 2013).

In First Grade, students focus on learning to tell time with the hour hand and then add the minute hand to show times to the nearest hour and halfhour on both the analog and digital clock. In this unit, students review these concepts and recognize time to the nearest 15 minutes. They also learn to reference times as they pass through the day.

Students learn to differentiate events that happen at 4:00 am and 4:00 pm.

Students learn that the hour hand indicates the approximate time to the nearest hour, by pointing to a number between 1 and 12 on the clock face. They observe that the hour hand moves slowly from one hour to the next as the minute hand makes a complete circle and that it is in different positions as the minute hand moves. In this way, they learn to estimate and show approximate time by marking the position of the hour hand alone.

When students begin working with the minute hand, they already have a clear understanding that it is the hour hand that is the primary indicator of time. Their focus on the minute hand then becomes a question of determining how many minutes have passed since the last hour or how many minutes until the next hour. The focus is on the parts of 60, rather than the parts of 12.

This function of the minute hand is shown on students' individual clocks. The increments of 60 (counted by 5s) are shown in blue on the face of the clock, which matches the minute hand. The numbers 1–12 are in red, as is the hour hand. Students see that the numbers 1 to 12 on a clock can be used as markers for skip counting by fives to determine the number of minutes past an hour. They have no need to memorize a fact that may seem meaningless to them, such as "4 on the clock means 20 minutes past the hour."

Students will learn to tell time on an analog clock more quickly when frequent references are made to the time throughout their day and they are reminded to look at the clock. For example,

• "It's 9 o'clock, time for math."
• "You're back from art class; what time is it?"
• "In half an hour, we go to lunch. If it's 11 o'clock now, what time will we eat lunch?"

In upcoming units, students will study elapsed time using their individual clocks, again in conjunction with frequent references to the time as it passes throughout the day.

In this unit, students continue to systematically review the addition facts. Daily Practice and Problems items in this unit can be used to assess students' strategies with the addition facts in Group F (8 + 6, 9 + 6, 9 + 7, 10 + 4, 10 + 5, 10 + 6, 10 + 7, 10 + 8, 9 + 8, 9 + 9).

These facts involve the make-ten and use-ten addition strategies.

Making Ten
To solve 8 + 6 the 6 is split to make ten with the 8. 8 + 2 + 4 = 14.

Using Ten
To solve 9 + 6. I think about 10 + 6 = 16 so 9 + 6 is one less or 15.

As students develop fluency with these facts, they will be able to name the related facts in the fact family.

To be able to develop flexible and efficient methods for addition and subtraction, students must be able to compose and decompose numbers mentally. To develop visual images that will support this thinking and development of place value concepts, students represent numbers as moves of ones, tens, and hundreds on number lines as shown in Figure 2.

Resources

• Common Core State Standards Initiative (CCSSI). Common Core State Standards for Mathematics. National Governors Association Center for Best Practices and the Council of Chief State School Officers, Washington, DC, 2010.
• Fuson, K.C. "Developing Mathematical Power in Whole Number Operations." In A Research Companion to Principles and Standards for School Mathematics, pp. 68–94. J. Kilpatrick, W.G. Martin, and D. Schifter, eds. National Council of Teachers of Mathematics, Reston, VA, 2003.
• National Research Council. "Developing Proficiency with Whole Numbers." In Adding It Up: Helping Children Learn Mathematics, pp. 181–229. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
• Principles and Standards for School Mathematics. National Council of Teachers of Mathematics, Reston, VA, 2000.
• Singer, D.G., and T. Revenson. A Piaget Primer: How a Child Thinks. Plume, New York, 1996.
• Thompson, C.S., and J. Van de Walle. "A Single-Handed Approach to Time." Arithmetic Teacher, National Council of Teachers of Mathematics, Reston, VA, 1981.
• Van de Walle, J.A., K.S. Karp, and J.M. Bay-Williams. Elementary and Middle School Mathematics: Teaching Developmentally, Eighth Edition. Pearson Education, Inc., Upper Saddle River, NJ, 2013.