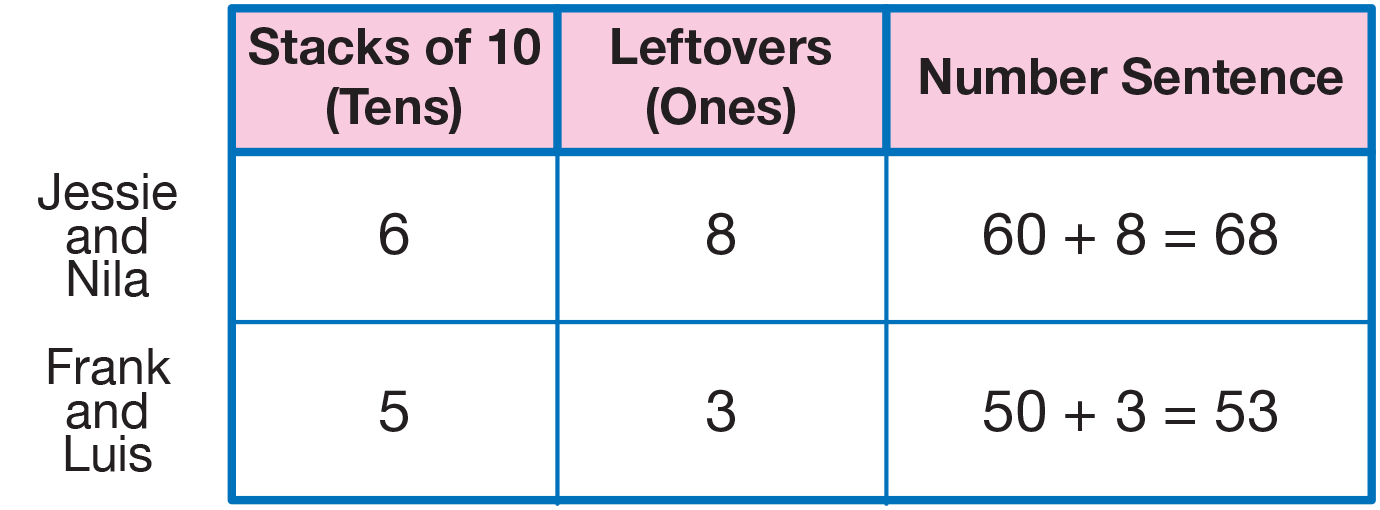
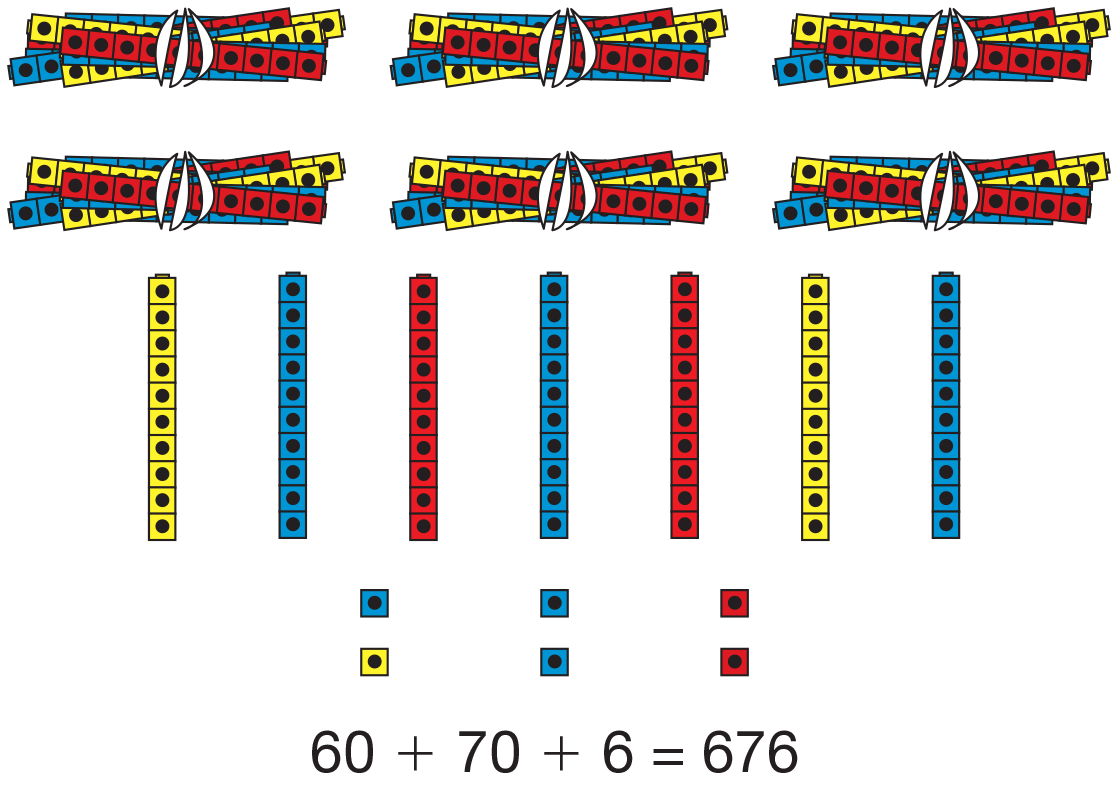
Use displays of the Professor Peabody's Problems
pages from the Student Activity Book to review representing
two- and three-digit numbers using connecting
cubes. The problems ask students to
compare the quantity of pieces after the cubes have
been grouped into bundles of hundreds, stacks of
tens, and leftovers, versus the value of the pieces.
See Content Note on connecting cubes.
Display Question 1. Here the emphasis is on the
ones.
After the problem is read aloud by one of the
students and the details of the problem are presented,
ask:
- How many total cubes is Emily showing with all
her pieces? (19)
- How many total cubes is Josh showing? (21)
- Can we compare the totals by just inspecting the
ones? Why or why not? (No, because we have to
think about the tens, too.)
- What else do we need to think about to help
Professor Peabody? (All the pieces together
make the value of the number modeled.)
Allow time for students to discuss the questions with
a partner and then write their responses.
Display Question 2. In this question, the emphasis
is on the total number of pieces.
After the problem is
read aloud and the details of the problem are presented,
ask:
- How much is Sara showing? (32)
- How much is Luis showing? (19)
- Can we count the number of pieces to compare
total values? Why or why not? (No; You have to
think about whether the pieces are in tens or
ones.)
- What should we tell Professor Peabody? (to count
the stacks by tens)
Display Question 3. In the third question, Professor
Peabody uses correct digits in his response, but the
wrong place value.
- Did Professor Peabody show 109 correctly? (no)
- What number did Professor Peabody show? (190)
- How can we correct his work? (The bundle of 100
is okay but he needs 9 cubes, not 9 stacks of ten
cubes.)
Display Question 4. In the fourth question, Professor
Peabody thinks that 40 + 5 = 50 + 4 is a true number
sentence.
- What do you know about true number sentences? (Both sides of the equation show the same
amount.)
- Is 40 + 5 = 50 + 4 a true number sentence? Show
or tell us how you decided. (No; Possible
response: There are 4 tens on one side of the
equal sign and 5 tens on the other side. There are
5 ones on one side and 4 ones on the other side.
40 plus 5 is 45 and 50 + 4 is 54. It is not a true
number sentence because the equations on each
side of the equal sign show different sums.)
Professor Peabody's problems revealed three important
aspects of place value:
- All of the pieces together make up the value of the
number modeled.
- The sum of the value of the pieces determines the value
of the number modeled.
- The order of the digits in any number is important.