Every Number Has Its Place

Est. Class Sessions: 2

Developing the Lesson

Part 2: Representing Partitions of Two- and Three-Digit Numbers

Distribute connecting cubes to student groups. The size of each student group will be determined by the number of students in the class and the number of connecting cubes. Each student group needs about 200 connecting cubes.

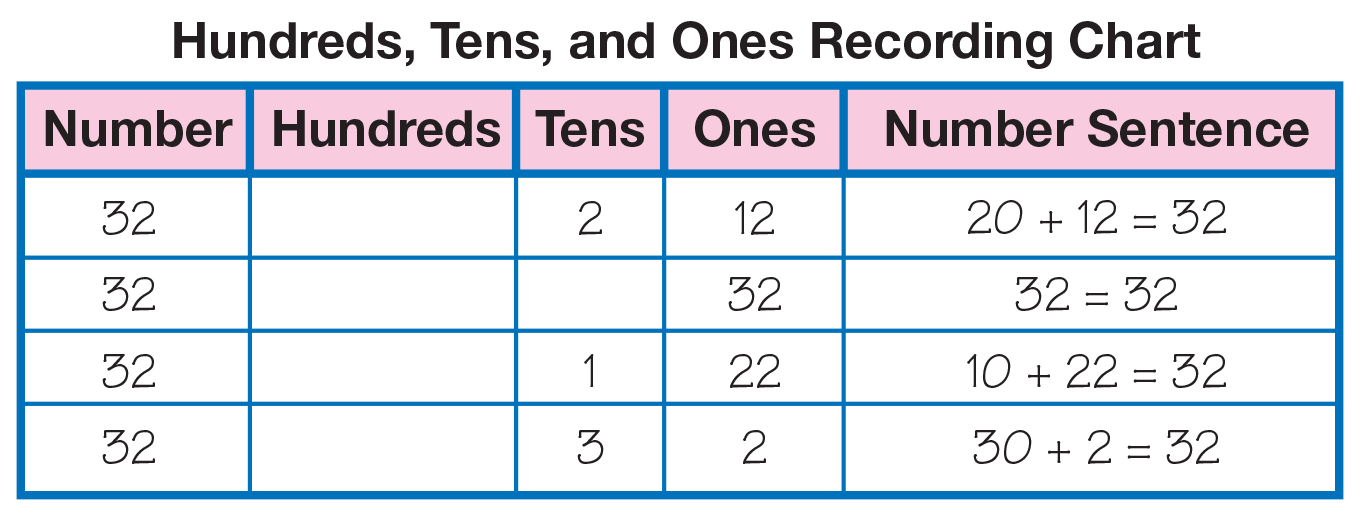
Ask students to represent 32 with the connecting cubes. Give students time to answer the following question:

How can you represent 32 by using groups of ones and tens? Find all the ways.

The following are possible combinations:

32 ones
22 ones and 1 stack of ten
12 ones and 2 stacks of ten
2 ones and 3 stacks of ten

Discuss the words ones, tens, and hundreds. Tell students that instead of using the word leftovers, they will use the word ones. Instead of using the phrase stacks of ten, they will call them tens, and instead of using bundles of hundreds, they will call them hundreds.

Display the Hundreds, Tens, and Ones Recording Chart Master. As students volunteer a representation for 32, ask students how you can write a number sentence that reflects that representation. See Figure 1 for possible ways of representing 32 and writing the matching number sentences.

Ask:

Look at the chart. What is the same about all the different partitions of this number? (They all equal 32. The different partitions of 32 all equal 32.)
Is 20 + 12 = 32 a true number sentence? How do you know? Use cubes to prove it. (Yes, both sides of the equal sign show 32. 2 stacks of ten cubes and 12 ones is 32.)
Is 3 tens and 2 ones the same as 3 ones and 2 tens? How do you know? (No; Possible response: 3 tens is 30 plus 2 ones is 2 more, 32. 3 ones and 2 tens is 3 plus 20, 23. 3 stacks of ten cubes and 2 ones is different from 3 ones and 2 stacks of ten.)
When I write 32 and 23, does the order of the digits matter? (Yes, the order of the digits is important because each place has a certain value. A digit has a certain value based on its place in the number.)

Next, ask:

What are some of the different ways to represent 145?

The following are just some of the possible combinations:

1 hundred, 4 tens, and 5 ones
145 ones
14 tens and 5 ones
13 tens and 15 ones
12 tens and 25 ones

Ask students how you can write a number sentence for each representation on the display of the Hundreds, Tens, and Ones Recording Chart Master. See Figure 2.

Ask:

How do you know [14] tens is [140]? (Possible response: I can count 14 stacks of ten by tens: 10, 20, 30 … 140.)
What does the [5] in the ones column represent? (five single cubes)
How many stacks of ten cubes make 100? (10 stacks of ten cubes each)

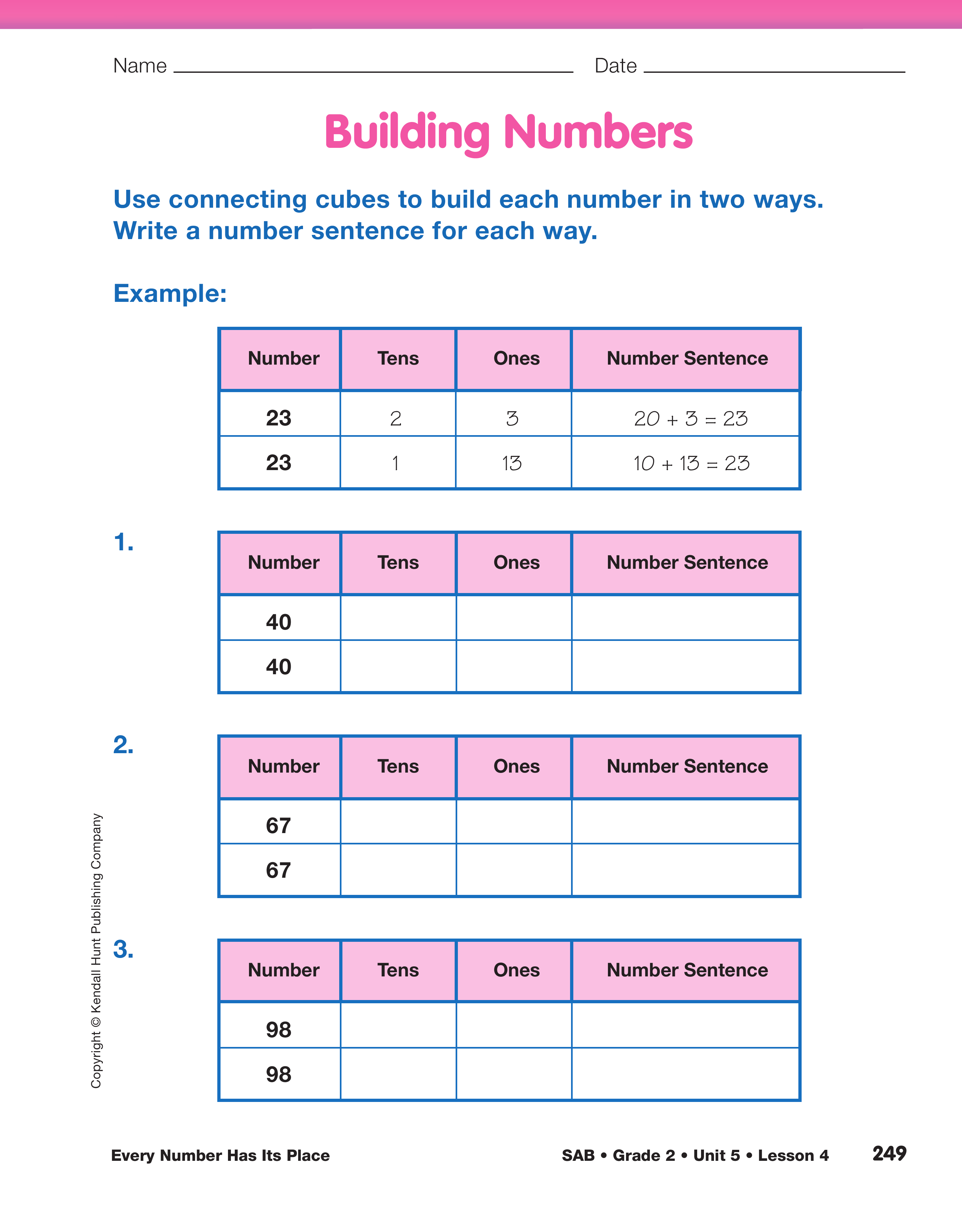
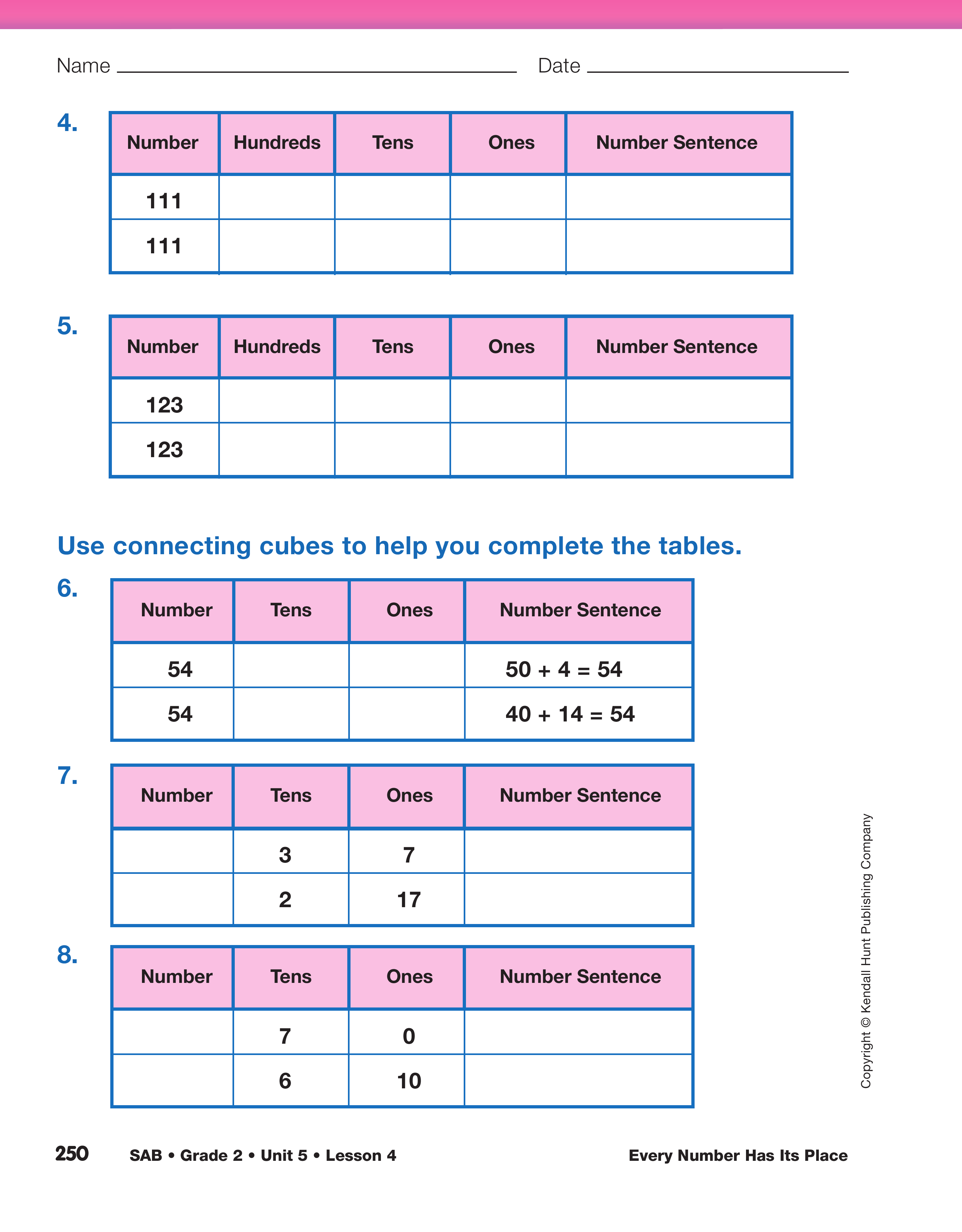
Use the Building Numbers pages in the Student Activity Book and ask students to represent the numbers 40, 67, 98, 111, and 123. In Questions 1–5 students build a number with connecting cubes, record their work, and write a number sentence to reflect the way they constructed the number. Then students are asked to build the same number in a different way, record their work, and to write a number sentence that reflects the second way they constructed the number.

After students have worked through Questions 1–5, ask a volunteer to show on the board or chart paper how he or she constructed 123 and to write the number sentence (Question 5). Ask at least two other students to show how they constructed 123 in a different way and to write their number sentences. Students should be continually encouraged to use their connecting cubes to respond to this activity.

Ask:

Does the number sentence show how 123 was built with hundreds, tens, and ones?
How are all these examples the same? (They all show 123 total cubes.)
How are all these examples different? (The groups of hundreds, tens and ones are different.)
What is another way to show 123?
How do we know that all these representations show 123? (They all show the same number of total cubes.)
Is this a true number sentence: 100 + 20 + 3 = 100 + 23? How do you know? (Possible response: I can show that 1 bundle of 100, 2 stacks of ten, and 3 more cubes is the same as 1 bundle of 100 and 23 single cubes. Both groups show the same number of total cubes. I can see that there is one hundred, 2 tens, and 3 ones on both the left side and the right side of the equal sign.)
What is another true number sentence for 123? (Possible response: 90 + 30 + 3 = 120 + 3)
Is this a true number sentence: 3 + 20 + 100 = 100 + 20 + 3? How do you know? (Yes, both sides of the equal sign show the same amount, 123.)

For Question 6, students are given the number 54 and two number sentences showing partitions of 54. They are asked to write the number of tens and ones reflected in the number sentences. Students are also given two examples in Questions 7–8 where the number of tens and ones are given, and they are asked to write a number sentence that reflects the numbers given.

Upon completion, direct students' attention to Question 7 and discuss.

Write 2 tens and 17 ones on a blank display of the Hundreds, Tens, and Ones Recording Chart Master.

Ask:

How can I build this number with my connecting cubes? (2 stacks of tens and 17 leftover ones)
What number sentence can I write that will represent this grouping? (20 + 17 = 37)
How did you know there were 37 total cubes? (Possible response: I counted on ten: 20, 30 and 7 more.)
Is there another way I can represent this number? (3 tens and 7 ones or 1 ten and 27 ones)

Try it with another number, for example, 220. Write 1 hundred, 12 tens, 0 ones on the chart. Repeat the above questions.

Then ask:

Can I write it a different way so that I have ones in my table? How might I do that? (1 hundred, 11 tens, and 10 ones)

Write a number sentence on the chart: 100 + 3 = 103.

Ask:

How might I build this number with the connecting cubes? (1 hundred and 3 ones)
What is another way to build this number? (Possible responses: 9 tens and 13 ones; 103 ones)

Adventure Book:

Student Activity Book: 249 250

Answers