Display the Cubes on Desks Master. Conclude the
lesson by telling the students number stories like you
did in Lesson 3, this time modeling numbers in the
hundreds. Ask student volunteers to assemble 10
stacks of ten cubes. Bundle the ten stacks with a rubber
band to make a model of 100.
- How many cubes are in this bundle? How do you
know? (100; Possible response: I can count the
stacks by tens. 10 tens in 100.)
Challenge students to match the number being
described in each story to the numbers modeled with
connecting cubes on Desks A, B, C, or D on the
Master. Ask them to represent the groups of hundreds,
tens, and ones in the stories on the charts on
the Master.
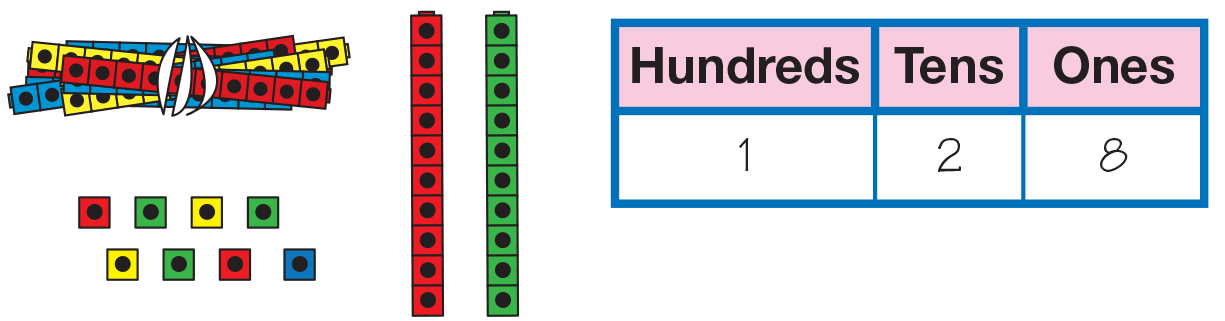
- Diana and Sam put their cubes together. They
arranged 128 cubes on Diana's desk. Which desk
has 128 cubes? (B; See Figure 3.)
- How many hundreds did they have? Tens? Ones?
Let's record that on the chart. (1 hundred, 2 tens,
and 8 ones)
- [Point to the 1 on the chart.] How many cubes
does the 1 represent? (100 cubes)
- [Point to the 2 on the chart.] How many cubes
does the 2 represent? (20 cubes)
- [Point to the 8 on the chart.] How many cubes
does the 8 represent? (8 cubes)
- How can you write this as a number sentence? (100 + 20 + 8 = 128)
Use the numbers 102 and 213 in the following stories.
213 is represented in two ways on two different
desks. After the stories, prompt students with questions
similar to the ones for the number 128 and continue
to fill in the charts and number sentences on
the Master for each number.
- Natasha and Suzanne worked with 102 cubes on
Suzanne's desk. Which desk belongs to Suzanne? (A; See Figure 4.)
- How many hundreds did they have? Tens? Ones? (1 hundred, 0 tens, and 2 ones)
- [Point to the 1 on the chart.] How many cubes
does the 1 represent? (100 cubes)
- [Point to the 0 on the chart.] How many cubes
does the 0 represent? (0 cubes)
- [Point to the 2 on the chart.] How many cubes
does the 2 represent? (2 cubes)
- How can you write this as a number sentence? (100 + 0 + 2 = 102 or 100 + 2 = 102)
- Josh and Sara put 213 cubes on Josh's desk.
Which desk has 213 cubes? (C or D)
- How can both desks show 213 cubes? (Desk C
has 1 hundred, 11 tens, and 3 ones and Desk D
has 2 hundreds, 1 ten, and 3 ones.)
- What is a number sentence that describes the
cubes on Desk C? (100 + 110 + 3)
- What is a number sentence that describes the
cubes on Desk D? (200 + 10 + 3)
- Is this a true number sentence: 100 + 110 + 3 = 200 + 10 + 3? How do you know? (Yes, both
sides of the equal sign show 213.)
- Let's put all our cubes together and build models
to show that this number sentence is true.
Assign the Putting Together and Taking Apart
Assessment Master for students to complete individually.
Each student will need access to 50 connecting
cubes.
Use the Putting Together and Taking Apart Assessment
Master with the Feedback Box to assess students' abilities to
represent quantities using connecting cubes and symbols
[E1]; compose and decompose numbers using ones, tens,
and hundreds [E2]; show different partitions of numbers
using connecting cubes and number sentences [E3]; read
and write numbers [E5]; make connections between place
value concepts and representations of numbers with
connecting cubes and number sentences [E6]; recognize that
different partitions of a number have the same total [E7]; and
show work [MPE5].
Use the Worskshop in Lesson 6 to provide targeted practice
with these Expectations.