Display a blank Tens and Ones Recording Chart
Master. You will use this to record students'
responses. See Figure 3. Have students work in
groups of 2–4 with about 100 connecting cubes per
group. Tell a number story
For example, write the
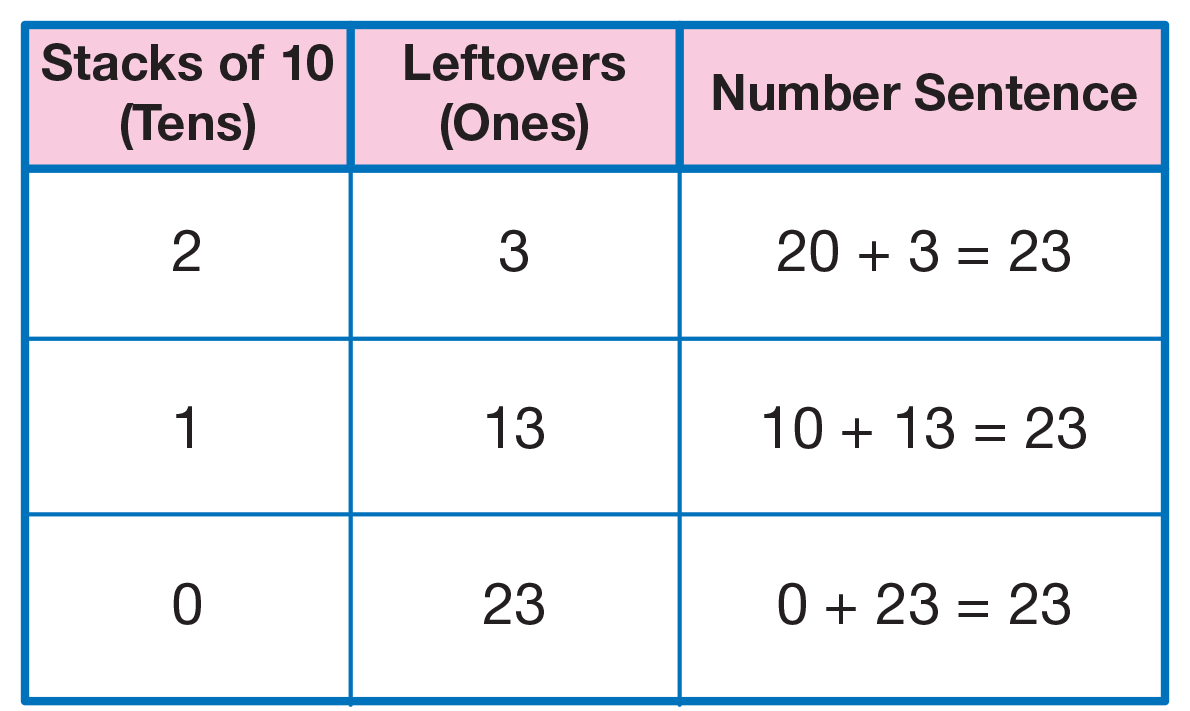
number 23 on a display and say:
- Luis had 23 cubes from the class collection. Make
a model of Luis' connecting cubes with your connecting
cubes using stacks of ten.
- How many stacks of ten in 23? (2 stacks of ten;
See Figure 3.)
- How many leftovers? (3 leftovers)
- [Point to the 2 in 23] How many cubes does the
2 represent? (20 cubes) How do you know? (2 stacks of 10 is 20.)
- [Point to the 3 in 23] How many cubes does the
number 3 represent? (3 cubes)
- How can we write our stacks of tens and our leftover
ones as a number sentence? (20 + 3 = 23)
- Can you represent the number 23 a different way,
using only tens and ones? (10 + 13 = 23)
For students who need more of a challenge, ask them to
model a three-digit number with connecting cubes. Students
should describe the number as you point to digits or piles of
connecting cubes.
If students need further prompting, ask:
- What if you had only one stack of ten?
- How many leftovers would you have then? (1 stack of ten, 13 leftovers)
- Would that still be 23 cubes? Show how you know. (It is still 23 cubes because 1 can count the
cubes, 10, 11, 12, 13 … 20, 21, 22, 23.)
- What is a number sentence that describes this
representation? (10 + 13 = 23)
To help students recognize that different partitions of
a number have the same total, display the number
sentence 20 + 3 = 10 + 13 and ask:
- Is this a true number sentence:
20 + 3 = 10 + 13? How do you know? (Yes,
because both sides of the equal sign show the
same amount, 23.)
- How can you use cubes to show that this is a true
number sentence? (I can build a tower of
20 cubes and 3 cubes, and another tower of 10
and 13 and compare them. They are the same
height so 20 + 3 = 10 + 13.)
- Is there another way to represent the number 23
using only tens and ones? What if you had zero
stacks of ten? How many leftovers would you have
then? (23 leftovers)
- What is this number sentence? (0 + 23 = 23)
- Is 0 + 23 = 10 + 13? How do you know? (Possible response: Yes, because 0 + 23 is 23
and 10 + 13 is also 23.)
Give students other 2-digit numbers to model with
their cubes, keeping the numbers below 40. Ask students
to model each number with different combinations
of tens and ones and write number sentences to
describe each way of partitioning. For each new
number, display a new chart and have students fill it
in as they did for 23.
Reverse your number stories and challenge students
to tell you the number.
- Grace had 2 stacks of ten and 7 leftovers. How
many cubes did Grace have? What is a number
sentence to describe Grace's cubes? (27; 20 + 7 = 27)
- Romesh showed the same number as Grace did
but in a different way. Show how Romesh could
have grouped his cubes. (10 + 17 = 27 or
0 + 27 = 27)
Continue to tell stories and encourage students to
make up their own to challenge the class.
To provide more practice with partitioning, assign
the Tens and Ones pages in the Student Activity
Book. Tell students this practice will prepare them
for the game to be played later in the lesson.
When students have completed the Tens and Ones
pages, ask them to consider the number sentences
from Check-In: Question 4.
Display the following
number sentences and ask:
- Is 20 + 21 = 10 + 31? How do you know? (Possible response: Yes. I can put 20 and 21
cubes together and the tower is just as tall as a
tower of 10 and 31 cubes put together.)
- Is 12 + 20 = 20 + 21? How do you know? (Possible response: No, 12 + 20 is 32 and
20 + 21 is 41.)
- Is 30 + 11 = 40 + 1? How do you know? (Possible response: Yes, because both sides of the
equation show 41.)

Use Check-In: Question 4 on the Tens and Ones pages in the
Student Activity Book to assess student's abilities to
represent quantities using connecting cubes and number
sentences [E1]; decompose numbers using ones and tens
[E2]; show different partitions of numbers using connecting
cubes and number sentences [E3]; and read and write
numbers [E5].
To provide targeted practice with grouping by tens, students
can play the Fifty Wins Game. Provide copies of the Masters
with the directions, spinner, and the Fifty Wins Game Board.
Place them in a center along with a clear plastic spinner, or
pencils and paper clips, and fifty connecting cubes per player.
In addition, students can use the Not More Than 100 Game
pages from the Student Activity Book to practice
decomposing numbers into tens and ones and partitioning.
Provide copies of the pages, including the spinner and
recording sheets, spinner materials, 200 Charts, and
100 connecting cubes grouped in tens and ones for each
player.

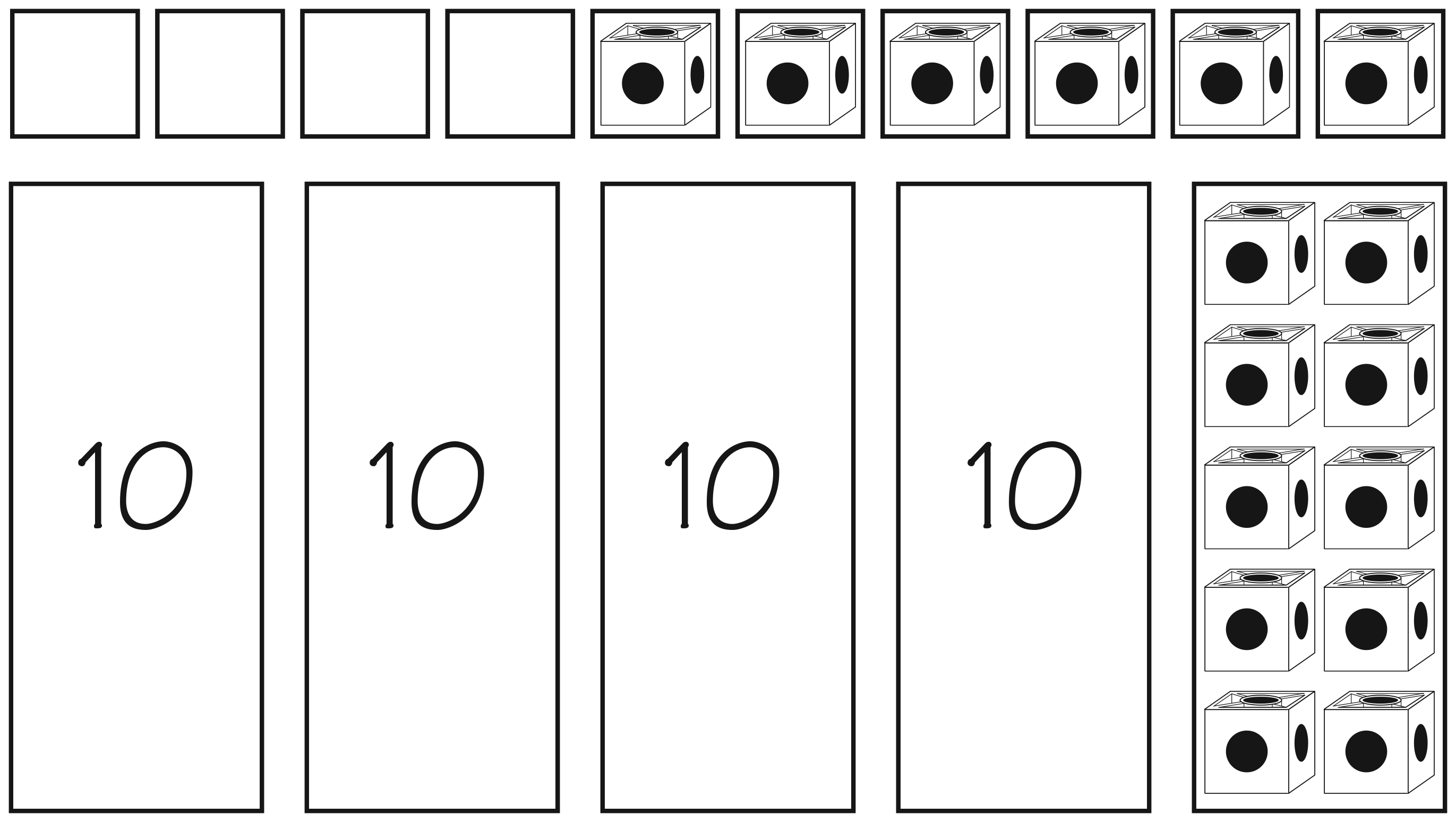
Students who are still reluctant to group by tens or who need
more practice can play an alternate game on the Fifty Wins Game Master. In this game, they practice grouping by tens.
Each student has his or her own game board. Students spin a
spinner to determine if they win or lose 1 or 10 connecting
cubes. Individual connecting cubes can only be added or
taken away from the small boxes. When all ten small boxes
are filled, students move the ten cubes to a big box. The goal
is to have all 5 big boxes filled with 10 cubes each.
Students should play the game for 2 or 3 rounds.
See Figure 4.