Mathematics in this UnitPrint

Grouping and Counting

Developing Number Sence

In this unit, students group and count objects. They skip count by twos, fives, and tens. This experience strengthens students’ number sense so they can use a range of numbers in future units to explore measurement, place value concepts, addition, subtraction, and computation. … read more

X

Developing Number Sence

In this unit, students group and count objects. They skip count by twos, fives, and tens. This experience strengthens students’ number sense so they can use a range of numbers in future units to explore measurement, place value concepts, addition, subtraction, and computation.

Students count by twos by counting hands, arms, and other objects that are naturally grouped by twos. Counting by fives occurs in the context of counting fingers on one hand, grouping pennies by fives, and substituting a nickel for every group of five pennies. After grouping pennies by fives, students count on to then find the value of a set of coins. See Figure 1. Counting by tens is motivated by counting fingers on both hands and grouping objects in tens with ten frames.



Figure 1: Counting 13 pennies by skip counting by fives and counting on

Students will also describe and name numbers in terms of groups. It is important for students to think about groups of numbers. Work with 12, for example, includes far more than the fact that it is twelve ones or the number that comes after eleven. Twelve is also two 6s, three 4s, and two 5s with 2 left over. See Figure 2.



Figure 2: 2 groups of 5 with 2 left over

Finding the number of a collection of objects by grouping and counting by tens and counting leftovers is an early step in students' development of number sense for the value of two-digit numbers.

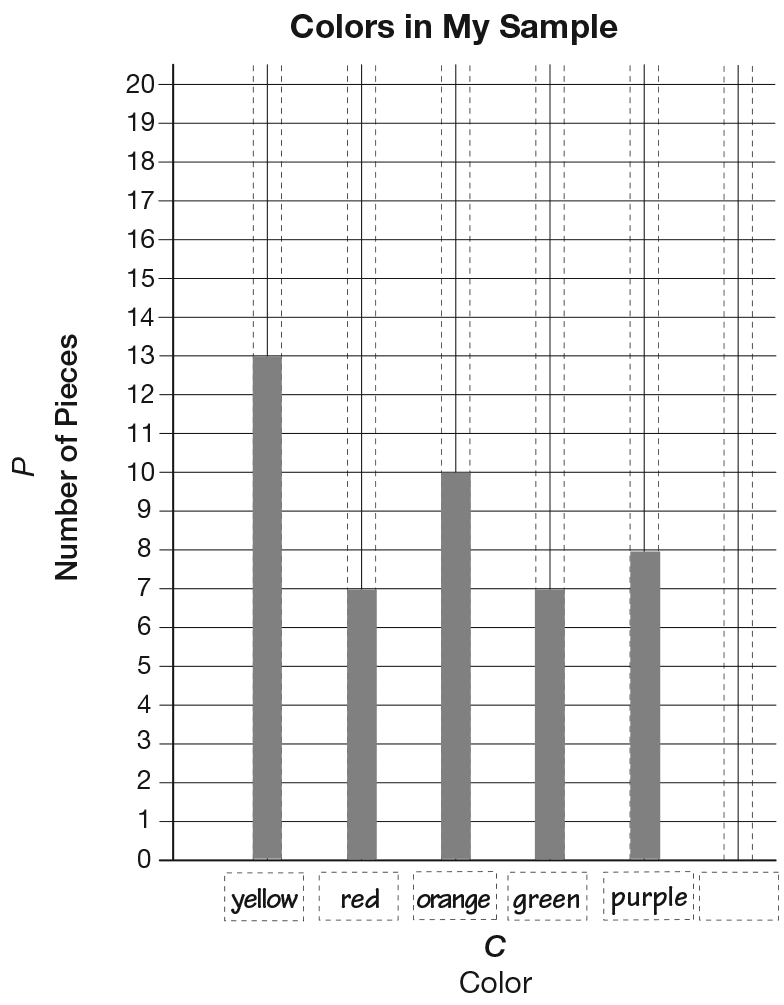
In Lessons 3 and 5, students group and count objects by ten to develop their ideas of “ten-ness.” They group and count objects in various contexts such as number of fingers, money, packing cookies in boxes of ten, and counting the colors of cereal pieces in a box. See Figure 3. Students use different representations to group and count objects by ten, including number lines, ten frames, and graphs. All the activities contribute to students' notions of the size of numbers and the usefulness of thinking in tens. Making connections among the representations will strengthen students' understanding of these important ideas.



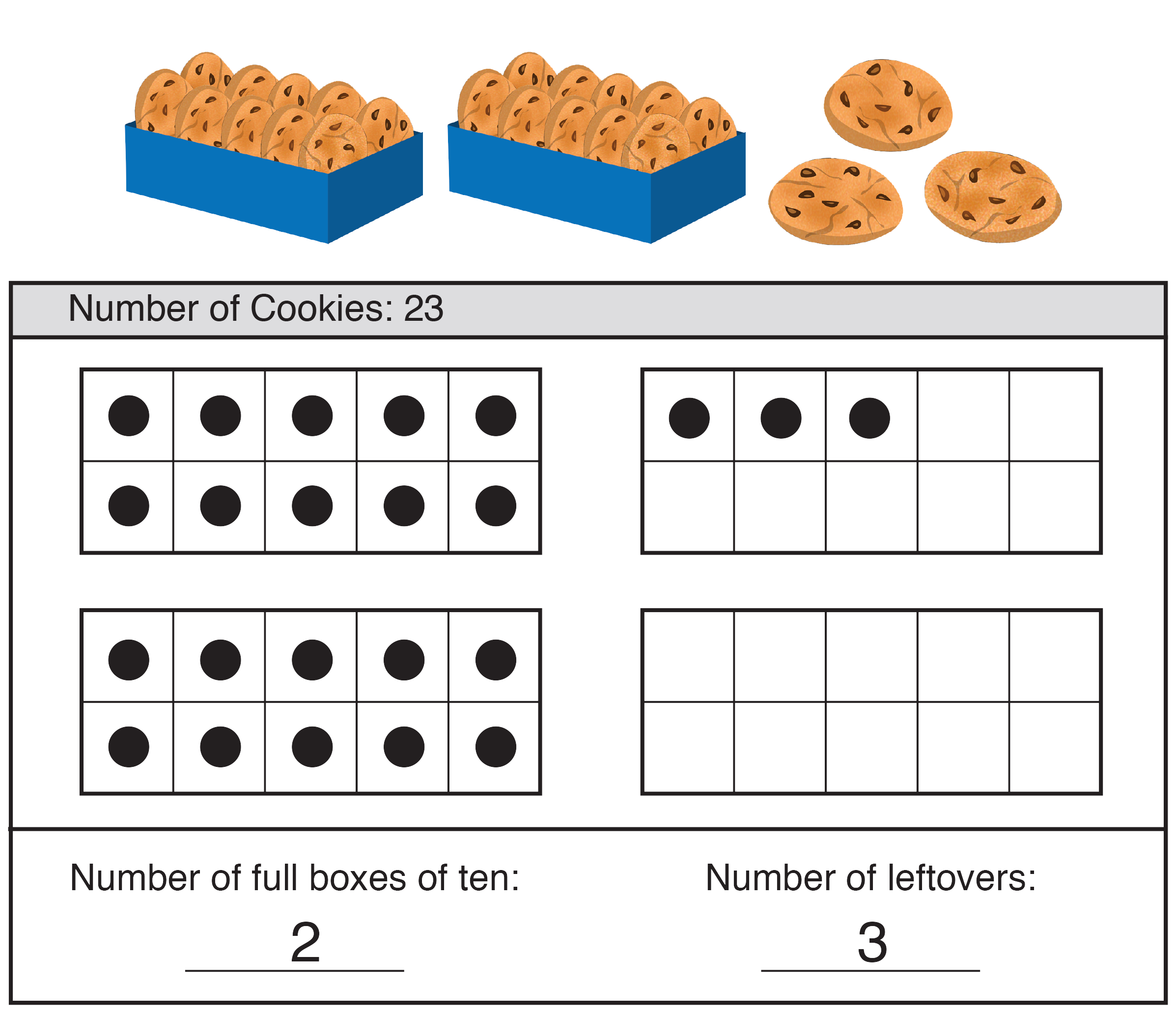
Figure 3: Partitioning a collection of objects into groups of tens and leftovers (ones)

Introducing the TIMS Laboratory Method

“Quantitative reasoning entails habits of creating a coherent representation of the problem at hand; considering the units involved, attending to the meaning of quantities … ” (Common Core State Standards Initiative, 2010). … read more

X

Introducing the TIMS Laboratory Method

“Quantitative reasoning entails habits of creating a coherent representation of the problem at hand; considering the units involved, attending to the meaning of quantities … ” (Common Core State Standards Initiative, 2010).

Students will apply their grouping and skip-counting experiences in the Colors laboratory investigation. In the lab, students explore sorting and sampling. Through this activity and others like it, students begin to understand what can be said about a collection by looking at a sample. The investigation provides an example of sampling techniques that are used by scientists, business people, and others who regularly analyze data.

Students are in the process of developing facility with different problem-solving tools, such as graphs, tables, manipulatives, diagrams, and calculators. With Colors, some of these tools are combined into a process similar to one used regularly by scientists—the scientific method. Students portray a problem situation using a picture. They collect data, organize it in a data table, and graph it. See Figure 4. Then they use tools to look for patterns and analyze the data carefully. This simplified version of the scientific method is characteristic of TIMS laboratory investigations. It is a powerful way to examine many different problems.


Figure 4: Graphing color data for analysis

Resources … read more
X

Resources

  • Baroody, A.J. “Why Children Have Difficulties Mastering the Basic Number Combinations and How to Help Them.” Teaching Children Mathematics, 13 (1), pp. 22–31, 2006.
  • Common Core State Standards Initiative (CCSSI). Common Core State Standards for Mathematics. National Governors Association Center for Best Practices and the Council of Chief State School Officers, D.C., 2010.
  • Goldberg, Howard, and F. David Boulanger. “Science for Elementary School Teachers: A Quantitative Approach.” American Journal of Physics, 49 (2), pp. 120–124, 1981.
  • Goldberg, Howard, and Philip Wagreich. “A Model Integrated Mathematics and Science Program for the Elementary School.” International Journal of Educational Research, 14 (2), pp. 193–214, 1990.
  • Isaacs, Andrew C., and Catherine Randall Kelso. “Pictures, Tables, Graphs, and Questions: Statistical Processes.” Teaching Children Mathematics, 2 (6), pp. 340–345, 1996.
  • Isaacs, Andrew C., Philip Wagreich, and Martin Gartzman. “The Quest for Integration: School Mathematics and Science.” American Journal of Education, 106 (1), pp. 179–206, 1997.
  • Kaput, J.J. “What Is Algebra? What Is Algebraic Reasoning?” In Algebra in the Early Grades. J. Kaput, D. Carraher, M. Blanton, eds. Lawrence Erlbaum Associates, New York, NY, 2008.
  • Smith, John P., III, and P. Thompson. “Quantitative Reasoning and the Development of Algebraic Reasoning.” Algebra in the Early Grades. J. Kaput, D. Carraher, M. Blanton, eds. Lawrence Erlbaum Associates, New York, NY, 2008.