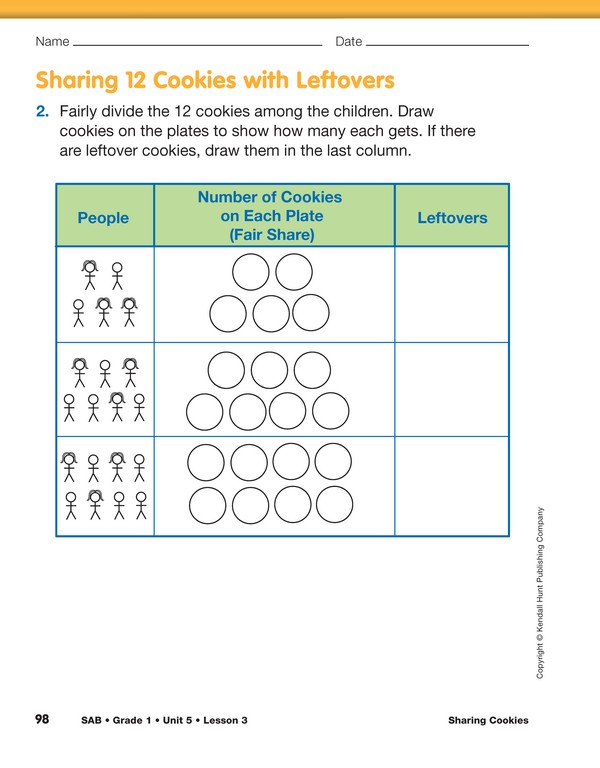
Share 12 Cookies with Leftovers.
After students
explore partitioning twelve, give them experience with
the concept of leftovers. Explain to students that when
sharing fairly, sometimes there are extras or leftovers.
Continue sharing 12 cookies with other numbers of
people as in Question 2 on the Sharing 12 Cookies
page. Ask student pairs to use their 12 counters to
solve the first problem on the page and then select students
to demonstrate their answer on the display of
Question 2.
- What is different about your answer to this problem
compared to the answers in Question 1? (There are
leftovers when we divide the cookies in this problem.
There were no leftovers in the problems in
Question 1.)
- What should we do with the leftovers? (Answers
will vary. Possible response: We can’t give them
away because there aren’t enough for everyone to
get another one. It wouldn’t be fair shares.)
Some students may suggest breaking cookies into
pieces in order to share the leftovers but encourage
them to instead indicate the leftovers in the last column.
See the Sample Dialog for an example of a class
discussion about partitioning the number twelve into
five groups.

Use this dialog to discuss partitioning twelve cookies into five groups.
Teacher: In the story, two, four, six, and twelve children
came to the door and the children were able to divide
the cookies evenly. If there were five children, how
would they divide twelve cookies? Decide how many
plates you need to represent the number of children and use the 12 counters to represent the cookies. Pass out one
cookie at a time until you run out and everyone gets a
fair share.
Melinda: I would give two children three cookies and give the
other three two cookies each.
Teacher: What does everyone else think?
Pablo: I don’t think that’s fair because I wouldn’t like it if I got
only two cookies and some children got three cookies.
Teacher: Does someone have a different answer?
Daniel: I put the 12 cookies into five groups and each child
would get two cookies, but I had 2 left.
Teacher: That’s great, Daniel! Can you show us how you got
the answer? We say that everyone received a fair share
when everybody gets the same number. We can only
give two to each person if they receive a fair share and
there are two cookies left over.
Mariela: Why can’t we break the leftover cookies into
five pieces?
Teacher: Class, what do you think about breaking the leftover
cookies into five pieces that are the same size?
Aaron: It would be too hard to break each cookie into
five even pieces. It’s better to say we have two left over.
Teacher: Good answer, Aaron! In this case, it’s better to say
we have leftovers. Now, let’s show each person’s fair
share by drawing the number of cookies each person
will get on the plates and the leftovers under the
“Leftovers” column.
Continue with other numbers shown in Question 2 so
that students will see the effect of partitioning numbers
that have leftovers. Each time students work through a
sharing situation, they record their results on the plates
in the table. Explain to students that sometimes there
are leftovers and sometimes there are no leftovers. It
just depends on how many people are sharing.
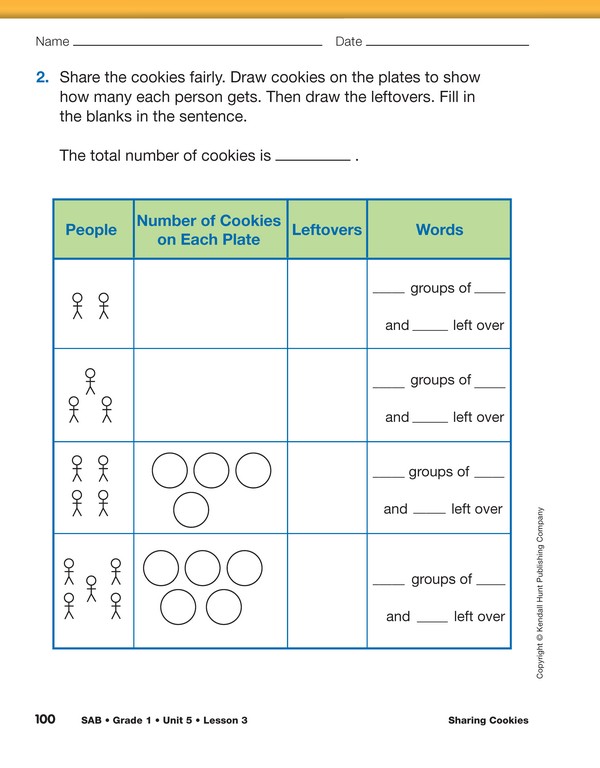
Fair Shares with 15 Cookies. Students will explore
the effects of sharing a fixed number of cookies among
different numbers of people. Display the first page of
Fair Shares (Question 1) and pass out more counters
so that each student pair has fifteen.
Discuss sharing 15 cookies with 2 people:
- There are 2 people and 15 cookies. Who can draw
the number of people under the “People” column?
- How many plates should we draw under the
“Number of Cookies on Each Plate” column? (2)
How did you decide how many to draw? (The number
of plates is the same as the number of people.)
- How many counters do we need? (15)
- Now use your counters to figure out how many
cookies each child should get. (7 cookies with
1 left over)
After students solve the problem, select a student pair
to share their problem on the display by drawing the
number of cookies each person will receive for their
fair share inside the plates and drawing the leftovers in
the “Leftovers” column. See Figure 2 for an example.
Direct students to look at the open statement, “___
groups of ____ and ____left over.”
Ask the following questions as you complete this statement:
- How many plates are there? (2)
- How many groups of cookies are there? (2)
- How many cookies are on each plate? (7)
- How many leftover cookies are there?(1)
- Who would like to complete the statement?
(2 groups of 7 and 1 left over)
After completing the example together as a class,
explain that you will write the number of people on the
top of their page and they will use their counters to figure
out the number of cookies each person will
receive. Assign quantities of 1 to 10 to pairs. Have student
pairs solve their problem and record their solution
on the page.
Upon completion of Question 1, ask:
- You all had 15 cookies to share, but you had different
numbers of people to share them with. Did
everyone share the cookies fairly? (yes)
- Did anyone have leftovers? (Answers will vary.
Some student pairs will have leftovers and some
will not.)
Select a student pair that did not have leftovers and a
pair that did have leftovers and have them show their
solutions.
- When do you have leftovers? (Possible response:
When everyone has a fair share, but there are extra
cookies left over. There are not enough leftovers
for everyone to get another one and keep it fair.)
- After sharing cookies, what if there are 3 children
and 5 leftover cookies? Does that make sense?
(That”s not right. There are too many leftovers.
Each child could have another cookie.)
Practice Fair Shares. Students will continue to practice
dividing the same number of cookies among different
numbers of people but will use a slightly
different recording process. Use a display of Question
2 on the second page of Fair Shares to illustrate how
to share 11 cookies with two children. Each student
pair will need 20 counters and 5 small paper plates.
Guide students by asking:
- How many cookies are there? (eleven)
- How many people are in the first group? (two)
- How many plates are needed in the second column?
(two; The number of plates represents the number
of children.)
- How many paper plates will you need? (2)
- Use your counters to figure out how many cookies
each person will get. Be ready to show each person’s
fair share and whether or not there are leftovers.
The leftovers should be off of the plates.
Sometimes you will have leftovers and other times
you will not, depending on the number of people
who have to share the cookies.
Select a student pair to share their solution and draw
the number of cookies each child will receive on the
displayed plates and the leftovers in the “Leftovers”
column on the display of the Fair Shares page.
- How many cookies are on each plate? (5)
- How many leftover cookies are there? (1)
- Complete the statement: ____ groups of ____ and
____ left over. (2 groups of 5 and 1 left over.)
- How did you know what to put in each blank?
(Possible response: I knew there were 2 groups
because there were 2 plates. There were groups of
5 because that is how many cookies were on each
plate. I had 1 cookie left over.)
Assign Questions 2–3 on the Fair Shares page.
Students are now ready to try problems with a different
number of cookies. Give each pair of students a
number between twelve and twenty. This number represents
the number of cookies to share, and it should
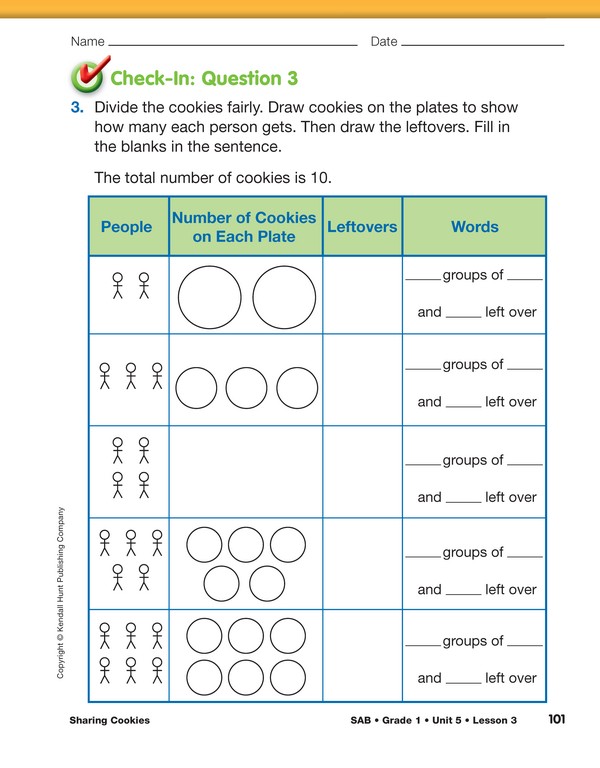
be written at the top of their page. In Check-In:
Question 3, all students will divide ten cookies fairly.
Direct students to use their counters and remind them
to place leftover cookies in the “Leftovers” column
and not on the plates.

Use Check-In: Question 3 on the Fair Shares pages with the
Feedback Box in the Student Activity Book to assess
students’ abilities to partition ten cookies into groups of a
given size and count the leftovers.
The question assesses students’ abilities to read and write
numbers to 20 [E3]; represent and identify numbers using
counters and pictures [E4]; connect representations of
quantities (counters and symbols) [E5]; and divide a
collection of objects into groups of a given size and count the
leftovers [E6]. This page can also be used to assess
students’ abilities to show their work [MPE5] and use labels
by completing the open statements [MPE6].
For targeted practice, place several copies of the first page
of Fair Shares (Question 1) in a learning center with
20 counters and two containers. One container will have the
label “Number of People” and pieces of paper with numbers
between two and six. The other container will have the label
“Number of Cookies” and pieces of paper with numbers
between twelve and twenty. (See Materials Preparation.)
Students will select one number from each container, draw
the number of people, and then use the counters to
determine each person’s fair share and leftovers, if there are
any.