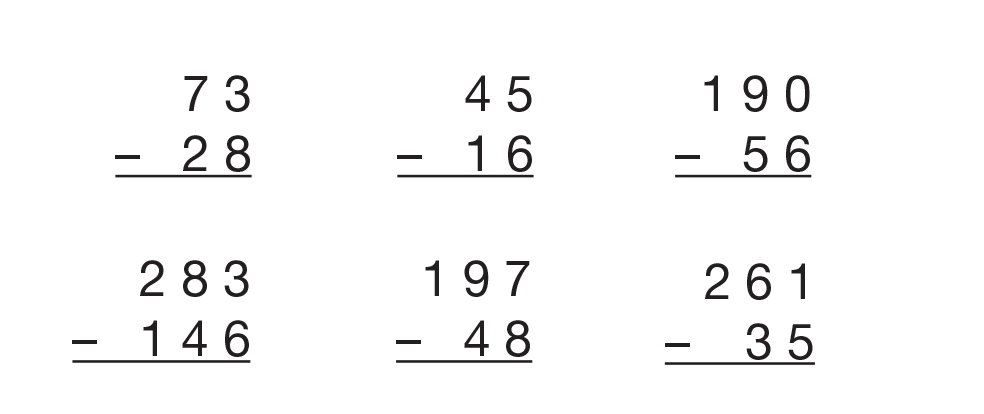Lesson 4

Subtraction with Base-Ten Pieces

Est. Class Sessions: 2

Developing the Lesson

Part 2: Subtraction Problems with Trades

Continue the activity by asking students to represent 57 with base-ten pieces. To help students think in terms of regrouping, list the various ways students can decompose 57, and include number sentences. For example:

5 skinnies + 7 bits (50 + 7 = 57)
4 skinnies + 17 bits (40 + 17 = 57)
3 skinnies + 27 bits (30 + 27 = 57), etc.

Ask:

X
  • Do all of these representations show 57? (yes)
  • Does 50 + 7 = 40 + 17? How do you know? (Yes, both sides of the equation show 57.)

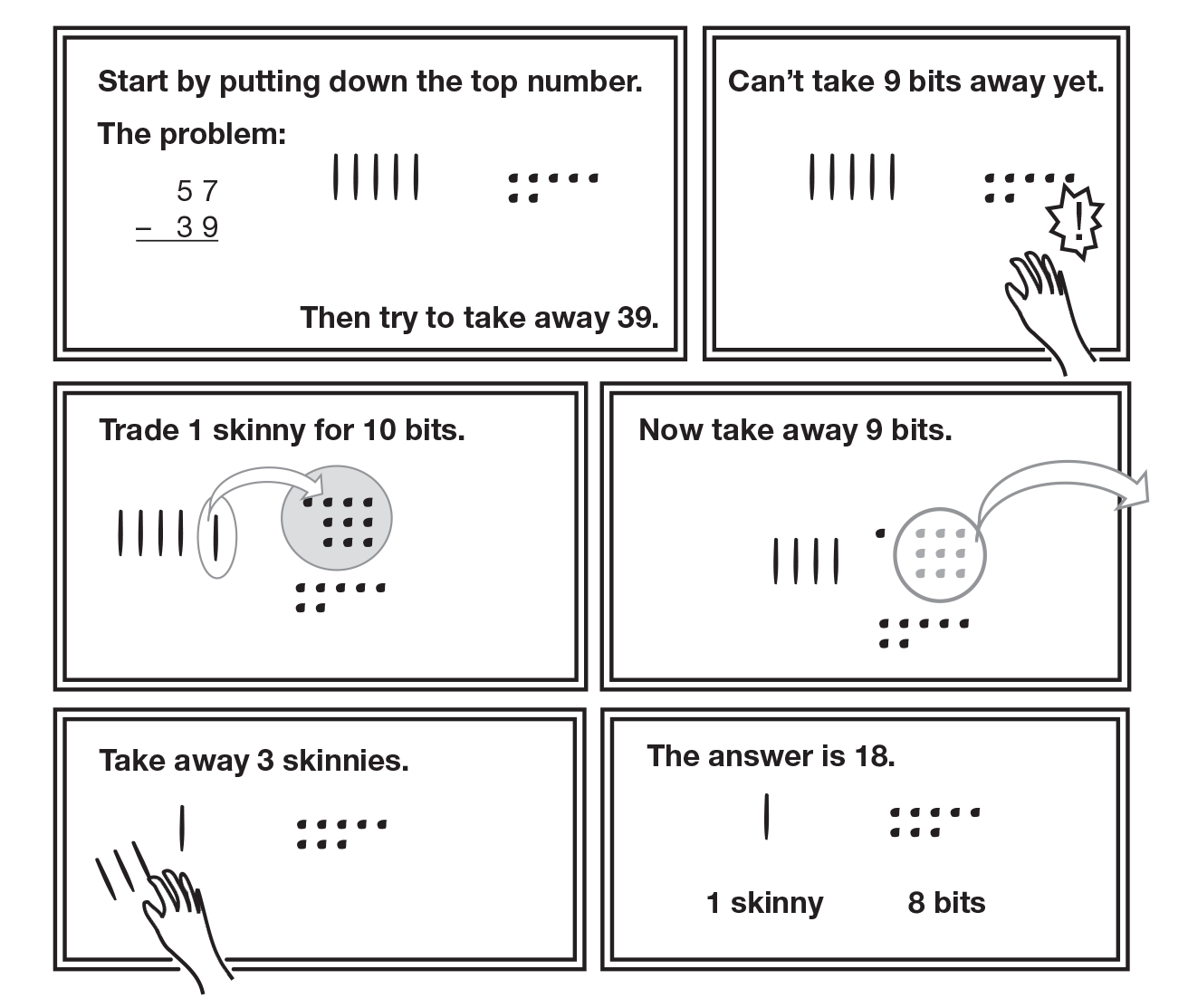
Ask students to show the number 57 with their base-ten pieces. Tell them that they will be subtracting 39 and ask them first to estimate an approximate answer.

Write the subtraction problem on the board and ask students to solve it using their base-ten pieces. Tell them they can talk with their neighbor about solving it. Give them a few minutes to work on the problem. Circulate and observe how students are dealing with the need to subtract 9 bits from 7 bits. The problem is shown in Figure 2.

Ask:

X
  • What is different about this problem? Why? (We only have 7 bits and we are supposed to take away 9.)
  • Is 57 more than 39? (yes) So, if 57 is more than 39, we should be able to take away 39. Do you agree?
  • Who has an idea for how we can do that?

If no one suggests trading one skinny for ten bits, ask probing questions like:

X
  • Could we take some bits, or ones, from our skinnies? How could we do that? (We could trade one skinny for 10 bits.)
  • How many bits does one skinny represent? (10 bits)
  • If we trade one skinny for ten bits, how many skinnies do we have now? (4) How many bits? (17)
X

Starting on the Right or Left. Subtraction using some paper-and-pencil algorithms is done from right to left—first the ones column, then the tens column. However, the subtraction in this lesson and the next—using base-ten pieces and expanded form—can be done in any order.

Because we read from left to right, students naturally tend to start solving problems on the left. For some methods—such as using mental math to subtract tens and ones—starting on the left is reasonable. As students use base-ten pieces in this lesson, they should be allowed to choose whether they subtract the ones first or the tens first.

X

Regrouping. Allow students to make trades in any way that makes sense to them. At this point, they may trade inefficiently, for example trading all their tens for ones instead of just one ten for the ten ones that they need. It is important for students to look at the amount that they have, understand that they need to find partitions of that number, and then take some away. Students must see inefficiency before they can develop efficiency. The goal in this lesson is simply exploration, not efficiency.

Have a student volunteer model the number with base-ten pieces and show the trade with the display pieces.

Ask:

X
  • Is 5 skinnies and 7 bits the same as 4 skinnies and 17 bits? (Yes, they both show 57, just in different ways.)
  • Does 50 + 7 = 40 + 17? (yes)

Ask:

X
  • Now can you subtract? What do you subtract?
    (3 skinnies and 9 bits)
  • How many skinnies and bits are left after you take away 3 skinnies and 9 bits? (1 skinny and 8 bits)
  • Can you say that in tens and ones? (1 ten and 8 ones)
  • What number is that? (18)

Provide several more problems that involve trading once, such as the problems in Figure 3. With each problem, ask the class to estimate the difference. Then ask a student to display and solve the problem, modeling the minuend (first number), making a trade as necessary, and then taking away the subtrahend (second number). Occasionally, ask students to add their answer to the amount taken away to see if they get the number they started with. Have them write number sentences.

Check for Understanding of Trading. Make sure students understand that trading does not change the number. It just changes the way it is partitioned. See Sample Dialog 2.

X
This sample dialog was taken from a classroom video. A student solves 57 − 39 and the teacher reinforces concepts about trading.

Teacher: So it's 57 minus 39. Okay, who thinks they can come up and explain to us how you're going to solve this? What are you going to do to get the right answer? John, come on up. Watch what he's doing. If he needs help you need to help him.

John: I made 57.

Teacher: How did you make 57?

John: By 5 skinnies and 7 bits.

Teacher: Can you count the 5 skinnies for us?

John: 1, 2, 3, 4, 5. [points to skinnies].

Teacher: Can you count by tens?

John: 10, 20, 30, 40, 50.

Teacher: Very good.

John: And then I, um, I can't take away 9 from 7 because I have, I don't have enough so I take away one skinny and trade it for ten.

Teacher: Ten what?

John: Bits.

Teacher: Ten bits, right. Then how many bits do you have? Can you count them out loud for us, John?

John: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17.

Teacher: This is the question I kept asking people at Table 1. After everyone at Table 1 traded their skinny for ten bits, I asked them, do you still have 57? What do you think? Do you still have 57?

Students: [Some say “No,” some say “Yes.”]

Teacher: Raise your hand if you think yes, you have 57. John, you think yes?

John: Yes.

Teacher: Prove to us that you still have the number 57.

John: Because, because you have 4 skinnies and
17 bits—that's 57. So it doesn't change.

Teacher: 57. Very good. You still have 57. See how the number doesn't change?

Lily: So that's the answer—57?

Teacher: No, he's just showing us 57. Now he has to subtract 39. So what do you do?

John: 1, 2, 3, 4, 5, 6, 7, 8, 9 [counts up nine bits and pushes them off to the side] and then I take away 3 [referring to the 3 skinnies, which he puts to the side]. That leaves
1 skinny and 8 bits [counts the bits]. That's 18.

Teacher: And it equals 18. Very good, John. Good job. How many of you got 18?

The third problem shown in Figure 3, 190 − 56, involves a zero in the ones place.

Ask:

X
  • Can you subtract 6 bits from 0 bits? (no)
  • Can you trade a skinny for 10 bits? (yes)
  • Now what pieces do I have? (1 flat, 8 skinnies, and
    10 bits)
  • How do we finish this problem now? What do we subtract? (Take away 5 skinnies from the 8 skinnies; take away 6 bits from the 10 bits.)
  • What do we have left? (1 flat, 3 skinnies, and 4 bits)
  • Can you say that in hundreds, tens and ones?
    (1 hundred, 3 tens, and 4 ones)
  • What number is that? (134)

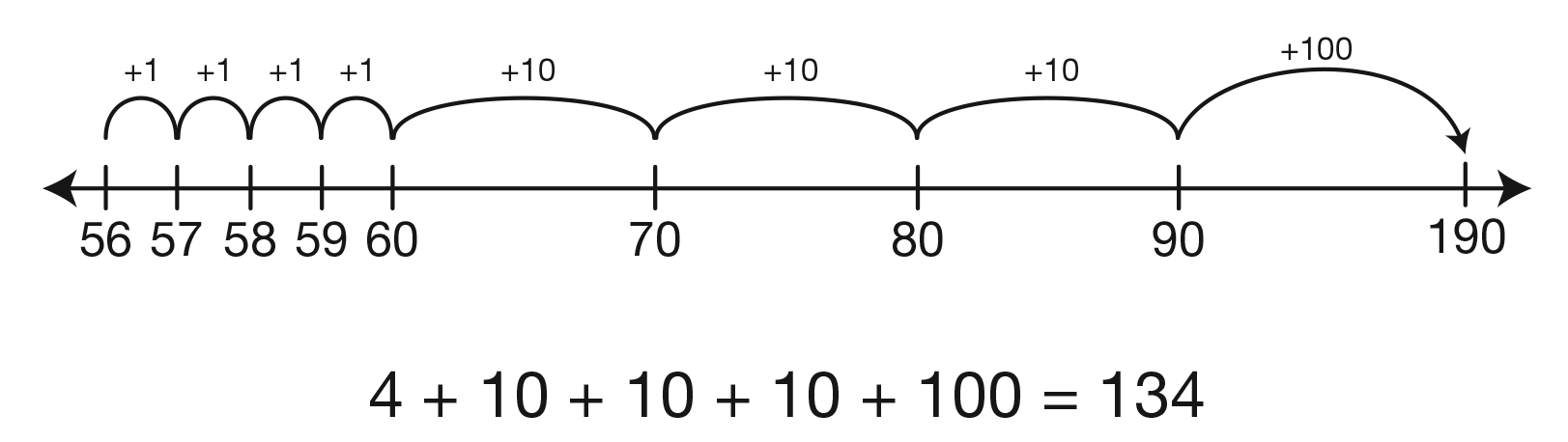
Encourage students to solve the problem a second way to check their answer. For example, they can count up from 56. See Figure 4.

The problems in the Make Trades section of the Subtract with Base-Ten Pieces pages provide practice with solving problems that involve one trade. The amount of guidance and practice needed will depend on students’ experience and comfort level with making a trade to represent a different partition of a number. Do not expect mastery immediately.

X

Use Check-In: Question 6 on the Subtract with Base-Ten Pieces pages in the Student Activity Book to assess students’ abilities to estimate differences [E5]; represent multidigit subtraction problems using base-ten pieces [E2]; subtract multidigit numbers using mental math strategies [E3]; determine the reasonableness of a solution to a subtraction problem [MPE3]; and solve a problem another way to check calculations [MPE4].

Adventure Book:
Student Activity Book: 454
Answers
X
SAB_Mini
+
Master:
57 − 39 shown with base-ten pieces
X
+
Subtraction problems with one regrouping
X
+
Solving 190 − 56 by counting on the number line
X
+