Examine a Variety of Strategies.
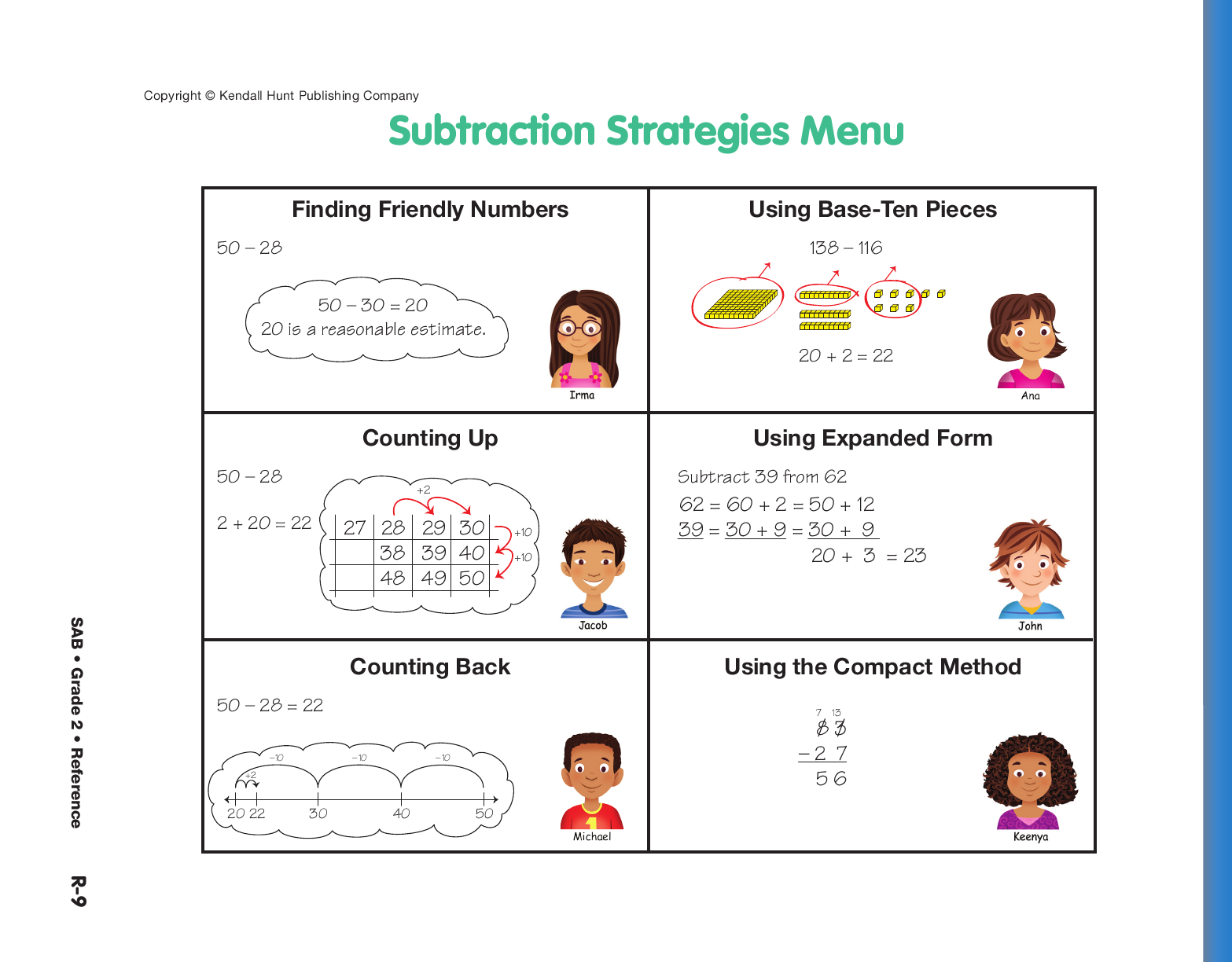
Display and direct students’ attention to the Subtraction Strategies Menu from the Student Activity Book Reference section.
- Do you recognize all the strategies given?
- Which is your favorite strategy to use? Why?
- Do you know how to use all the strategies?
- Could you use one strategy to solve every
problem? (probably)
- Do some strategies work better for some kinds of problems? (yes)
Present the problem 176 – 89 and ask students to
first estimate the sum. Review that estimation is a
way of finding reasonable, close answers and a way
of predicting or checking answers to computation
problems. Students may round using benchmarks,
use friendly numbers, compose and decompose
numbers, or count on to estimate the difference.
Then ask students to solve the problem. Encourage
them to use strategies found on their Subtraction Strategies Menu or invented strategies and tools such as number lines, base-ten pieces, or the 200 Chart.
When they have found a solution, ask:
- Compare your estimate to your answer. Does your answer seem reasonable?
- Did anyone use paper and pencil to solve this problem?
- Did anyone use mental math?
It is important that students understand there are
many valid ways to solve a subtraction problem. The
compact method is practiced in this Workshop, but
mastery should not be expected for all students at
this level, nor should it be consider the end point for
all problems. While it is certainly a useful and
important strategy, sometimes a paper-and-pencil
method is not the quickest or most efficient way to
solve a problem. Further, even though students may
conceptually understand subtraction, mistakes may
be made in notation that can lead to incorrect
answers.

The Subtraction Strategies Menu helps students choose
different, appropriate, and efficient strategies. It also allows
you to help students focus on certain strategies and not
others, as needed. For example, for students struggling
with making trades to subtract, the focus should be on
using base-ten pieces and expanded form. Ask students
who are confident with paper-and-pencil methods to use a
mental strategy to solve each problem or to try a strategy
they have not used before.
The Subtraction Strategies Menu is a summary of the
strategies and representations introduced thus far. Your
students may have a popular student-invented strategy or
representation that is not on the menu. Encourage students
to add these strategies or representations to the menu. For
example, a student may use coins to add up. To solve 30–17,
three pennies takes you to 20 cents and one dime takes you
to 30 cents, and 10 cents + 3 cents = 13 cents.
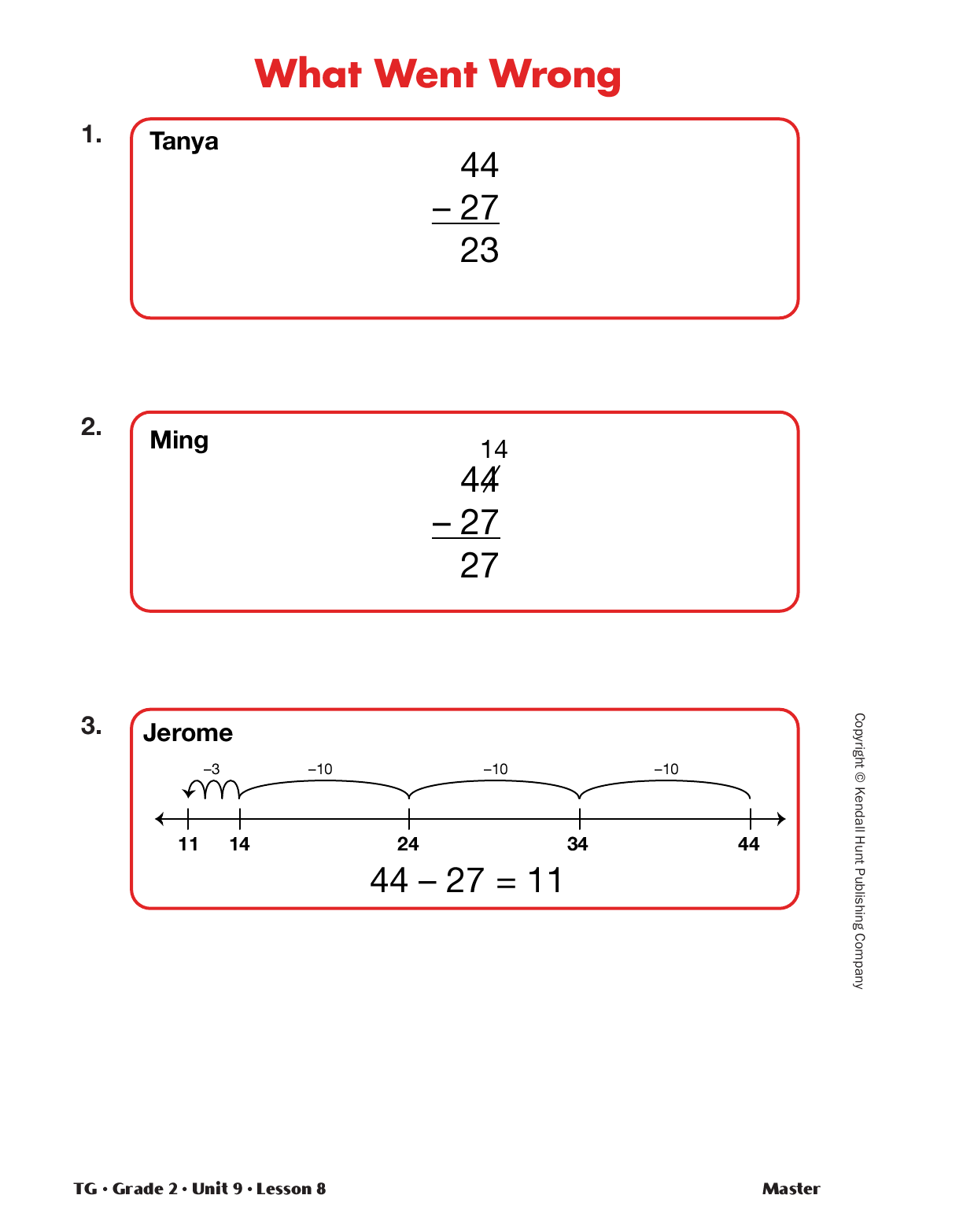
Fix Common Mistakes. Display the What Went Wrong Master. Ask students to estimate and solve
44 – 27. Show Tanya’s solution on the What Went Wrong Master.
- What do you think about Tanya’s solution? Is it correct? How do you know? (It’s wrong, because I
got 17.)
- What happens when you check by adding? (You don’t get the number you started with.)
- What would you tell Tanya to help her? (In the ones column, Tanya subtracted the smaller number
from the larger number, even though the smaller number is on top. Tanya has to trade one ten [skinny] for 10 ones [bits] before she can subtract.)
Ask a few students to share what they think and what they would say to Tanya about this incorrect solution.
Repeat a similar discussion for Ming and Jerome’s solutions on the What Went Wrong Master.
- What happens when you check Ming’s work by adding? (You get 54, not 44.)
- What would you tell Ming to help him? (Possible
response: Ming did not do his trades properly.
Four skinnies and 14 bits is not the same as 4
skinnies and
4 bits; that is, 40 + 4 is not equal to
40 + 14. He forgot to show that he traded one
skinny and only had 3 left when he put 10 more
bits in the column.)
- What happens when you check Jerome’s work by
adding? (You get 38, not 44.)
- What would you tell Jerome to help him? (Possible
response: Jerome started to count back 27. Since
27 is close to 30, he counted back 3 tens to 14.
He knew he needed to make up for the 3 that he
added to 27 to make 30, so he made 3 more
1-hops back to 11. But he should have changed
direction and added 3 hops to get 17.)
See Figure 1.
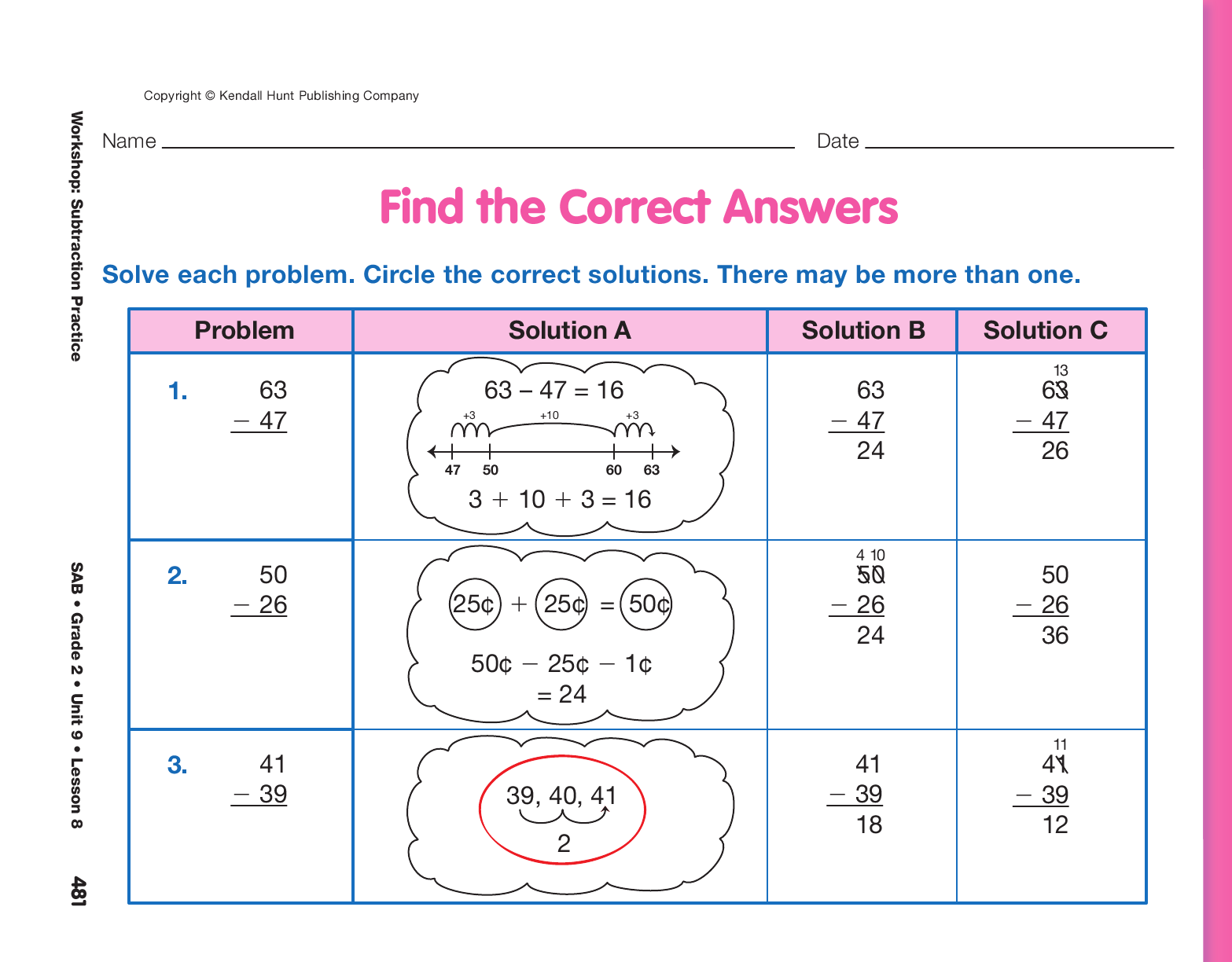
Introduce Menu and Find Correct Answers.
Display the Subtraction Practice Workshop Menu
from the Student Activity Book. See Figure 2.
Explain to students that they will use this menu to
help them choose subtraction practice. Everyone will
complete the activity listed in the first column.
Have students work in pairs to complete the Find the Correct Answers pages in the Student Activity Book. Students are asked to circle the correct solutions.
Discuss Efficiency of Strategies. Initiate a discussion
with students about efficient strategies. At this
point, students do not have enough experience to
choose the most efficient strategy for a given problem.
However, it is important for them to begin comparing
strategies. As they build experience and
confidence with the strategies, students will be better
able to select more appropriate and efficient strategies.
For now, getting students to explore the question
of which strategy makes the most sense for a
given problem is appropriate. Figure 3 lists a possible
student definition of efficiency.
Ask students to look at Questions 1–6 on the Find the Correct Answers page without looking at any of the solutions given.
- Looking at Question 2, what do you think would be an efficient way to solve this problem? (Possible response: I count count up.)
- Does it help to think about money? (26 is close to 25; 25¢ is one quarter and 50¢ is the same as 2 quarters.)
- Look at the other problems on the page. Which questions do you think would be easier to do in your head? Why?
(Possible response: I can do 78 − 38 and 41 − 39 in my head.)
- Which strategy do you think is more efficient? Why? (Possible response: It’s faster to count up with 41 − 39 than to use paper and pencil.)
- Which strategy would you prefer? Why?
- Is one strategy right and another wrong? (no)
- Are there some strategies that you will never make a mistake using? (No, you can make a mistake using any strategy.)
- How can you choose which strategy to use?
Student answers to the last question will vary.
Different students will find different strategies easier
and more understandable or efficient than others.
Observe students as they work and help them choose
strategies that are appropriate for them and that are
efficient.
Asking questions such as the following will help
them begin to decide which strategies are more efficient
than others.
- Did each way help you reach the correct answer?
- Which way did you like best? Why?
- Was there a way that was more difficult or confusing?
- Is one way done with a lot of steps?
- Can one of the ways be done in fewer steps?
- Does one way help you solve the problem more quickly?
- Which way is the most efficient or easiest to think about in your head? Why?
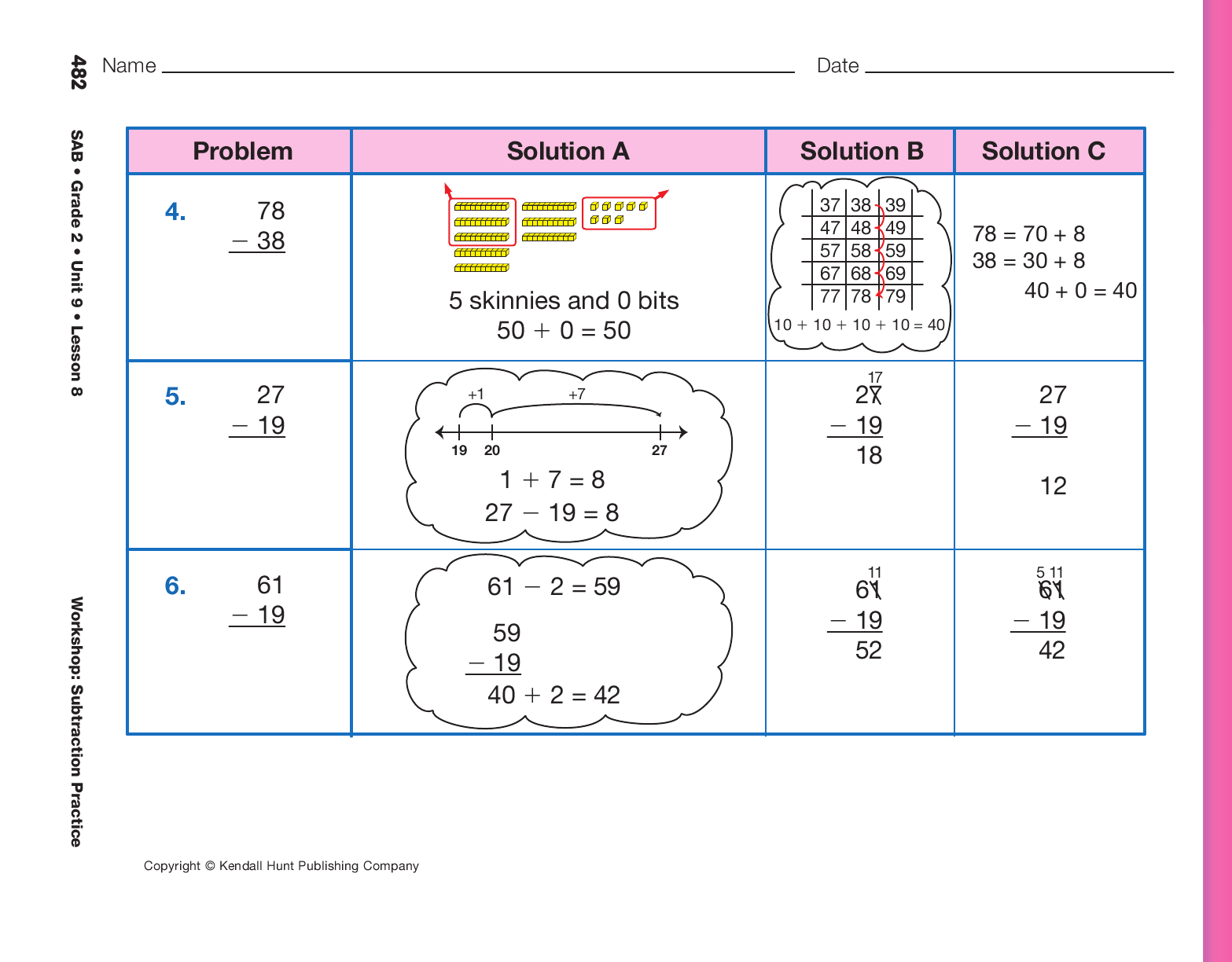
After students have had a chance to work on the
problems, discuss which solution is correct for each
problem. Then review each of the other solutions
and discuss what went wrong. For Question 6, ask
students if they can figure out what the student did
in the first strategy given and why. In that strategy,
the student changed the minuend from 61 to 59 so
that no trading would be necessary. Then the student
added the 2 back after subtracting.

- If you have students who continue to use only base-ten
pieces to solve subtraction problems, encourage them to
use expanded form as another way to show the trades or
regrouping.
- If you have students who continue to make errors when
using the compact method, encourage them to use
expanded form as another way to show the trades or
regrouping.
- If students are counting back by ones on the number line
rather than partitioning, challenge them to solve the
problem with fewer hops.
- If students are proficient with solving subtraction
problems, encourage them to find the most efficient
method or to use mental math strategies to solve the
problem.