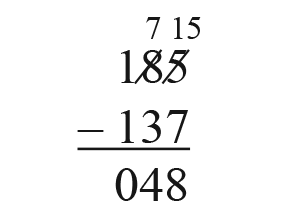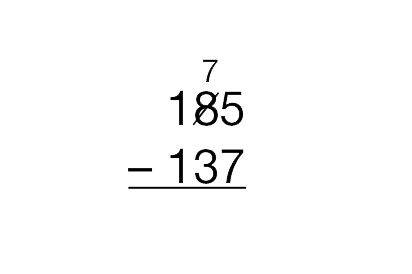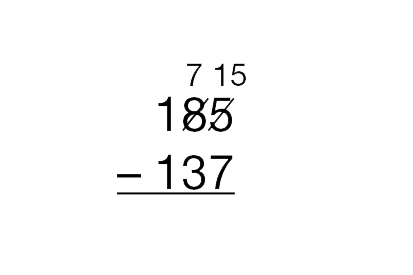Use Mental Math and Invented Strategies. Display
the problem 185 − 137 and ask students to explain
how to estimate the difference.
Display the Subtraction Strategies Chart from Lesson
2. Explain to students that they are going to solve the
same problem in many different ways so that comparisons
can be made. Tell them to choose one of the
strategies on the chart and to use it to solve 185 − 137.
For example, they may use the 200 Chart, open number
lines, base-ten shorthand, money, counting back,
counting up, or tally marks. See Figure 1.
As students work, circulate about the classroom looking
for the use of a variety of strategies. After they
solve the problem, ask several students to display their
solution strategies.
Ask questions that make connections
between the strategies such as:
- Show or tell us how you solved this problem.
- Is that answer close to your estimate? Is your answer reasonable?
- Did anyone else use this strategy? Did you get the
same answer?
- Did someone use a different strategy? Explain.
- How did [student name] show 1 hundred, 8 tens, and
5 ones?
- How did [student name] show 1 hundred, 3 tens, and
7 ones?
- Which strategy used mental math?
Use Base-Ten Pieces and Expanded Form.
Distribute base-ten pieces to students. Refer to the
same problem,
185 − 137. Have a student volunteer
use a display set of base-ten pieces to simply model
the first number in the subtraction problem as students
do the same at their desks. While students work with
base-ten pieces, record the subtraction on the board or
other display with expanded form notation. Tell students
that you are all going to work through the problem
slowly and methodically so that connections can
be made.
Through the process, ask questions that make connections between the base-ten pieces and the expanded-form notation:
- How did you model 185? (Possible response: 1 flat,
8 skinnies, and 5 bits)
- What is the value of the 1 in 185? (Possible
responses: 100, 10 skinnies, 10 tens)
- What is the value of the 8 in 185? (Possible
responses: 80, 8 skinnies, 8 tens)
- What is the value of the 5 in 185? (Possible
responses: 5, 5 bits, 5 ones)
Begin to solve the problem using the expanded-form method.
Ask the following questions and record students’ responses:
- How can you write 185 to show you have broken it
into hundreds, tens, and ones? (100 + 80 + 5)
- And 137? (100 + 30 + 7)
Display the problem:
185 = 100 + 80 + 5
137 = 100 + 30 + 7
- Why did I write the 100 over the 100, the 80 over the
30, and the 5 over the 7? (You need to line the numbers
up so that you can subtract hundreds from
hundreds, tens from tens, and ones from ones.)
Tell students to focus on their base-ten pieces. Ask the
following questions as students make trades to begin
the subtraction:
- When you subtract 137, how many ones do you need to take away? (7 ones)
- Is it possible to take 7 bits away from 5 bits? (No, there aren’t enough.)
- What should you do? (Possible response: Trade
1 skinny for 10 bits.)
- Add the 10 bits to the 5 that were there. How many
bits do you have now? (15 bits)
- How many skinnies do you have now? (7 skinnies)
- When you subtract 137, how many skinnies do you
need to take away? (3 skinnies)
- Can you take 3 skinnies away from 7 skinnies or do
you need to make another trade? (We do not need
to trade again.)
- Now subtract 3 skinnies from 7 skinnies. How many
tens or skinnies do you have left? (4 tens or
4 skinnies)
- Did you need to trade any flats for skinnies? (no)
- Can you take 1 flat from 1 flat? How many do you
have left? (Yes, we have 0 flats left.)
- What value do the remaining base-ten pieces have? (4 skinnies and 8 bits or 48)
- Does that answer match the solutions you found in
the beginning of the lesson? (yes)
- When you use base-ten pieces, does the order in which you subtract make a difference? Could you
subtract the skinnies from the skinnies first and then the bits from the bits? (The order doesn’t make a difference.)
Direct students’ attention back to the expanded form
notation. Record their trades by extending the problem:
185 = 100 + 80 + 5 = 100 + 70 + 15
137 = 100 + 30 + 7 = 100 + 30 + 7
- How did I show that we took 1 skinny from the
8 skinnies? (You wrote 70 to show that we have
7 skinnies left.)
- How did I show you have 15 bits? Where did the 15
come from? (We traded the 1 skinny for 10 bits and
added them to the 5 bits. You wrote 15 to show the
15 bits.)
Point to displayed notation.
- Does 100 + 80 + 5 = 100 + 70 + 15? (yes)
- How can you show that with your base-ten pieces?
Is 1 flat, 8 skinnies, and 5 bits the same as 1 flat,
7 skinnies, and 15 bits? (Yes. We traded one skinny
for 10 bits but all the pieces still add to 185.)
Count out the base-ten pieces with students. Direct students’
attention to the displayed notation as you point
to the numbers.
- When I rewrote the problem, the 80 changed to 70
and the 5 changed to 15. Why did the 100 stay the
same? (You did not need to trade the 100 for 10
tens. We did not need to trade the flat for 10 skinnies
so the 100 stayed the same.)
- When you use expanded form, can you start by subtracting
the ones, then the tens, and then the hundreds? (yes)
- Can you also subtract the hundreds first, then the
tens, and then the ones instead? (yes)
- Do you get the same answer each way? (yes)
Complete the subtraction working from the left to the
right, and then from right to left to show that subtraction
can start either way with the expanded-form
method:
185 = 100 + 80 + 5 = 100 + 70 + 15
137 = 100 + 30 + 7 = 100 + 30 + 7
0 + 40 + 8 = 48
- Does this answer match the answer you found with
base-ten pieces? (yes)
- Which of these methods or strategies do you like the best?
Use Compact Method. Display the same problem as written below:
185
− 137
Explain to students that you will all solve the problem
one more time, this time using the compact method.
Instead of using base-ten pieces, ask them to imagine
the pieces.
- There are no labels for the columns and lines to separate
the hundreds, tens, and ones. Which column is
the hundreds column? Tens column? Ones column?
(Possible response: The ones column is on the
right, the tens column is next to the ones column in
the middle of the number, and the hundreds column
is on the far left.)
- Let’s start at the ones column. Can you subtract
right away or do you need to make any trades? How
do you know? (You have to trade because if you
think about base-ten pieces, you can’t take 7 bits
from
5 bits.)
- Can you just take 5 from 7 instead? Why or why not?
(Possible response: If you think about base-ten
pieces, when you start the problem you place 5 bits
for 185. It is the starting number. You take the
pieces away from the starting number. You don’t
take pieces away from the other number.)
- Imagine the trade in your heads. What will you do? (Trade 1 skinny for 10 bits.)
- Do you still have 8 tens? (No; we took away one
ten, like a skinny, when we traded. So now we only
have
7 tens or 7 skinnies.)
- How do you show that? (Possible response:
Cross out the 8 in the tens column and write a
7 for 7 tens.)
- Let’s write that down. I’ll cross out the 8 and write 7
in the tens column. [See Figure 2.]
- If you trade one of the skinnies for 10 bits, how many
bits do you have? (You have 10 plus 5 bits. That’s
15 bits.)
- Let’s write that down. I’ll cross out the 5 and write 15
in the ones column. Why did I write the 15? (It
shows the 15 bits. It’s 5 + 10 more.) [See Figure 3.]
- Is 7 tens and 15 ones the same as 8 tens and
5 ones? (Yes; you changed the number of bits and
skinnies but they add up to the same number. 8 tens
and 5 ones is the same as 7 tens and 13 ones. They
are both 85.)
- How is this step like writing 80 + 5 = 70 + 15 in the
expanded-form method? (It is the same thing. We
are trading and just rewriting the numbers to show
how we are regrouping them.)
- Can you subtract the tens or do you need to trade a
flat for skinnies? How do you know? (We can take
3 tens from 7 tens so we don’t have to trade a flat for skinnies.)
- Now finish the problem by subtracting 15 − 7 in the
ones column, 7 − 3 in the tens column, and 1 − 1 in
the hundreds column. What is the answer? (48)
Demonstrate how to record the subtraction on the display:
- Did we get a reasonable answer? (Yes, because we got 48 every time we solved the problem.)
- Show how to check the subtraction with addition. (If 48 + 137 = 185, then we have the correct answer.)
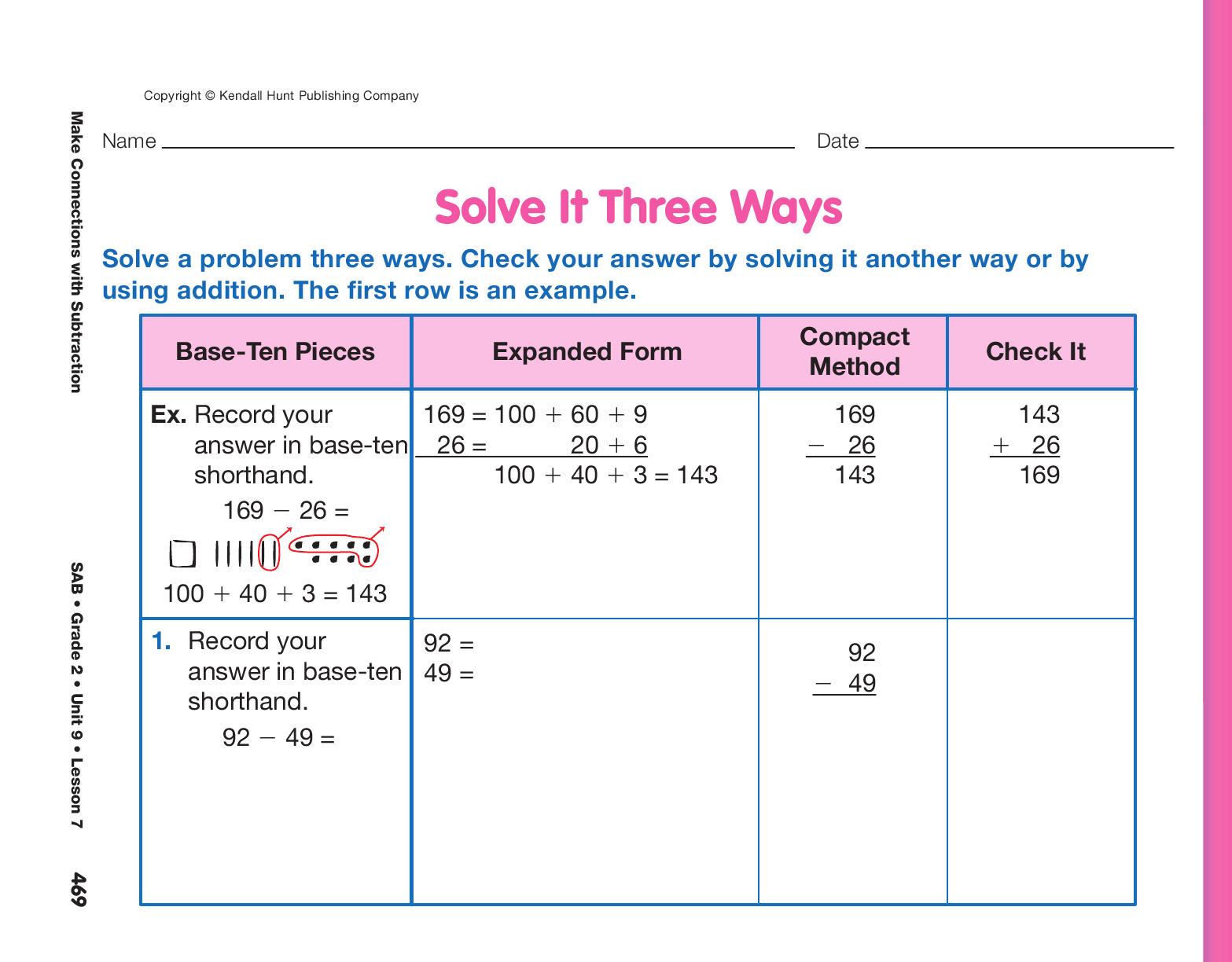
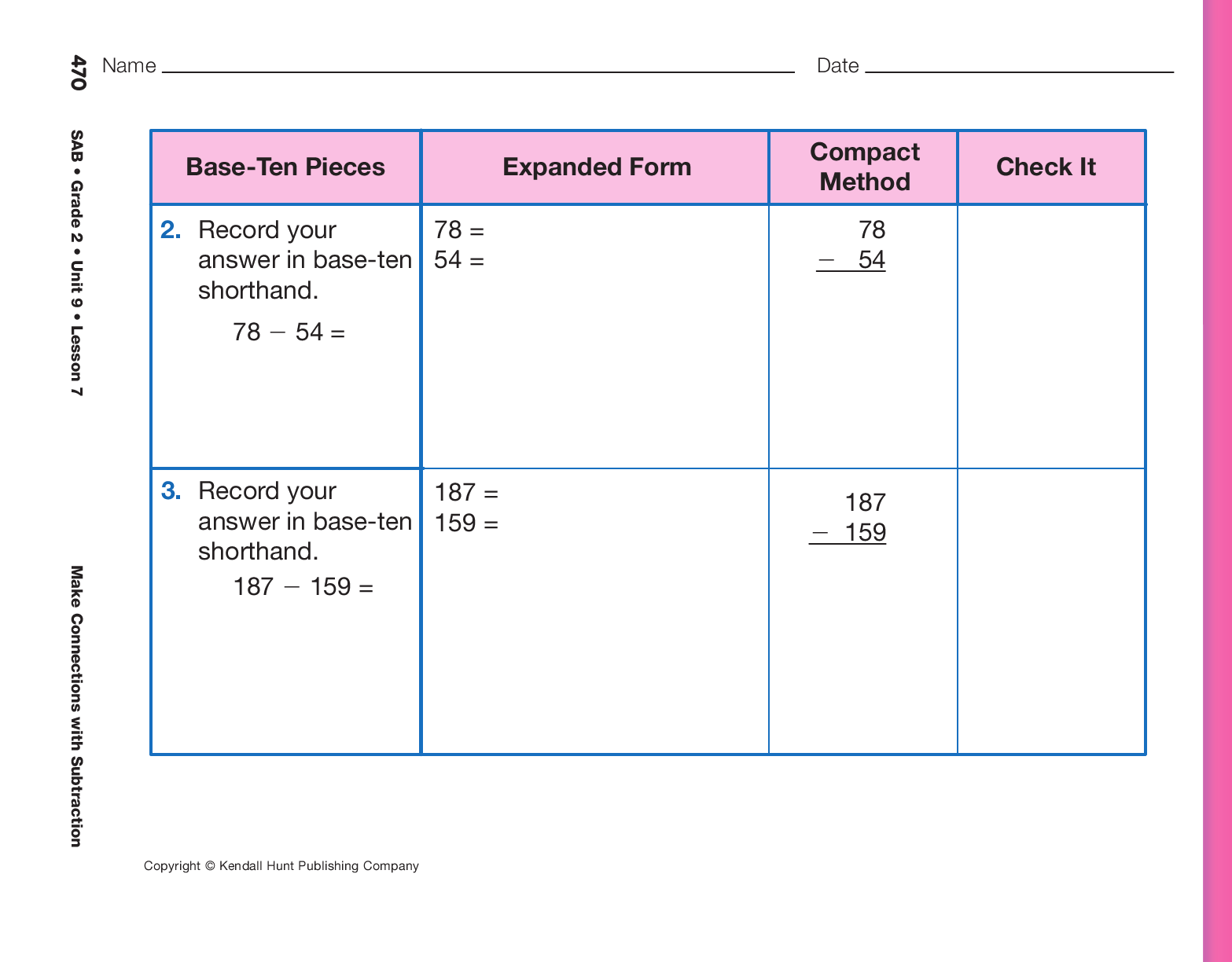
Assign the Solve It Three Ways pages in the Student Activity Book. Students will solve the same subtraction
problems three different ways: using base-ten pieces
and recording the difference in base-ten shorthand, and
with the expanded–form and compact methods.
Encourage students to check their answer by using
strategies such as the following:
- Solve the problem a different way using a strategy on the Subtraction Strategies Chart from Lesson 2.
- Use a number line.
- Use a 200 Chart.
- Think of money.
- Check by using addition.
Assign Home Practice Parts 4–5 for homework after Part 1 of the lesson.