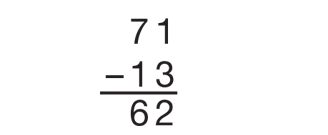Lesson 6

Paper-and-Pencil Subtraction: Compact Method

Est. Class Sessions: 2–3

Developing the Lesson

Part 2: Checking for Reasonableness

X

Most of the errors students make when using the compact method in subtraction are notation errors rather than conceptual errors. For example, in a three-digit subtraction problem that requires trading a ten for ones, students will often cross out a hundred and trade it for 10 ones. Math Trailblazers focuses on helping students build number sense by developing opportunities to understand place value, invent strategies, recognize subtraction as an inverse operation of addition, and use a variety of tools to solve problems before moving on to more traditional algorithms. Although the compact method is introduced in this lesson, some students will still need to use other tools and strategies to solve subtraction problems; therefore, mastery should not be expected for all students at this level.

Use Strategies to Check Solutions. It is very important for students to develop the habit of checking their work. However, when they look back over calculations, students often make the same mistakes they made the first time. For this reason, it is helpful to check by doing the problem another way. See the Sample Dialog for common mistakes students might make when using the compact method.

Encourage students to check their answer by using strategies such as the following:

  • use the expanded form
  • use base-ten pieces
  • use friendly numbers by rounding to nearest tens
  • use a number line to make jumps of tens and ones
  • use a 200 Chart
  • think of money
  • mentally subtract first the tens and then the ones from the beginning number (e.g., 71 − 10 = 61 and 61 − 3 = 58)
  • check by using addition
X

Use this Sample Dialog to discuss

subtraction problems using the compact

method.

Teacher: How did you solve 34 − 26?

Eric: I started in the ones column. I said
4 − 6 = 2. In the tens column I said
3 − 2 = 1. My answer is 12.

Teacher: Is the answer reasonable?

Lauren: I don’t think so because to go from 26 to 30 is 4 and to go from 30 to 34 is 4 more. I think the answer is 8.

Teacher: What do you think happened when you solved the problem, Eric?

Eric: Oh, when I looked in the ones column, I couldn’t subtract 4 − 6, so I subtracted up and said 6 − 4 = 2.

Teacher: Remember that we’re starting with the top number and taking away the bottom number. What can you do if you don’t have enough ones?

Nancy: I would trade one of the tens for
10 ones and add it to the 4 ones. Then I would have 14 ones. I would subtract
14 ones − 6 ones and 2 tens − 2 tens. My answer is 8.

Ana: My answer is 4. What did I do wrong?

Teacher: Explain how you solved the problem.

Ana: First, I said I can’t subtract 4 − 6, so I traded a skinny for 10 bits. Then I subtracted 10 − 6 = 4 and 2 − 2 is 0. My answer is 4.

Javier: I think I know what you did wrong. When you traded 1 skinny for 10 bits, you forgot to add it to the 4 bits that
were in the ones column before. You should have 14 bits 14 − 6 = 8 and
2 − 2 is 0. The answer is 8.

Teacher: How did you solve 67 − 22?

Chris: I got 315 for an answer. I said I can’t subtract 7 − 2, so I crossed out the 6 and that leaves 5 tens. Then I added
10 to the 7 ones and I wrote 17.
17 − 2 = 15 and 5 − 2 = 3. My answer
is 315.

Teacher: Is that a reasonable answer?

Frank: No, if you start with 67 and you subtract 22, how could you have 315 for an answer?

Teacher: What do you think happened?

Chris: I don’t know when I have to make trades.

Frank: I think he crossed out the tens without thinking if he could subtract 7 − 2. In the ones column you can subtract 7 − 2 without making any trades and in the tens column 6 − 2 = 4, so the answer is 45.

Teacher: It’s important to think about whether or not you have to make trades. If you have enough ones to subtract the bottom number, you don’t have to trade a ten for ones. How did you solve 253 − 126?

Maria: I got 37, but when I used the number line I got a different answer. What did I do wrong?

Teacher: Demonstrate how you solved the problem.

Maria: I couldn’t subtract 3 − 6, so I went to the hundreds column and crossed out the 2 and traded one hundred for 10 ones. Then I added it to the 3 ones and I got 13. Thirteen minus 6 is 7, 5 tens − 2 tens is 3, and 1 hundred
minus 1 hundred is 0. My answer is 37.

Ashley: I know what happened! You traded
1 hundred for 10 ones and you should have traded 1 ten for 10 ones. You have to go to the tens column to trade—not the hundreds.

Maria: Oh, I understand now! The answer is 127. That matches what I got on the number line!

Teacher: Good thinking! After you solve the problem, check to see if the answer is reasonable. If not, go back and try it again.

Begin by writing a subtraction problem with an incorrect answer on a display as shown in Figure 6.

Ask:

X
  • Is the problem correct? (no)
  • How do you know? (Possible response: When I did the problem I got 58.)
  • How can you check to see if the answer is reasonable? (Possible response: Use friendly numbers.)

Checking with Addition. Students might suggest several different ways to redo the subtraction problem. But they might need prompting to come up with a way to check subtraction by using addition.

Explain:

X
  • You can check your answer to see if it’s correct by using addition.
  • Add the answer to the number you subtracted and you should get the number you started with. In this case, I will add 62 to 13 and I should get 71.

Demonstrate by writing the answer 62 and adding 13.

Ask:

X
  • If you add 62 + 13, the answer is 75. Is that the number I had at the beginning? (no)
  • Then, I know my answer is not correct.

Give students a few subtraction problems as in Figures 7 and 8. Ask students to check the answers. After checking with addition, students should see that the subtraction is correct in Figure 7. Adding 26 back to the answer (19) gives what you started with (45). After checking with addition, students should see that there is a mistake in Figure 8. Adding 37 back to the answer (33) does not give you what you started with (64). Discuss the possibility that either the subtraction is incorrect or the addition is incorrect, but there is a mistake somewhere.

Ask students to solve the problems on the Check with Addition page in the Student Activity Book. In Question 1A and Question 1B students use addition to check someone else’s work. In Question 2A and Question 2B, they subtract and then use addition to check their own work.

Adventure Book:
Student Activity Book: 465
Answers
X
SG_Mini
+
Master:
A problem with an incorrect answer
X
+
Checking a correct subtraction problem with addition
X
+
Checking an incorrect subtraction problem with addition
X
+