Is It Reasonable

Est. Class Sessions: 1–2

Developing the Lesson

Estimate to Check Reasonableness. Read the following scenario aloud:

I stopped at a pretzel stand. The pretzel I wanted cost 29¢. I gave the seller one dollar. He handed me back 2 quarters and 1 nickel. I told him that he had returned the wrong amount because I knew my change should have been about 70¢.

Ask:

How did I know about how much change I was supposed to get without figuring out the exact answer? (You estimated.)
How many cents are 2 quarters and a nickel? (55 cents)
What words and numbers do you need to solve this problem? (100 cents − 29 cents = cents)

Record the number sentence on the board.

Does 55 cents in change make sense? (no)
What are some ways to estimate about how much change I should have received?

Encourage students to describe their estimation strategies. List the strategies suggested on the board or chart paper. Some possible strategies are shown in Figure 1.

Display the Subtraction Strategies Chart from Lesson 2. Have students refer to it as they solve subtraction problems. See Content Note.

Ask:

Solve 100 − 29 to find an exact answer to the problem. Use labels in your answer so we know what the numbers mean.
(100 cents − 29 cents = 71 cents)
How does your answer compare to your estimate? Does your answer make sense?

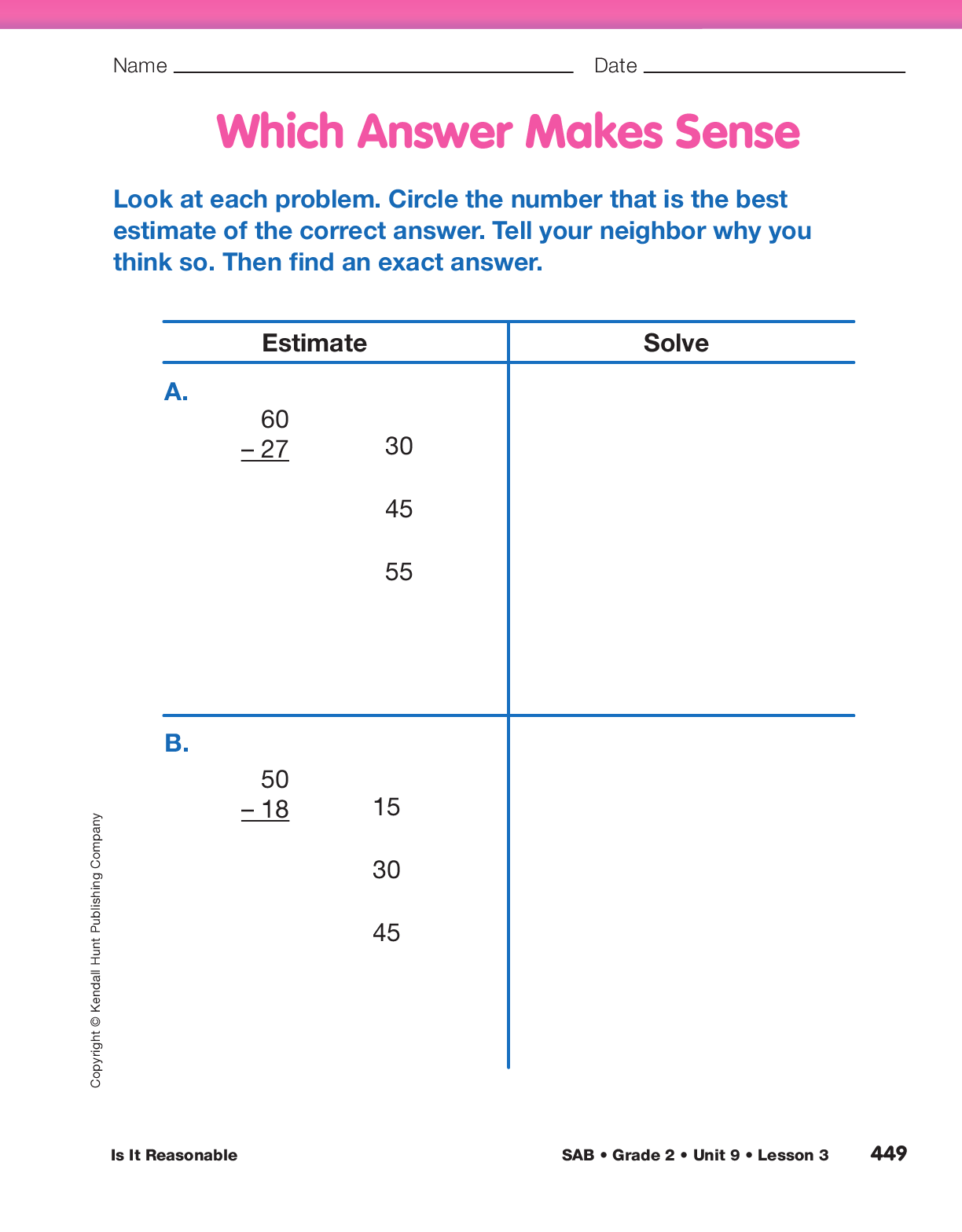
Choose an Estimate. Write the numbers 40, 55, and 65 on the board next to the following subtraction problem:

72
− 15

Ask:

What is the answer to a subtraction problem called? (difference)
What does reasonable mean? What other words do you think of when you hear the word “reasonable”? (Possible response: Reasonable means it makes sense.)
Estimate which of these three numbers is a reasonable solution for this problem. Is 40 a reasonable difference? Why or why not? (Possible response: 40 is not reasonable. In order to get 40 I would have to subtract 30 from 70. 15 is not close to 30, so 40 is not a reasonable answer.)
Is 65 a reasonable difference? Why or why not? (Possible response: 65 is not a reasonable answer because 65 is closer to 72 than 15 spaces on my 200 Chart. Five spaces will get me to 70, and I only need to go 2 more spaces to 72.)
Is 55 reasonable? How do you know? (Possible response: 55 is reasonable. I used my number line. If I subtract 10 from 70 I get to 60. And another 5 more will get me to 55.)
When you estimate the answer to a subtraction problem before solving it, the estimate gives you an idea of about how much your exact answer should be. Explain in your own words how knowing that 55 is a reasonable estimate can help you with this problem. (Possible response: I know that when I take 15 from 72 that my answer should be around 55. If it is much greater or smaller than 55, I need to recheck my work.)

Display and direct students’ attention to the Math Practices page in the Student Activity Book Reference section. Remind them that Math Practice Expectation 3, Check for reasonableness, focuses on looking back at an answer to see if it makes sense.

Now that students have determined that 55 is a reasonable difference, ask them to use any subtraction strategy to find an exact answer to the problem. The reasonable estimate will help students identify when a mistake may have been made.

Have students look at their answers, or have a volunteer demonstrate how he or she solved the problem, and ask:

Compare your answer to your estimate. How do you feel about your answer? (Possible response: I feel confident about my answer because it is close to the estimate of 55.)

Direct students’ attention back to the Math Practices display.

Focus on Math Practice Expectation 4, Check my calculations.

Estimating helps you know if you need to check your calculations. If you think that your answer is not reasonable, you may have made mistakes. How could you check your calculations? (Go back and look for mistakes; try solving the problem another way.)

Continue estimating answers for subtraction problems. Give students answer choices for which they have to determine whether the answers are reasonable. Some possible examples are:

84 − 29 (30, 50, 70) 63 − 18 (40, 50, 60)

Ask students to estimate which of the three numbers is a reasonable solution for each problem. Discuss each number and ask students to explain why it is or is not reasonable.

Assign the Which Answer Makes Sense pages in the Student Activity Book to student pairs. Students find the best estimate for each problem. Encourage them to explain to a partner how they determined the best estimate for each problem. Then students will find an exact answer to the problem using any subtraction strategy they choose.

Estimate and Solve. Present this word problem to the class:

You buy a jumbo pretzel that costs 59 cents. You pay with three quarters. How much money should you get back from the seller?

Have students discuss the problem with a partner, then ask:

What does the problem ask you to find out? (how much change I should receive)
What words and numbers do you need to solve the problem? Can you write a number sentence?
(75 cents − 59 cents = cents)

Instead of giving students answer choices, ask them to estimate the difference with their partner. As students work, circulate and look for examples of a variety of estimation strategies.

Select several student volunteers to share how they estimated, recording their work on chart paper. Try to have examples of different strategies such as using coins, intervals, number lines, the 200 Chart, and using friendly numbers. See Figure 1 for several estimation strategies.

Finally, ask students to find an exact answer to the problem. As described in MPE6, Use labels, remind students to include a label in their answer so that it is clear what the numbers mean.

Ask a student volunteer to show his or her subtraction solution and ask:

What was your estimate to the problem 75 − 59?
Show how you solved the problem.
What label did you include in your answer? (cents)
Compare your estimate to your exact answer. How do you know that your answer is reasonable? (If my answer is close to my estimate, then I know it makes sense and is reasonable.)
What would you do if your answer did not make sense? (I would look back for mistakes and I would try to solve the problem using a different strategy.)

Remind students of Math Practice 4, Check my calculations. If after comparing their estimate to their answer any students feels like they made a mistake, encourage them to solve the problem again using a different strategy.

Assign the Pretzel Problem page in the Student Activity Book for students to complete individually. Encourage them to use a 200 Chart, number lines, base-ten pieces, friendly numbers, or any other tool or strategy you have used in class to help them estimate and solve the problem. They may refer to the list of estimation strategies the class made on chart paper, the Subtraction Strategies Chart from Lesson 2, and the Math Practices page in the Student Activity Book Reference section.

Use the Pretzel Problem page with the Feedback Box in the Student Activity Book to assess students’ abilities to estimate differences using mental math strategies [E5, MPE2]; subtract multidigit numbers using mental math strategies [E3]; know the problem [MPE1]; check for reasonableness [MPE3]; check calculations [MPE4]; and show work [MPE5].

Adventure Book: