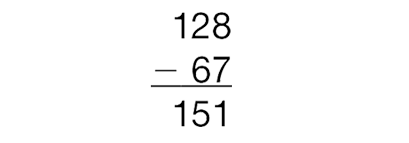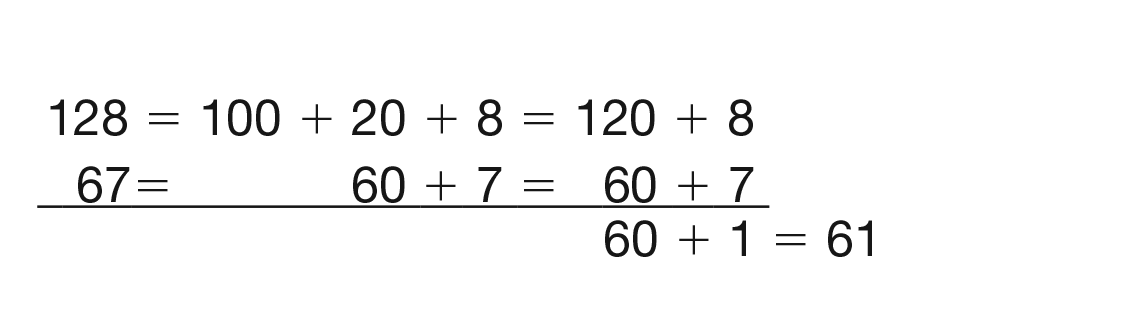Use Addition to Check Calculations.
Students
were introduced to the concept of using addition to
check their subtraction in Lesson 4. Explain to students
that it is very important for them to develop
the habit of checking their work. Tell them that the
nice thing about subtraction is that you can check it
with addition. Sometimes when you look back over
calculations, you make the same mistake you did the
first time. But by checking subtraction with a different
operation—addition—you can sometimes pick
up errors you would not otherwise catch.
Begin by displaying a subtraction problem with an
incorrect answer, as in Figure 6.
- Is the answer to this problem correct? (no)
- How do you know? (Possible responses: The
answer doesn’t make sense because it is more
than what you started with; I estimated and the
answer should be about 60; I subtracted and got 61.)
- Is there a way to check without subtracting? (We could use addition to check the subtraction.)
Remind students that in a subtraction problem, you
start with a number and subtract something. If you
add back what you subtracted, you should get the
number that you started with. If you do not, you
must have made a mistake.
- If I added 67 back to my answer, what should I get? (the number you started with, 128)
- Add 67 to 151. Do you get 128? (no)
- What does that mean? (It means you must have made a mistake.)
Assure students that it is not a weakness to check
their work but a strength. Even the best mathematicians
make mistakes in their calculations. One thing
that makes them “the best” is that they have the habit
of checking their work so they can find and correct
their mistakes.
Solve and Check Subtraction Problems with
Trades. Next have the students solve the same
problem, 128 − 67, with base-ten pieces.
- How did you show 128 with base-ten pieces using
the Fewest Pieces Rule? (1 flat, 2 skinnies, and
8 bits)
- How did you take 67 away from 128? Did you have to make any trades? Show or tell us what you did. (Possible response: I could take 7 bits away from
8 bits but I couldn’t take 6 skinnies away from
2 skinnies. I traded 1 flat for 10 skinnies. Then I
had 12 skinnies and took 6 away.)
- What happens when you are subtracting and you
don’t have enough skinnies? (You take one of the
flats away and trade it for 10 skinnies. Then you
can take away as many skinnies as you need.)
- What if you don’t have enough bits? (You can do
the same thing—you trade. You can trade
1 skinny for
10 bits.)
- Does trading change your number? (No. 10 skinnies
is the same as 1 flat, and 10 bits is the same
as
1 skinny, so the value of the number stays the
same.)
- Did anyone solve 128 − 67 a different way? Show
or tell us how you solved it. (Possible response: I
traded all the pieces right away. I traded the flat
for 10 skinnies and then had 12 skinnies to work
with. Then I started subtracting.)
- What was your answer? (61)
- Now solve the same problem using expanded form and let’s see if you get the same answer.
[See Figure 7.]
Ask a student to display and demonstrate how they
solved the problem using expanded form.
- Is this the same answer you got when you solved
the problem using base-ten pieces? (yes)
- Was [student name] able to start subtracting right
away or did [he] need to make some trades? How
did [student name] subtract 60 from 20? (Possible
response: He could take 7 from 8 right away,
but a trade had to be made because you can’t
subtract
60 from 20. He traded 100 for 10 tens.
10 tens plus
2 tens is 12 tens or 120. Then he
could do 120 − 60.)
- How was this like trading with the base-ten
pieces? (Adding the 100 to the 20 is like trading
1 flat for
10 skinnies and adding it to the 2 skinnies.)
- Does 100 + 20 + 8 = 128? (yes)
- Does 120 + 8 = 128? (yes)
- It looks like you did a good job trading, but let’s
check the subtraction with addition to make sure
the answer is correct. What is the answer to the
subtraction problem? (61)
- What did you take away? (67)
- What is 61 + 67? (128)
- What number did you start with? (128)
- What does that tell you? (The calculations are
correct and 61 is the right answer.)
Display the following problem:
100
− 68
Students often have trouble with problems such as
this, particularly as they work with larger numbers.
However, in Lesson 2, students solved many similar
problems when they practiced making change from a
dollar. Remind them of this and ask them to solve
the problem using a strategy or tool they used in
Lesson 2. Then ask them to solve the problem using
base-ten pieces. Ask a student to show the solution
with display base-ten pieces. Note how the student
models 100, whether with a single flat or with
ten skinnies.
- How do you show 100 with base-ten pieces?
(Possible response: I used a flat. A flat is the
same
as 100.)
- Did anyone start out by representing 100 a different
way? (Possible response: I used ten skinnies
because I know that 10 skinnies is 100.)
- Can you say that using tens? (10 tens is 100.)
- Is it okay to start with ten skinnies when your first
number is 100? Why or why not? (Yes, because it
is the same thing. 10 skinnies is the same as 100.)
- How did that change the steps you needed to
solve the problem?
If students start with a flat, they have to trade twice,
the flat for ten skinnies, and then one skinny for
ten bits. If a student starts with 10 skinnies, only
one trade is necessary, one skinny for ten bits.
Practice Using Addition to Check Subtraction.
Introduce the Check Subtraction with Addition pages
in the Student Activity Book by reading the short
vignette. Assign the pages to student pairs. Students
will use expanded form to solve subtraction problems
and then check their answers with addition.
Allow access to base-ten pieces if students would
like to use them.