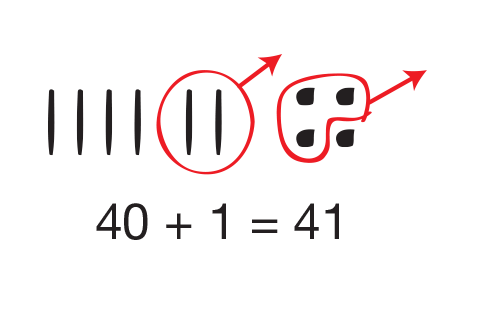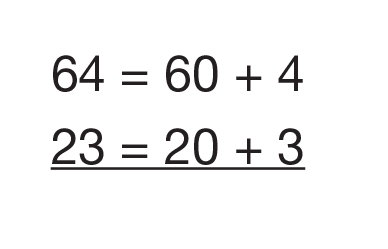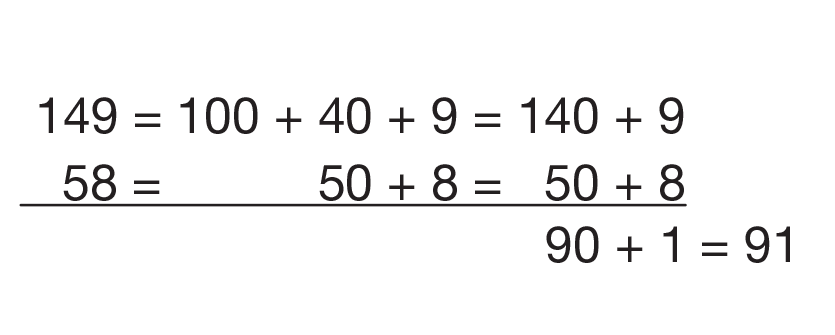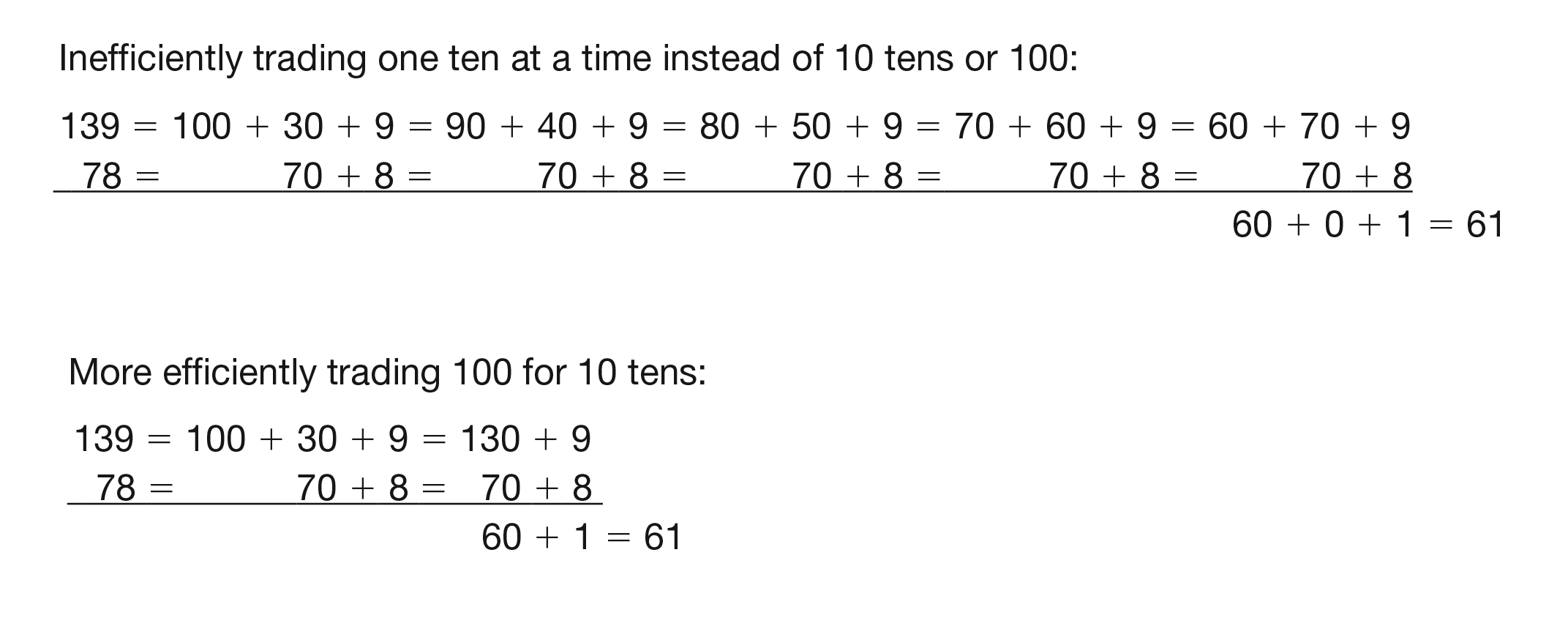Paper-and-Pencil Subtraction: Expanded Form

Est. Class Sessions: 2–3

Developing the Lesson

Part 1: Connect Base-Ten Pieces to Expanded Form

Expanded Form Addition. The expanded form shows a number expanded into an addition statement. Forty-three in expanded form is 40 + 3. Using the Fewest Pieces Rule, one hundred twenty-five in expanded form is 100 + 20 + 5. However, 100 + 10 + 15 also shows 125 in expanded form because the number is decomposed into hundreds, tens,
and ones.

Solve Subtraction Problems with No Trades. Students practiced subtraction with base-ten pieces in Lesson 4. Now you can discuss how they can use expanded form as one way to solve subtraction problems with paper-and-pencil. Remind them that they have previously used expanded form to solve addition problems. See the Content Note on expanded form addition.

Display the following problem that requires no trades, vertically:

64
− 23

Ask students to estimate the difference. Then ask students to model and solve it with base-ten pieces as shown in Figure 1. When modeling subtraction ask students to place the first number in the problem, the minuend, 64. Then they should show the subtraction by taking away pieces that represent the second number, the subtrahend, 23. As students work with the base-ten pieces, be sure they do not begin the problem by laying out the pieces for both numbers.

Direct students’ attention back to the displayed problem. Ask a student volunteer to extend the notation by writing it in expanded form as shown in Figure 2.

Remind students that this is a subtraction problem. The plus signs in the problem written this way simply refer to the different ways of partitioning the numbers. This doesn’t change it from a subtraction problem. See the Content Note on expanded form subtraction. Draw students’ attention to the way the columns are aligned in this notation so that tens are subtracted from tens and ones are subtracted from ones.

Expanded Form Subtraction. We intentionally left the subtraction sign out of the expanded form solution to the problem. Including it only on the left would make a mathematically incorrect sentence. A correct sentence would be − 64 = − (60 + 4), but students haven’t worked with parentheses yet, so this would be confusing. If students become confused by the presence of the plus signs in a subtraction problem, try writing the expanded form like this:
64 = 60 and 4
23 = 20 and 3
40 and 1 = 41

Have students relate their base-ten pieces to the problem written in expanded form.

Ask:

How does the problem written this way relate to the base-ten pieces? How is the 60 + 4 shown with your base-ten pieces? (That was what we started with:
6 skinnies, which is 60 and 4 bits, which is 4.)
How is the 20 + 3 shown in your base-ten pieces? (That was what we took away: 2 skinnies and 3 bits.)

Show the subtraction step on the problem written in expanded form. Sixty minus 20 is 40 and 4 minus 3 is 1. Subtraction in this lesson can be done in any order. Students should be allowed to choose whether they subtract the ones or the tens first.

64 = 60 + 4
23 = 20 + 3
40 + 1 = 41

Ask:

Solving a problem two ways allows you to check your answers. Does this answer agree with your answer in base-ten pieces? (yes)

Solve Subtraction Problems with Trades. Display a problem such as 57 − 29, which requires a trade. Have the class estimate the difference. Then ask students to use base-ten pieces to solve it. Remind them to place 57 pieces and then to remove 29 of them. Ask a student volunteer to model the problem with display base-ten pieces, showing the trade.

Ask:

Could you take 9 bits from 7 bits? (no)
What did you do? (I traded 1 skinny for 10 bits. Then I added all the bits together, 10 + 7, and I had 17 bits to work with.)

Write the problem in expanded form.

57 = 50 + 7
29 = 20 + 9

Ask:

What do you notice about this problem? Are you ready to start subtracting? Can you subtract 9 from 7? (No, you can’t take 9 from 7 so you need to trade a ten for ten ones.)

Extend the written problem by writing:

57 = 50 + 7 = 40 + 17
29 = 20 + 9

Ask:

Is 57 the same as 50 + 7? (yes)
Is 57 the same as 40 + 17? (yes)
Is 50 + 7 = 40 + 17? (yes [See the Content Note on making trades])
How do you know? (Both sides of the equal sign
show 57.)
Can you show that 50 + 7 equals 40 + 17 with base-ten pieces? (5 skinnies and 7 bits is the same as
4 skinnies and 17 bits.)
Where did the 17 bits come from? (When you trade
1 skinny for 10 bits, you then have 17 bits.)
Why did I write 40? 17? (You don’t have 5 tens or 50 after the trade. You have 4 tens or 40 and 17 bits. You added the 10 to the 7 to get 17.)

Complete and display the written version of the problem.

57 = 50 + 7 = 40 + 17
29 = 20 + 9 = 20 + 9

Show the subtraction step. Forty minus 20 is 20 and 17 minus 9 is 8. Complete the problem by adding 20 + 8.

57 = 50 + 7 = 40 + 17
29 = 20 + 9 = 20 + 9
20 + 8 = 28

Making Trades. Students frequently do not understand that when they make trades (or regroup) in order to subtract they are just partitioning the top number in a different way. It is important for them to realize that the new representation should have the same value.

Trade 100 for 10 Tens. Work through a problem that involves trading 100 for 10 tens. Display the following problem:

149
− 58

Tell students to estimate the difference, solve the problem using base-ten pieces, and then ask them to help you solve the problem using the expanded-form method. See Figure 3. Point out that you lined up the hundreds, tens, and ones. There are no hundreds in 58 so you left a space in the hundreds column.

Some students may have difficulty with the notation when the trade for 100 is made. They may want to add 10 to the 40 (and write 50) rather than 10 tens, 100, to the 40. This is inefficient. If students are recording the trade inefficiently, remind them that they are breaking the flat into 10 skinnies and adding these
10 skinnies to the existing 4 skinnies, or adding 100 + 40. See Figure 4 for an example of inefficient trading.

After they have solved the problem with base-ten pieces and expanded form, ask questions that connect the base-ten pieces to the paper-and-pencil solution:

When you used base-ten pieces, were you able to take 5 skinnies from 4 skinnies? Did you need to make any trades? (I couldn’t take 5 skinnies from
4 skinnies so I traded 1 flat for 10 skinnies.)
How many skinnies did you have then? (14 skinnies)
How much is 14 skinnies? (14 tens or 140)
When you used expanded form, could you subtract 50 from 40 or did you need to make a trade? (I had to trade 100 for 10 tens, just like I traded 1 flat for
10 skinnies.)
How is that trade shown in expanded form? Think about 14 skinnies. (I traded the 100 for 10 tens and added it to 40 to make 140, just like the 14 skinnies.)

As needed, present students with a few other problems to practice. Sample problems are shown in Figure 5. Work through a problem that involves subtracting a 3-digit number from a 3-digit number making sure that students align the hundreds with the hundreds, tens with tens, and ones with ones. Display some problems horizontally and some vertically to make students comfortable seeing a problem written either way. For each problem, have students estimate the difference, solve the problem using base-ten pieces, and then solve it using expanded form notation. Remind students of Math Practices Expectation 4, Check my calculations. Tell them that solving a problem two ways, first with base-ten pieces and then with expanded form, is always a good way to check calculations.

Assign the Use Expanded Form to Subtract pages in the Student Activity Book. Students will solve problems using base-ten pieces and expanded form. Some of the problems involve 1 trade.

Use Check-In: Question 5 on the Use Expanded Form to Subtract pages in the Student Activity Book to assess students’ abilities to use and apply place value concepts to make connections among representations [E1]; represent subtraction problems using base-ten pieces [E2]; subtract multidigit numbers using base-ten pieces [E3]; subtract multidigit numbers using expanded form [E4]; and estimate differences using mental math strategies [E5].

Assign the Expanded Form Subtraction Practice Homework Masters after Part 1 of this lesson.

Adventure Book:

Student Activity Book: 455 456

Answers